Leetcode 142. Linked List Cycle II

题目：

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the linked list where tail connects to. If pos is -1, then there is no cycle in the linked list.

Note: Do not modify the linked list.

 

Example 1:

Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

 

题意：

给定一个链表，他可能是存在环的，如果存在环的，找到环的起始点，如果没有环，返回null。

 

解答：

解法1   暴力解决

     一开始我的想法就是直接遍历链表，将每个节点存入hashset，只要遍历到已经在hashset中的节点，就说明是有环，并且这个重复节点就是环的开始节点。

这样的写法，可以ac，但是效率比较差

代码：

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        HashSet hs=new HashSet();
        ListNode temp=null;
        while(head!=null){
            if(hs.contains(head)) return head;
            else{
                hs.add(head);
                head=head.next;
            }
        }
        return null;
    }
}

解法2  寻找规律

这道题想要提升算法效率，需要寻找到一些规律，可以牵扯到经典的龟兔赛跑问题

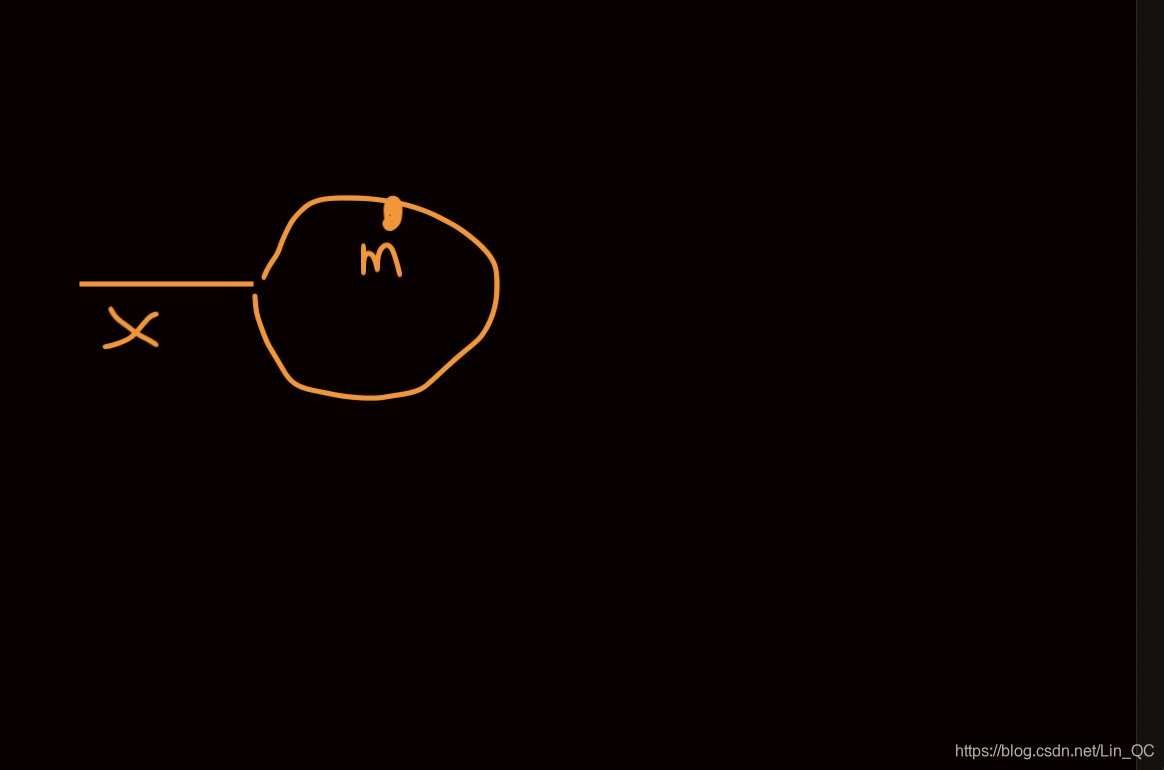
我们先假设这个链表是一个跑道，且有环。

在环开始点前，由 x 的路段

环的长度为  y  

我们设定兔子跑的比乌龟快2倍，他们同时起跑，最终在环的m处相遇（如果没有相遇，说明没有环）

那么：

兔子跑动距离为：     x+k圈*y+m

乌龟跑动距离为：     x+j 圈*y+m

 

然后我们可以得到 ：    x+k*y+m=2（x+j*y+m）

=》》》》》      可以推出     k*y= x+m+ 2*j*y

所以我们可以知道  x+m为y的倍数  也就是  x+m mod y ==0

所以我们可以知道 兔子继续走x步，他就会到环的开始点 

因为x+m会为y的倍数，那么再加x就相当于做了一个从起点出发，然后绕n圈的操作，所停的点就为环的起始点

 

这题就可以解出来了

 

代码：

 

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
            if (head == null || head.next == null) {
                return null;   // no circle
            }
            ListNode slow = head, fast = head;
            while (fast != null && fast.next != null) {
                fast = fast.next.next;
                slow = slow.next;
                if (fast == slow) {  // circle detected
                    while (head != fast) {
                        fast = fast.next;
                        head = head.next;
                    }
                    return head;
                }
            }
            return null; // no circle
    }
}