Leetcode 201. Bitwise AND of Numbers Range

最新推荐文章于 2023-12-18 09:43:22 发布

原创最新推荐文章于 2023-12-18 09:43:22 发布 · 807 阅读

0 ·

CC 4.0 BY-SA版权

算法专栏收录该内容

62 篇文章

订阅专栏

本文探讨了一道LeetCode题目，即求解一个数字区间内所有整数按位与的结果。首先介绍了错误的方法，即将区间内的所有数字存储在数组中并进行按位操作，但此方法在数据量大时会遇到内存限制问题。随后，提出了正确的解题思路，即只需比较区间的上下界以找到最长的前缀，因为后续位在按位与操作中必定为0。最后，给出了简洁高效的代码实现。

题目：

Given a range [m, n] where 0 <= m <= n <= 2147483647, return the bitwise AND of all numbers in this range, inclusive.

Example 1:

Input: [5,7]
Output: 4

Example 2:

Input: [0,1]
Output: 0

题意：给定一个数字范围，把范围内的所有整数（包括边界两个值）相与，求得到的结果

例如【5，7】

0x111

0x110

0x101

______

0x100=4

所以结果为4

解题思路：

一开始我想将范围内的数字存入到数组里，然后同时每次按位右移一位，每次移动后判断是否存在0，有的话该位直接为0，如果全为1，则该位为1

代码：

class Solution {
    public int rangeBitwiseAnd(int m, int n) {
        if(m==0) return 0;
        int []arr =new int[n-m+1];
        int level=0;
        int sum=0,yu,j;
        for(int i=0;i<=n-m;i++){
            arr[i]=m+i;
        }
        while(arr[0]!=0){
            for(j=0;j<=n-m;j++){
                yu=arr[j]%2;
                if(yu==0){
                    for(int x=j;x<=n-m;x++)
                        arr[x]=arr[x]>>1;
                    break;
                }
                arr[j]=arr[j]>>1;
                
            }
            if(j==n-m+1) sum=sum+(int)Math.pow(2,level);
            level++;
        }
        return sum;
    }
}

很遗憾的是，当范围很大时，数组大小会超出内存限制

正解思路：

其实这里面有一个规律，给定一个范围，我们只需要比较上下界的最长前缀即可（也就是对于下界从前开始最长的相同的部分），因为前缀之后的每一位，都一定会是0，1参杂的，也就是AND操作出来一定是0.

例如直接提到的【5，7】

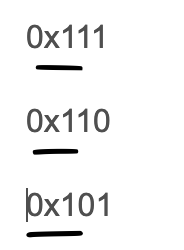
最长前缀为1，之后是00

也就是4

根据这样的思路，我们就可以将问题转化为找最长的前缀

代码：

class Solution {
    public int rangeBitwiseAnd(int m, int n) {
    int diffBits = 0;
        while (m != n) {
            m >>= 1;
            n >>= 1;
            diffBits++;
        }
        return n<<diffBits;
    }
}