Leetcode 207. Course Schedule

最新推荐文章于 2021-12-10 13:25:51 发布

原创最新推荐文章于 2021-12-10 13:25:51 发布 · 232 阅读

0 ·

CC 4.0 BY-SA版权

算法专栏收录该内容

62 篇文章

订阅专栏

博客围绕课程顺序问题展开，课程编号从0到n - 1，输入二维数组表示课程先后关系。需判断给定序列是否满足要求，即不存在矛盾。采用拓扑思维，将课程顺序转化为拓扑图，通过处理入度为0的节点来判断序列有效性，并给出了解题思路。

题目：

There are a total of n courses you have to take, labeled from 0 to n-1.

Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]

Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?

Example 1:

Input: 2, [[1,0]] 
Output: true
Explanation: There are a total of 2 courses to take. 
             To take course 1 you should have finished course 0. So it is possible.

Example 2:

Input: 2, [[1,0],[0,1]]
Output: false
Explanation: There are a total of 2 courses to take. 
             To take course 1 you should have finished course 0, and to take course 0 you should
             also have finished course 1. So it is impossible.

题意：这是一道描述上课顺序的题，课程编号为0 到 n-1，输入为一串的二维数组，【0，1】表示上0课前需要上1课。

需要求的是给定一个序列，是否可以满足要求，也就是不存在矛盾。

解法：

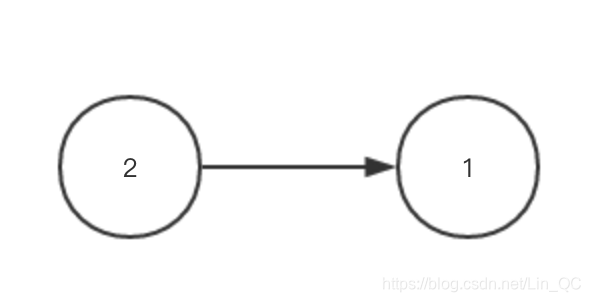
利用拓扑的思维，其实这些上课的顺序就是一个拓扑顺序，如果1要在2之前上，输入为[2,1] 那么拓扑图形化就可以表示为

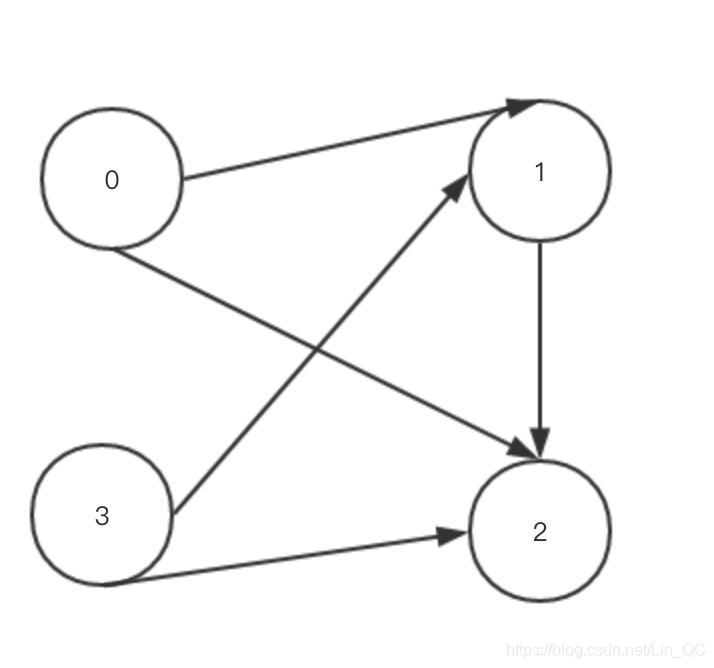
假设输入为 {[0,1],[0,2],[3,1],[3,2],[1,2]}

那么拓扑图为

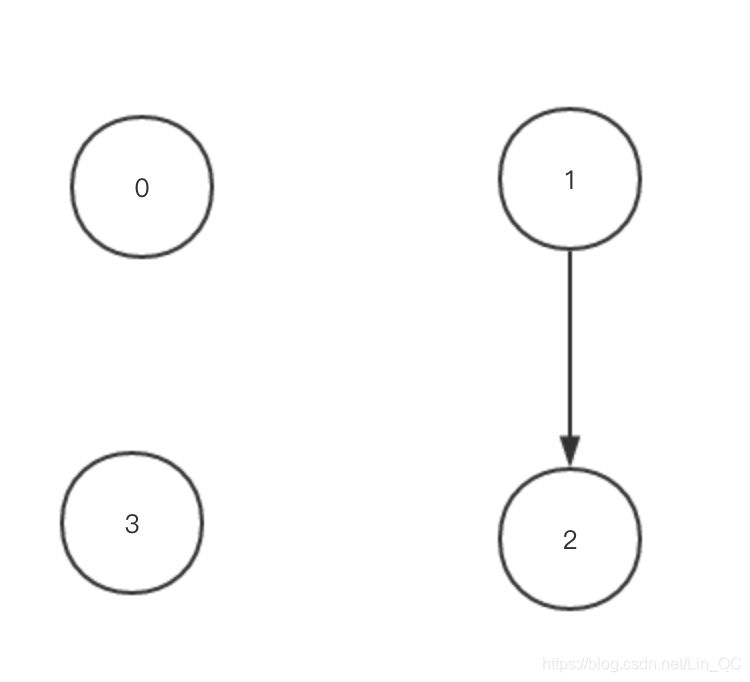
我们找到入度为0的点，消除从他们出发的连线。

更新之后，在对0度节点进行处理

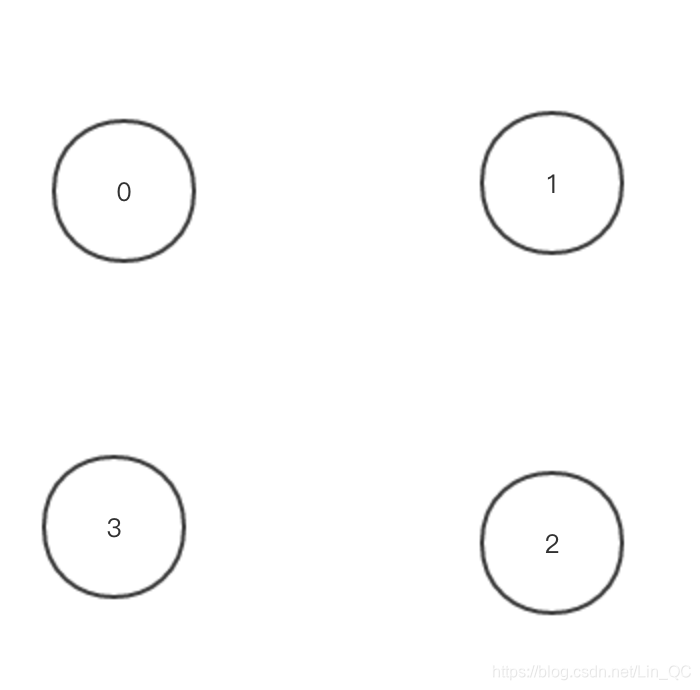
如果最后能将每个节点都化为入度为0，则说明这个序列是有效的。

代码：

class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        ArrayList[] graph = new ArrayList[numCourses];
        int[] degree = new int[numCourses];
        Queue queue = new LinkedList();
        int count=0;
        
        for(int i=0;i<numCourses;i++)
            graph[i] = new ArrayList();
            
        for(int i=0; i<prerequisites.length;i++){
            degree[prerequisites[i][1]]++;
            graph[prerequisites[i][0]].add(prerequisites[i][1]);
        }
        for(int i=0; i<degree.length;i++){
            if(degree[i] == 0){
                queue.add(i);
                count++;
            }
        }
        
        while(queue.size() != 0){
            int course = (int)queue.poll();
            for(int i=0; i<graph[course].size();i++){
                int pointer = (int)graph[course].get(i);
                degree[pointer]--;
                if(degree[pointer] == 0){
                    queue.add(pointer);
                    count++;
                }
            }
        }
        if(count == numCourses)
            return true;
        else    
            return false;
    }
}