Leetcode 78 subset 求子集_subset线代-优快云博客

本文链接：https://blog.youkuaiyun.com/Lin_QC/article/details/89186436

本文详细解析了如何使用回溯算法生成一个集合的所有可能子集，包括空集。通过实例说明了递归过程，展示了算法的具体实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目如下：

Given a set of distinct integers, nums, return all possible subsets (the power set).

Note: The solution set must not contain duplicate subsets.

Example:

Input: nums = [1,2,3]
Output:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

题意显而易见，就是要求一个集合所有的子集，包括空集。

这里我准备采用回溯算法。

主要思想是，首先计算一个元素所能组成的集合，之后计算两个元素，三个元素、、、直到全集

例如: 求三个元素的集合过程大致如下，假设集合是[1,2,3,4,5]

每次从一个节点开始，子节点的编号（注意，是编号，而不是数值大小）大于父节点

以1开始

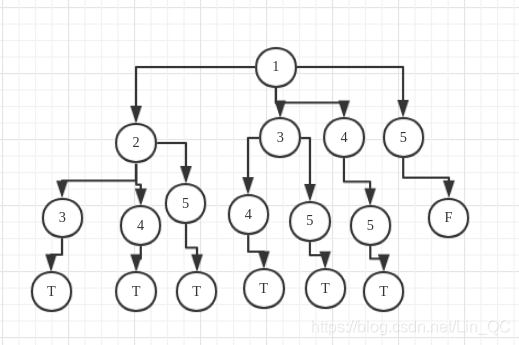
以2开始

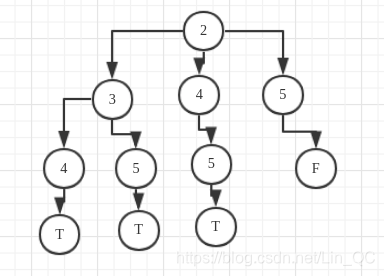
以3开始

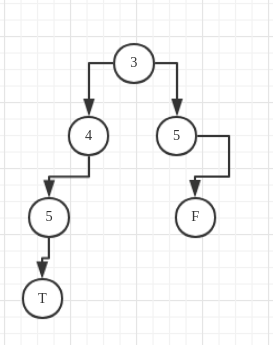
以 4,5开始

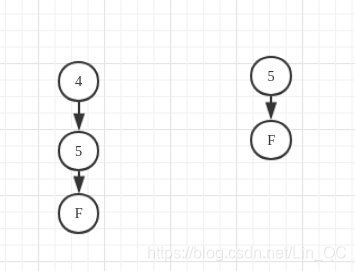
每当满足层数为3时，记录为true，保存该子集。

代码：

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> ans=new ArrayList<>();
            int len=nums.length;
            for(int i=1;i<=len;i++){
                for(int j=0;j<len;j++) {
                    List<Integer> temp=new ArrayList();
                    digui(1, j, i,temp,len,nums,ans);
                }
            }
            ans.add(new ArrayList()); //加入空集
            return ans;
    }
    public static void digui(int step,int now_location,int deep,List<Integer> temp,int len,int []nums,List<List<Integer>> ans){

        temp.add(nums[now_location]);
        if(step==deep){
            List<Integer> node=new ArrayList();
            node.addAll(temp);
            ans.add(node);
            temp.remove(step-1);
            return;
        }
        if(now_location+1<len){
            for(int i=now_location+1;i<len;i++){
                digui(step+1,i,deep,temp,len,nums,ans);
               
            }
            temp.remove(step-1);    //当本层元素都试过时，应回退一步
            return ;
        }
        else {
            temp.remove(step-1);    //回退一步
            return;
        }
    }
}