【java&algorithmStar】基于algorithmStar库进行人脸图像位置识别并介绍其原理。

原创已于 2023-04-09 21:49:26 修改 · 431 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#java #人工智能 #计算机视觉 #视觉检测

于 2023-04-04 11:35:18 首次发布

本文介绍了如何使用Java的algorithmStar库实现人脸识别，涉及人脸位置识别、度量计算（德式度量和曼哈顿度量）、图像矩阵结构以及卷积匹配。通过示例代码展示了度量计算在模板匹配中的应用，以及如何在图像上定位人脸。

前期准备

人脸识别是机器学习中常用的技术，在本次操作中我们将会使用 algorithmStar 机器学习库简易快速的搭建起来一个人脸位置识别模型，本次涉及到的知识点包含度量系数，图像矩阵的组成，图像卷积。

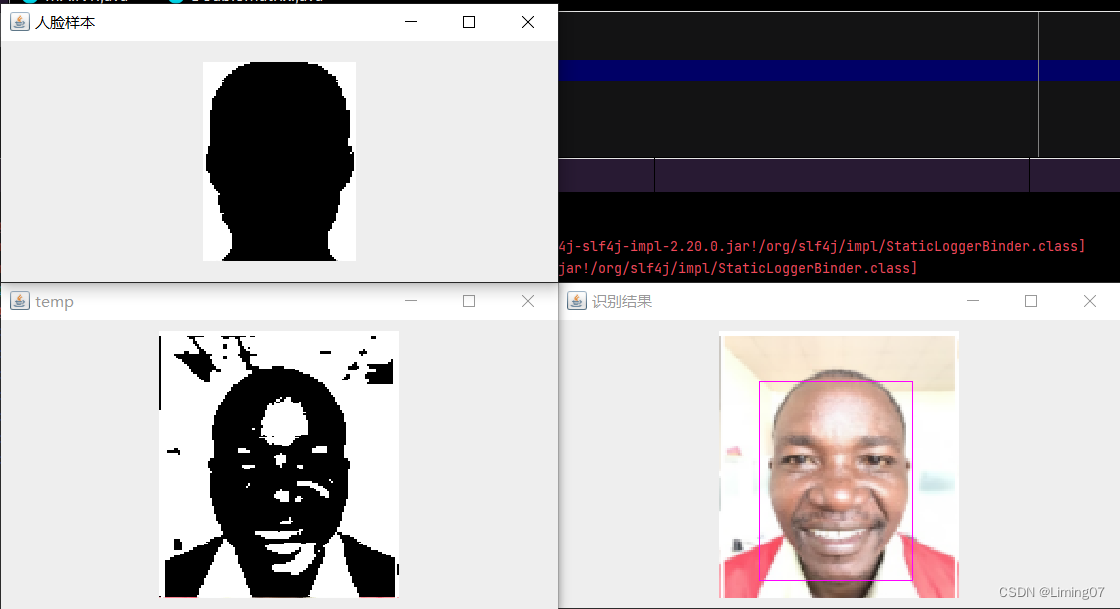
在正式开始之前需要准备一些数据，在下面展示的就是本次需要使用的数据集，首先展示的是一个是人脸轮廓样本数据，其取成年男性的人脸的平均特征构建的一个人脸轮廓样本，该样本相当于是计算机学习人脸的知识，通过该样本，计算机知道了人是什么样子。

第二个是被处理的图像矩阵，可以看到这里是一张男性的自拍照，但是对于计算机来说，它并不知道这描述的是什么，但是当样本与原图像特征的完美配合的时候，就可以发挥有趣的效果了。

人脸位置识别实现

本次演示我们将使用 Java的机器学习API algorithmStar 来进行具体的实现操作，该库的使用是很简单的，诸多复杂的计算算法被封装成为了函数，针对视觉库来说，一切操作作用于图像矩阵中，为函数式编程，具体的信息可以访问GitHub中的托管源码官网。

由于在进行人脸识别的时候，使用编程实现的步骤会过于繁琐，会导致学习难度过大，本次我们将引入一个机器学习与数据计算库来进行具体的操作，因此需要导入此库的maven依赖，具体的依赖坐标如下所示。

    <dependencies>
        <!-- algorithmStar 机器学习库的依赖坐标 -->
        <dependency>
            <groupId>io.github.BeardedManZhao</groupId>
            <artifactId>algorithmStar</artifactId>
            <version>1.18</version>
        </dependency>

        <!-- Binding using the adapter of log4j2 -->
        <dependency>
            <groupId>org.apache.logging.log4j</groupId>
            <artifactId>log4j-slf4j-impl</artifactId>
            <version>2.20.0</version>
            <!--<scope>provided</scope>-->
        </dependency>

        <!-- Log4j2 log facade -->
        <dependency>
            <groupId>org.apache.logging.log4j</groupId>
            <artifactId>log4j-api</artifactId>
            <version>2.20.0</version>
            <!--<scope>provided</scope>-->
        </dependency>
        <!-- Log4j2 log real surface -->
        <dependency>
            <groupId>org.apache.logging.log4j</groupId>
            <artifactId>log4j-core</artifactId>
            <version>2.20.0</version>
            <!--<scope>provided</scope>-->
        </dependency>
    </dependencies>

度量计算介绍

度量计算，通常用来描述向量或矩阵之间的数据差异，其代表的是两个对象之间的距离数值，针对某些计算算法来说，计算出来的度量系数越大，差异越大，例如曼哈顿等，而对于某些计算算法来说，度量系数于差异成反相关，例如余弦距离计算，在这里主要介绍两个常用的度量计算组件，德式度量和曼哈顿度量。

德式度量计算

德式度量描述的是两个多维序列之间的直线距离，其更适合用来计算最短距离，但是其计算算法中包含平方计算，导致如果序列中的数值过大过多的时候会发生超大计算量以及精度溢出的问题，下面就是德式度量的数学表示，其中x1与x2代表两个需要被计算度量的坐标，向量或矩阵序列对象，n代表序列对象中的元素编号。

$\large f(x1, x2) = \sqrt{ \sum (x1_{n})^{2} - (x2_{n})^{2}}$

接下来就是德式距离的图解展示，其描述的是两个坐标之间的直线距离。

曼哈顿度量计算

曼哈顿度量计算描述的是两个多维序列之间的道路街区距离，其不是直线，而是沿着某些坐标一段一段的移动，最终会计算出曼哈顿距离，这种距离只能移动执教，而不能移动对角线，其计算公式与图解图如下所展示。

$\large f(x1, x2) = \sum \left | x1_{n} - x2_{n} \right |$

德式度量与曼哈顿度量计算

在这里我们将会使用 AS 库进行一个简单的矩阵相似度度量系数计算，来让各位更加理解度量计算的用途。

首先我们示例化出来三个矩阵对象A B C，其A矩阵与B矩阵对象中的元素是一致的，A矩阵与C矩阵中的元素是不一致的，接下来我们将使用德式度量与曼哈顿计算A与B，A与C之间的度量系数数值，并将其进行对比，突出度量计算的效果。

创建出来矩阵对象

package zhao.algorithmMagic;

import zhao.algorithmMagic.operands.matrix.DoubleMatrix;


public class MAIN1 {
    public static void main(String[] args) throws CloneNotSupportedException {
        // 手动实例化出来 A B C三个矩阵
        DoubleMatrix matrixA = DoubleMatrix.parse(
                new double[]{1, 2, 3, 4, 5},
                new double[]{6, 7, 8, 9, 0},
                new double[]{2, 4, 6, 8, 0},
                new double[]{1, 3, 5, 7, 9}
        );
        // B 矩阵中的数与A矩阵中的数据一致，因为这里是克隆出来的矩阵
        DoubleMatrix matrixB = (DoubleMatrix) matrixA.clone();
        // C 矩阵手动赋值，与A矩阵中的数据不一致
        DoubleMatrix matrixC = DoubleMatrix.parse(
                new double[]{10, 20, 30, 40, 50},
                new double[]{6, 7, 8, 9, 0},
                new double[]{2, 4, 6, 8, 0},
                new double[]{1, 3, 5, 7, 9}
        );
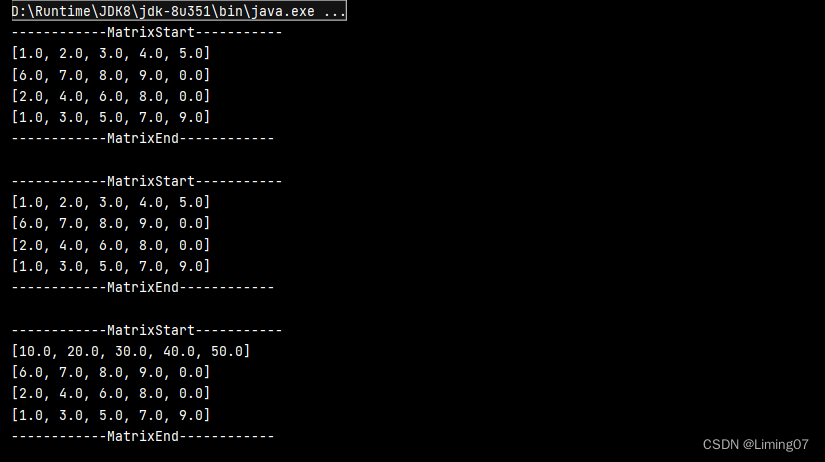
        // 打印三个矩阵中的数据
        System.out.println(matrixA);
        System.out.println(matrixB);
        System.out.println(matrixC);
    }
}

计算德氏度量

package zhao.algorithmMagic;

import zhao.algorithmMagic.algorithm.distanceAlgorithm.EuclideanMetric;
import zhao.algorithmMagic.core.AlgorithmStar;
import zhao.algorithmMagic.operands.matrix.DoubleMatrix;


public class MAIN1 {
    public static void main(String[] args) throws CloneNotSupportedException {
        // 手动实例化出来 A B C三个矩阵
        DoubleMatrix matrixA = DoubleMatrix.parse(
                new double[]{1, 2, 3, 4, 5},
                new double[]{6, 7, 8, 9, 0},
                new double[]{2, 4, 6, 8, 0},
                new double[]{1, 3, 5, 7, 9}
        );
        // B 矩阵中的数与A矩阵中的数据一致，因为这里是克隆出来的矩阵
        DoubleMatrix matrixB = (DoubleMatrix) matrixA.clone();
        // C 矩阵手动赋值，与A矩阵中的数据不一致
        DoubleMatrix matrixC = DoubleMatrix.parse(
                new double[]{10, 20, 30, 40, 50},
                new double[]{6, 7, 8, 9, 0},
                new double[]{2, 4, 6, 8, 0},
                new double[]{1, 3, 5, 7, 9}
        );
        // 获取到欧几里德计算组件
        EuclideanMetric<?, ?> euclideanMetric = EuclideanMetric.getInstance("EuclideanMetric");
        // 获取到门户对象
        AlgorithmStar<Object, Object> algorithmStar = AlgorithmStar.getInstance();
        // 计算出其中的度量数据
        System.out.println("f(A, B) = " + algorithmStar.getTrueDistance(euclideanMetric, matrixA, matrixB));
        System.out.println("f(A, C) = " + algorithmStar.getTrueDistance(euclideanMetric, matrixA, matrixC));
    }
}

计算曼哈顿度量

针对度量计算组件的更换，我们只需要将这里的实例化对象更改即可

package zhao.algorithmMagic;

import zhao.algorithmMagic.algorithm.distanceAlgorithm.ManhattanDistance;
import zhao.algorithmMagic.core.AlgorithmStar;
import zhao.algorithmMagic.operands.matrix.DoubleMatrix;


public class MAIN1 {
    public static void main(String[] args) throws CloneNotSupportedException {
        // 手动实例化出来 A B C三个矩阵
        DoubleMatrix matrixA = DoubleMatrix.parse(
                new double[]{1, 2, 3, 4, 5},
                new double[]{6, 7, 8, 9, 0},
                new double[]{2, 4, 6, 8, 0},
                new double[]{1, 3, 5, 7, 9}
        );
        // B 矩阵中的数与A矩阵中的数据一致，因为这里是克隆出来的矩阵
        DoubleMatrix matrixB = (DoubleMatrix) matrixA.clone();
        // C 矩阵手动赋值，与A矩阵中的数据不一致
        DoubleMatrix matrixC = DoubleMatrix.parse(
                new double[]{10, 20, 30, 40, 50},
                new double[]{6, 7, 8, 9, 0},
                new double[]{2, 4, 6, 8, 0},
                new double[]{1, 3, 5, 7, 9}
        );
        // 获取到欧几里德计算组件
        ManhattanDistance<?, ?> manhattanDistance = ManhattanDistance.getInstance("EuclideanMetric");
        // 获取到门户对象
        AlgorithmStar<Object, Object> algorithmStar = AlgorithmStar.getInstance();
        // 计算出其中的度量数据
        System.out.println("f(A, B) = " + algorithmStar.getTrueDistance(manhattanDistance, matrixA, matrixB));
        System.out.println("f(A, C) = " + algorithmStar.getTrueDistance(manhattanDistance, matrixA, matrixC));
    }
}

图像矩阵结构介绍

一张图像是由许多的像素构成，每一种像素具有很多的颜色，这些颜色的生成原子RGB三原色，三种颜色在不同程度上的互相搭配就形成了千种颜色，来为图像赋予生机。

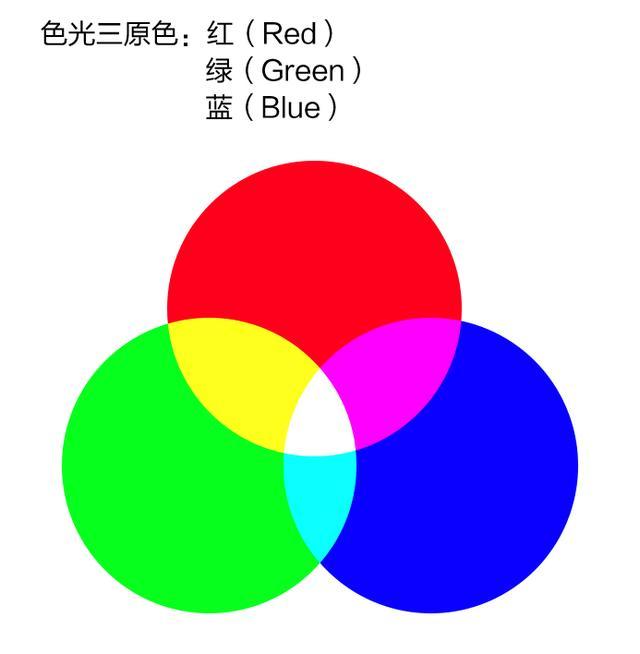
在上面我们就可以看到三种颜色的搭配可以生成不同的颜色数值，因此图像的每一个像素具有三种颜色的通道，每一个通道中存储着每一种颜色的深度数值，数值越高，代表该颜色包含的越多，因此就理解了图像的生成过程，图像的3D模型如下所示。

因此可以得出，图像是一个二维的矩阵，矩阵中的每一个元素具有三个颜色通道，这就就是图像矩阵的组成。

人脸识别代码实现

现在我们知道了图像矩阵的组成与度量计算操作，那么下面就可以开始进行矩阵的人脸识别了操作了，首先计算机并不知道图像中的某个位置是人脸，也不知道某个位置包含人脸，因此我们可以通过对图像进行卷积求度量的操作获取到与人脸样本最匹配的局部子图像矩阵，而这个子图像矩阵其就属于人脸。

图像卷积匹配

这种操作还有一个名字就是图像的模板匹配，它会通过在一定步长的卷积计算中识别到子图像中的数据，体现出不同局部内的特征数据结果，获取到我们的目标数据，需要注意的是，在图像数据中的度量计算中，由于三原色数值的值过大，因此针对欧几里德的计算会出现精度溢出等问题，因此我们使用曼哈顿算法针对相似度系数进行计算，因此卷积的计算公式如下所示，下面的min函数代表取最小值，Man代表曼哈顿计算函数，m1与m2就是需要被计算的矩阵度对象。

$\large R(m1, m2) = min(Man(m1, m2))$

相当于是将卷积时的每一个子图像与数据样本进行曼哈顿度量的计算操作，并对结果取最小曼哈顿系数，得出的就是与数据样本最近似的数值对象。

对图像进行二值化

由于图像中的颜色数值会干扰图像的匹配效果，因此在这里我们加载图像之后先将矩阵进行二值化，二值化之后的图像将只有黑白两种颜色。

开始模板匹配获取最匹配的子矩阵左上角坐标

获取到坐标之后我们就可以定位到矩形框的位置了，将其xy坐标加上人脸模板的大小就获取到了人脸的矩形右下角坐标。

开始绘制矩形框

通过左上角和右下角绘制指定颜色的矩形框，就可以定位到人脸的位置了。

package zhao.run;

import zhao.algorithmMagic.algorithm.distanceAlgorithm.ManhattanDistance;
import zhao.algorithmMagic.operands.coordinate.IntegerCoordinateTwo;
import zhao.algorithmMagic.operands.matrix.ColorMatrix;

import java.awt.*;
import java.net.MalformedURLException;
import java.net.URL;
import java.util.Map;

public class Test {
    public static void main(String[] args) throws MalformedURLException {
        // 解析人脸轮廓样本，作为模板 这里时直接使用的官方提供的人脸轮廓数据（适合明亮背景色的人脸样本）
        ColorMatrix parse = ColorMatrix.parse(
                new URL("https://user-images.githubusercontent.com/113756063/230775389-4477aad4-795c-47c2-a946-0afeadafad44.jpg")
        );
        // 从我们的文章中读取一个图像，并将其加载成图像矩阵，并且进行一个备份操作。
        ColorMatrix colorMatrix1 = ColorMatrix.parse(
                new URL("https://i-blog.csdnimg.cn/blog_migrate/dbf72e21c9c2b31b33479a929cf020b7.png")
        );
        ColorMatrix colorMatrix2 = ColorMatrix.parse(colorMatrix1.copyToNewArrays());
        // 接下来针对 colorMatrix1 对象进行二值化，用于降低颜色对于结果的影响
        colorMatrix1.localBinary(
                // 二值化计算时需要使用的颜色通道
                ColorMatrix._G_,
                // 二值化计算时，由于采取的是局部二值化，需要指定子矩阵数量，在这里指定为10
                10,
                // 当颜色大于局部阈值的时候要变更的颜色数值
                0xffffff,
                // 当颜色小于局部阈值的时候要变更的颜色数值
                0,
                // 指定二值化操作时，所有局部颜色阈值的偏置
                1
        );
        // 二值化结束就可以开始进行模板匹配了 匹配之后会返回一个最相似的矩阵的匹配系数以及左上角坐标
        Map.Entry<Double, IntegerCoordinateTwo> entry = colorMatrix1.templateMatching(
                // 指定需要进行模板匹配的算法
                ManhattanDistance.getInstance("MAN"),
                // 指定模板 也就是人脸样本数据
                parse,
                // 指定计算时使用的颜色通道
                ColorMatrix._G_,
                // 指定卷积步长，步长越大性能越高，越小精准度越高
                12,
                // 指定 相似系数 与 相似程度是否成正相关性 这里由于我们使用的时曼哈顿，因此为负相关，填 false
                false
        );
        // 获取到左上角坐标
        IntegerCoordinateTwo l = entry.getValue();
        // 计算出右下角坐标
        IntegerCoordinateTwo r = new IntegerCoordinateTwo(
                l.getX() + parse.getColCount(), l.getY() + parse.getRowCount()
        );
        // 绘制到备份的原矩阵并展示图像
        colorMatrix2.drawRectangle(l, r, new Color(255, 0, 255));
        colorMatrix2.show("image");
    }
}