图像插值

1、计算出目标像素在原图像中的位置

在图像处理时，首先需要计算出目标像素$(i,j)$在原图像中的位置$(x,y)$ （注意：原图像和目标图像的原点$(0,0)$均选择左上角。）：
$$x=\frac{srcWidth}{dstWidth}\ast i$$

$$y=\frac{srcHeight}{dstHeight}\ast j$$

例如要将$2\ast 2$的图像放大为$5\ast 5$，则目标像素$(2,3)$在原图像中的位置为：
$$x=\frac{2}{5}\ast 2=0.8$$

$$y=\frac{3}{5}\ast 2=1.2$$

2、找到临近的四个像素点

计算出的$(x,y)$一般都是浮点数，在原图像中并不存在该像素点，然后找到与它临近的四个实际存在的像素点
$$(0,1)(0,2)$$

$$(1,1)(1,2)$$

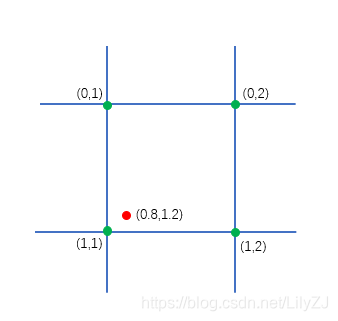
3、形式改写

将上述的$(0.8,1.2)$写成$f(u+m,v+n)$的形式，则$u=0.8,v=0.2,m=0,n=1$。

4、图像插值

（1）最近邻插值

在待求像素的四邻像素中，将距离待求像素最近的邻像素灰度赋给待求像素。

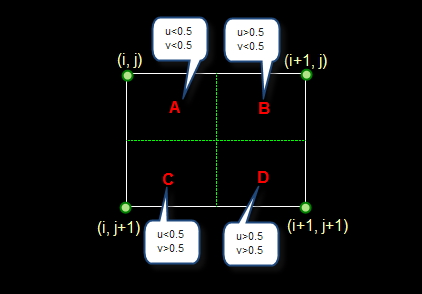
如果(i+u, j+v)落在A区，即u<0.5, v<0.5，则将左上角象素的灰度值赋给待求象素，同理，落在B区则赋予右上角的象素灰度值，落在C区则赋予左下角象素的灰度值，落在D区则赋予右下角象素的灰度值。

简单说来，就是在求得目标像素在原图像中的位置后，不是求出来有小数嘛，我们就把它四舍五入，然后在原图像中找到该位置的像素值，对应地赋给目标像素就行了。

最邻近元法计算量较小，但可能会造成插值生成的图像灰度上的不连续，在灰度变化的地方可能出现明显的锯齿状。

（2）双线性插值

双线性内插是利用待求像素四个邻像素的灰度在两个方向上作线性内插。
对于$f(u+m,v+n)$，双线性内插公式为：
$$f(u+m,v+n)=(1-u)\ast (1-v)\ast f(m,n)+(1-u)\ast v\ast f(m,n+1)+u\ast (1-v)\ast f(m+1,n)+u\ast v\ast f(m+1,n+1)$$

事实上，双线性插值基于这样一个思想，它认为某一点处的取值可以由它周围四个点的取值决定，且距离越近，决定作用越大，因此赋予一个更大的权重，这样我们利用周围四个点的值加权求和就能计算出待求像素点的值了。这里用到了四个点来计算其值，因此需要用到四个权重系数。

双线性内插法的计算比最邻近点法复杂，计算量较大，但没有灰度不连续的缺点，结果基本令人满意。它具有低通滤波性质，使高频分量受损，图像轮廓可能会有一点模糊。

（3）双三次插值

该方法利用三次多项式$S(x)$求逼近理论上最佳插值函数$sin(x)/x$，待求像素的灰度值由其周围16个灰度值加权内插得到。

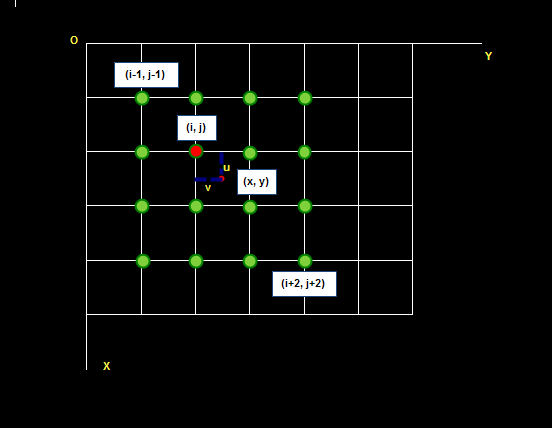
双三次插值考虑周围的16个点，因此需要16个权重系数。

三次曲线插值方法计算量较大，但插值后的图像效果最好。

参考文献：
[1] 三十分钟理解：线性插值，双线性插值Bilinear Interpolation算法
[2] 数字图像处理中的双线性插值
[3] 图像常见的插值方法
[4] 注意1：图像插值理论的理解