PAT B1013 数素数-优快云博客

本文链接：https://blog.youkuaiyun.com/Libra_69/article/details/84893976

本文详细介绍了两种有效的素数筛选算法：埃氏筛法和一般做法。埃氏筛法是一种高效算法，时间复杂度为O(nloglogn)，通过从小到大筛选非素数的倍数来获取素数。一般做法则适用于较小范围内的素数筛选，通过检查每个数是否能被小于其平方根的数整除来判断其是否为素数。文章提供了完整的C++代码实现，帮助读者理解并应用这两种算法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

令 Pi 表示第 i 个素数。现任给两个正整数 M≤N≤104，请输出 PM 到 PN 的所有素数。

输入格式：

输入在一行中给出 M 和 N，其间以空格分隔。

输出格式：

输出从 PM 到 PN 的所有素数，每 10 个数字占 1 行，其间以空格分隔，但行末不得有多余空格。

输入样例：

5 27

输出样例：

11 13 17 19 23 29 31 37 41 43
47 53 59 61 67 71 73 79 83 89
97 101 103

法一（埃氏筛法）：

埃氏筛法：是一种相对更高效的算法，其时间复杂度为O(nloglogn)

其思想是：当从小到大达到某数a，如果a没有被前面步骤的数筛去，那么a一定是素数

注意：

获取素数表时，遍历所有数时，第一个数i一定要先从2开始（不能写成 i=1,否则会导致所有输出结果都为 0），因为这是通过埃氏筛法做的，1既不是素数也不是合数（避坑，一定要避坑呀，当时一直找不出出错的地方，结果是这个出错了）
提高效率，可当得到超过n个的素数时break停止
false表示是素数

//埃氏筛法求素数表 
#include<cstdio>
const int maxn=1000001;
int prime[maxn],num=1;//num从1开始 
bool p[maxn]={0};//一开始令所有数都是素数，p[i]=flase表述i为素数
void Find_Prime(int n)
{
	for(int i=2;i<maxn;i++)//用此处i不能从1开始，否则结果全输出为0， 
	{
		if(p[i]==false)//i为素数
		{
			prime[num++]=i;
			if(num>n) break;//只需n个素数，因此超过时即可结束 
			for(int j=i+i;j<=maxn;j+=i)
			{
				p[j]=true;//筛去素数i的倍数 
			} 
		} 
	}
 }
int main(){
	int m,n;
    scanf("%d%d",&m,&n);
	Find_Prime(n);
	for(int i=m;i<=n;i++)
	{
		printf("%d",prime[i]);
		if((i-m+1)%10&&i<n) printf(" ");//到最后一个数时，题中说行末不得输出空格 
		else printf("\n");
	}
	return 0;
}

法二（一般做法）：

此方法只适用于n在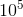 10^5 以内，其时间复杂度为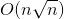 $O(n\sqrt{n})$

注意：

获取素数表时，遍历所有数时，此处可以从1开始，但最好还是不要从1开始，统一一下都从2开始
true表示是素数

//一般方法 
#include<cstdio>
#include<cmath>
const int maxn=1000001; 
int prime[maxn],num=1;//全局变量 
bool p[maxn]={0};//一开始令所有数都不是素数，p[i]=true表示是素数 
bool isPrime(int n)
{
	int sqr=(int)sqrt(1.0*n);
	for(int i=2;i<=sqr;i++)//此处i小于等于sqr
	{
		if(n%i==0) return false;
	 } 
	return true;
}
void Find_Prime(int n){
	for(int i=2;i<maxn;i++)
	{
		if(num>n) break;//break要放在循环里面 
		if(isPrime(i)==true)
		{
			prime[num++]=i;
			p[i]=true;
		}
	}
} 
int main()
{
	int m,n;
	scanf("%d%d",&m,&n);
	Find_Prime(n);
	for(int i=m;i<=n;i++)
	{
		printf("%d",prime[i]);
		if((i-m+1)%10&&i<n) printf(" ");//到最后一个数时，题中说行末不得输出空格 
		else printf("\n");
	}
	return 0;
}