信息量
I(信息量)=不确定程度的减少量
自信息量
定义:一个随机事件的自信息量定义为其出现概率对数的负值。
一个消息越不可预测,它所含的信息量就越大
(消息发生的概率越低,信息量越大)

a=2,单位为比特(bit)
信息熵(平均信息量)

大体了解概念和公式,以后再深究。
学习视频:《对话通信原理视频》
公式补充
1.
信
息
熵
1.信息熵
1.信息熵
H
(
X
)
=
E
[
−
l
o
g
2
p
(
x
i
)
]
=
∑
i
=
1
n
p
(
x
i
)
l
o
g
2
1
p
(
x
i
)
比
特
/
符
号
H(X)=E[-log_2p(x_i)]=\textstyle \sum_{i=1}^n p(x_i)log_2 \frac{1}{p(x_i)}比特/符号
H(X)=E[−log2p(xi)]=∑i=1np(xi)log2p(xi)1比特/符号
也
可
用
H
(
p
1
,
p
2
,
.
.
.
,
p
n
)
表
示
也可用H(p_1,p_2,...,p_n)表示
也可用H(p1,p2,...,pn)表示
2.
联
合
熵
2.联合熵
2.联合熵
H
(
X
,
Y
)
=
∑
i
=
1
n
∑
j
=
1
n
p
(
x
i
,
y
j
)
l
o
g
2
1
p
(
x
i
,
y
j
)
比
特
/
符
号
对
H(X,Y)=\textstyle \sum_{i=1}^n \sum_{j=1}^n p(x_i,y_j)log_2 \frac{1}{p(x_i,y_j)} 比特/符号对
H(X,Y)=∑i=1n∑j=1np(xi,yj)log2p(xi,yj)1比特/符号对
3.
条
件
熵
3.条件熵
3.条件熵
H
(
Y
∣
X
)
=
∑
i
=
1
n
p
(
x
i
)
H
(
Y
∣
x
i
)
=
∑
i
=
1
n
∑
j
=
1
n
p
(
x
i
,
y
j
)
l
o
g
2
1
p
(
y
j
∣
x
i
)
比
特
/
符
号
对
H(Y|X)=\textstyle \sum_{i=1}^n p(x_i)H(Y|x_i)=\textstyle \sum_{i=1}^n \sum_{j=1}^n p(x_i,y_j)log_2 \frac{1}{p(y_j|x_i)} 比特/符号对
H(Y∣X)=∑i=1np(xi)H(Y∣xi)=∑i=1n∑j=1np(xi,yj)log2p(yj∣xi)1比特/符号对
4.
互
信
息
4.互信息
4.互信息
I
(
X
;
Y
)
=
H
(
X
)
−
H
(
X
∣
Y
)
=
H
(
Y
)
−
H
(
Y
∣
X
)
=
H
(
X
)
+
H
(
Y
)
−
H
(
X
,
Y
)
比
特
/
符
号
对
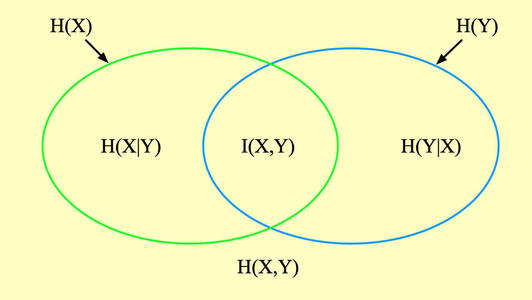
I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)=H(X)+H(Y)-H(X,Y)比特/符号对
I(X;Y)=H(X)−H(X∣Y)=H(Y)−H(Y∣X)=H(X)+H(Y)−H(X,Y)比特/符号对
5.
基
本
性
质
5.基本性质
5.基本性质
- 非负性:由定义可得
- 对称性:当概率矢量中的各分量的次序任意变更时,熵值不变。
- 确定性:某消息取值概率为1时,熵为0
- 极值性:等概时取得极大值
H ( p 1 , p 2 , . . . , p n ) ≤ H ( 1 n , 1 n , . . . , 1 n ) = l o g 2 n H(p_1,p_2,...,p_n)≤H(\frac{1}{n},\frac{1}{n},...,\frac{1}{n})=log_2n H(p1,p2,...,pn)≤H(n1,n1,...,n1)=log2n
























 613
613

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








