【计算机组成原理】第二章 运算方法和运算器

系列文章目录

第一章 计算系统概论
第二章 运算方法和运算器
第三章 多层次的存储器
第四章 指令系统
第五章 中央处理器
第六章 总线系统
第七章 外围设备
第八章 输入输出系统

---

---

前言

---

【 第二章 运算方法和运算器 】

2.1 数据与文字的表示

• 计算机中使用的数据可分成两大类：
  • 符号数据:非数字符号的表示（ASCII、汉字、图形等）
  • 数值数据:数字数据的表示方式（定点、浮点）
• 计算机数字和字符的表示方法应有利于数据的存储、加工(处理)、传送；
• 编码：用少量、简单的基本符号，选择合适的规则表示尽量多的信息，同时利于信息处理（速度、方便）

2.1.1数据格式

一、定点表示法

• 所有数据的小数点位置固定不变
• 理论上位置可以任意，但实际上将数据表示有两种方法： 纯小数、纯整数
• 定点纯小数：
  
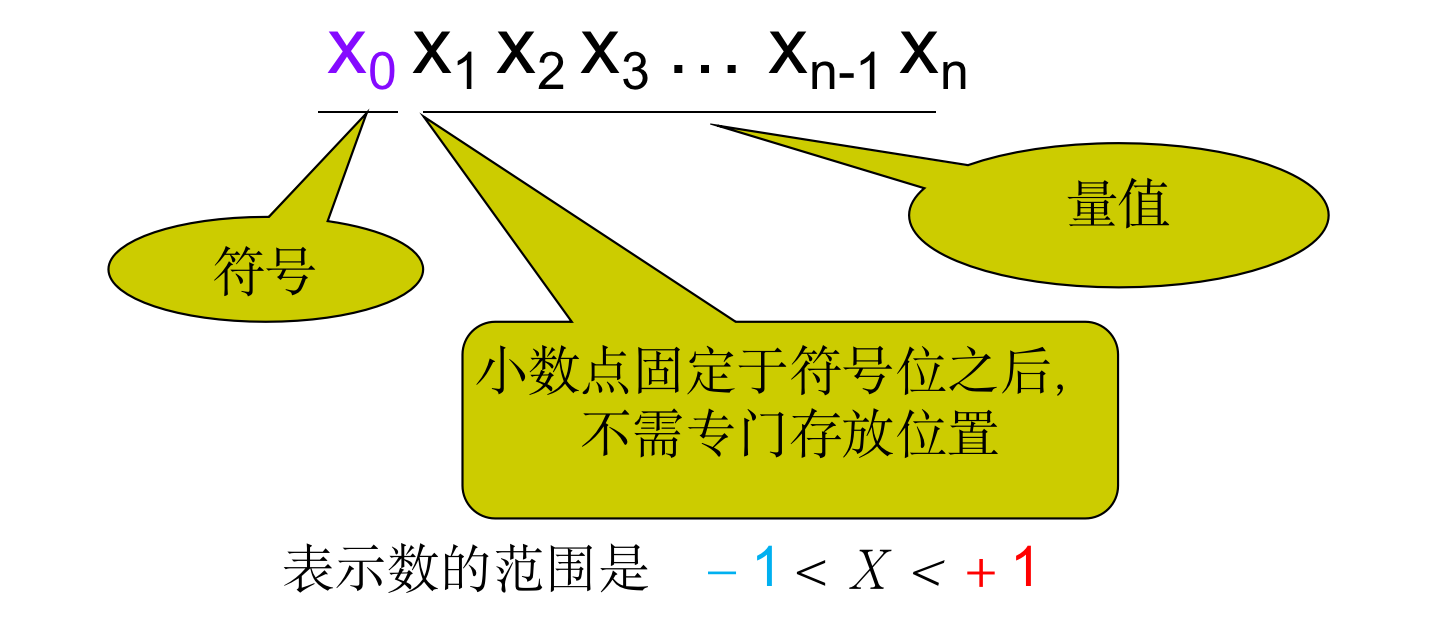
  • 纯小数表示范围
    
• 定点纯整数：
  
• 定点表示法的特点
  • 定点数表示数的范围受字长限制，表示数的范围有限;
  • 定点表示的精度有限
  • 机器中，常用定点纯整数表示;
    

2、浮点表示法：数点位置随阶码不同而浮动

• 格式:N=RE.M
  
• 机器中表示
  
• 浮点数规格化表示：
  

3、IEEE754标准(规定了浮点数的表示格式,运算规则等)

• 规则规定了单精度(32)和双精度(64)的基本格式.
• 规则中,尾数用原码,指数用移码(便于对阶和比较)
  
  
• IEEE754标准
  • 基数R=2，基数固定，采用隐含方式来表示它。
  • 32位的浮点数：
    • S数的符号位，1位，在最高位，“0”表示正数，“1”表示负数。
    • M是尾数， 23位，在低位部分，采用纯小数表示
    • E是阶码，8位，采用移码表示。移码比较大小方便。
    • 规格化： 若不对浮点数的表示作出明确规定，同一个浮点数的表示就不是惟一的。
      • 尾数域最左位(最高有效位)总是1， 故这一位经常不予存储，而认为隐藏在小数点的左边。
      • 采用这种方式时，将浮点数的指数真值e变成阶码E时，应将指数e加上一个固定的偏移值127(01111111)，即E=e+127。
• 64位的浮点数中符号位1位，阶码域11位，尾数域52位，指数偏移值是1023。因此规格化的64位浮点数x的真值为：
  • x=(-1)^S×(1.M)×2^E-1023
  • e=E-1023
• 一个规格化的32位浮点数x的真值表示为
  • x=(-1)^S×(1.M)×2^E-127
  • e=E-127
• 真值x为零表示：当阶码E为全0且尾数M也为全0时的值，结合符号位S为0或1，有正零和负零之分。
• 真值x为无穷大表示：当阶码E为全1且尾数M为全0时，结合符号位S为0或1，也有+∞和-∞之分。
• 这样在32位浮点数表示中，要除去E用全0和全1（25510）表示零和无穷大的特殊情况，指数的偏移值不选128（10000000），而选127（01111111）。对于规格化浮点数，E的范围变为1到254，真正的指数值e则为-126到+127。因此32位浮点数表示的绝对值的范围是10-38～1038（以10的幂表示）。
• 浮点数所表示的范围远比定点数大。一台计算机中究竟采用定点表示还是浮点表示，要根据计算机的使用条件来确定。一般在高档微机以上的计算机中同时采用定点、浮点表示，由使用者进行选择。而单片机中多采用定点表示。
• 浮点数表示范围：
  

2.1.2数的机器码表示

• 真值:一般书写的数
• 机器码:为了处理符号位如何表示、是否同数值一起计算等问题，将符号位与数值位一起编码来表示相应的数。
  • 原码、反码、补码、移码

1、原码表示法

• 定点小数x0. x1x2…xn
  
• 定点整数X₀X₁X₂…X_n
  
• 原码特点：
  • 表示简单，实现乘除运算规则简单。
  • 进行加减运算十分麻烦 P20。

2、补码表示法

• 生活例子：现为北京时间下午4点，但钟表显示为7点。有两种办法校对：
  • 做减法 7-3 = 4 (逆时针退3格)
  • 做加法 7+9 = 16 (顺时针进9格)16 (mod 12) = 16-12 = 4 (以12为模，变成4)
• 定义：正数的补码就是正数的本身，负数的补码是原负数加上模。
• 计算机运算受字长限制,属于有模运算.
  • 定点小数x₀.x₁x₂…x_n，以2为模
  • 定点整数x₀.x₁x₂…x_n，以2ⁿ⁺¹为模
• 定点小数x₀.x₁x₂…x_n