JAVA基础学习——Day8（数组题目练习）

一、 Day7复习

1. 数组是引用数据类型

2. 引用类型保存的是一块堆内存的地址(对象的地址，对于数组来说是首地址)，引用其实是对象的一个别名

3. Java中使用关键字new出来的是对象，new出来的对象统一在堆内存中保存

4. 数组下标称为元素的偏移量(相对于数组首元素的偏移量)，这就是为什么第一个元素的下标为0（因为第一个元素相对于自己的偏移量为0）

5. 引用数据类型的默认值为null，表示该引用没有保存任何实际的地址值。当一个引用保存的值为null，无法通过该引用读写内存，若访问，则抛出一个NPE（空指针异常）

6. JVM内存管理中的栈区和堆区

(1)栈区：方法的调用和执行结束对应一个栈帧的入栈和出栈，方法中的所有局部变量(临时变量和形参)都保存在对应方法的栈帧之中存储，随着方法的执行结束，所有局部变量都会被销毁

(2)堆区：存储new关键字产生的对象

二、作业部分

例题1：

 

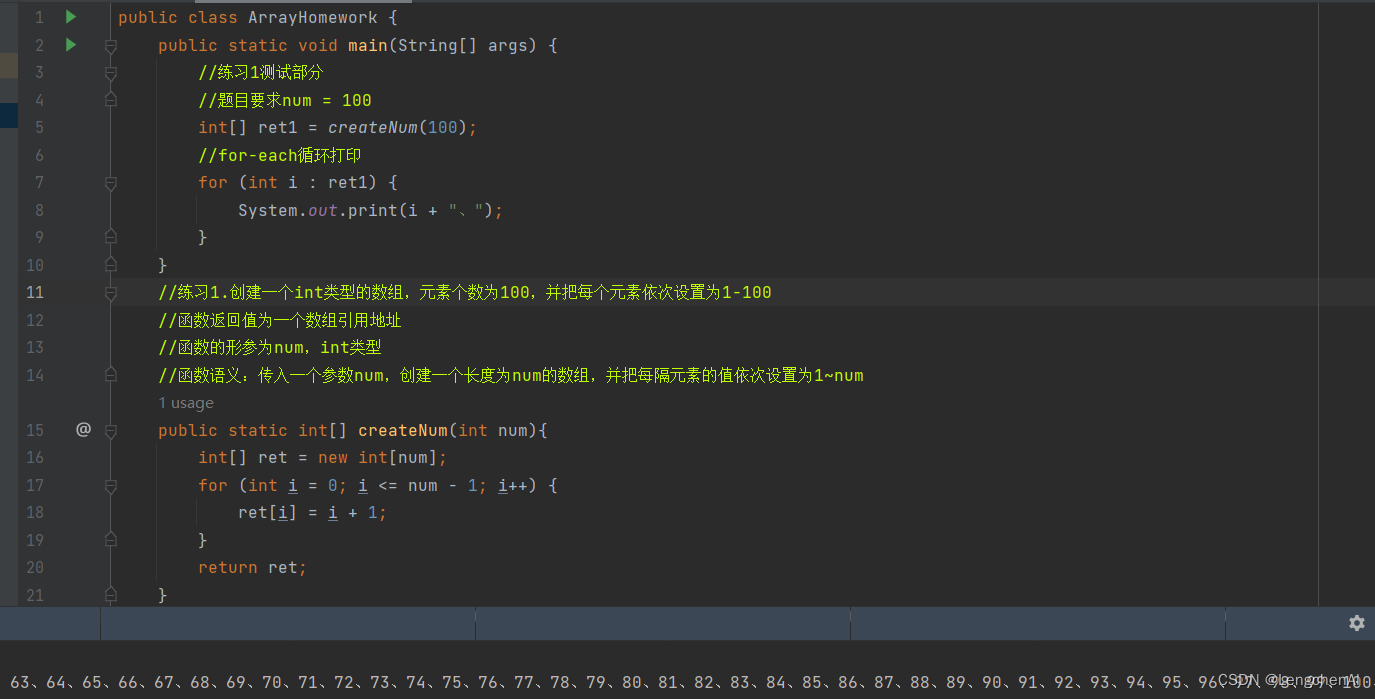
 例题2：

 

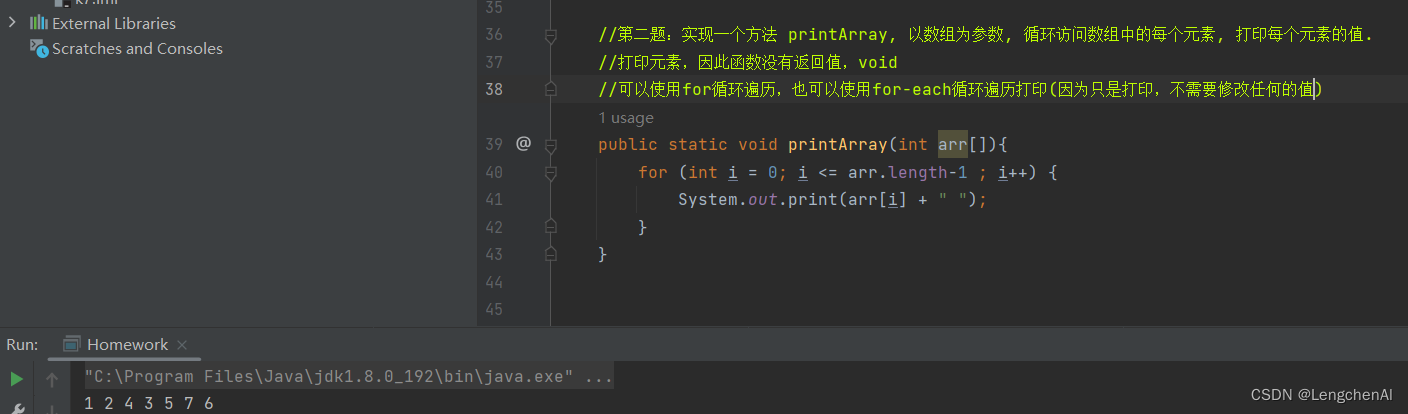
例题3： 

 

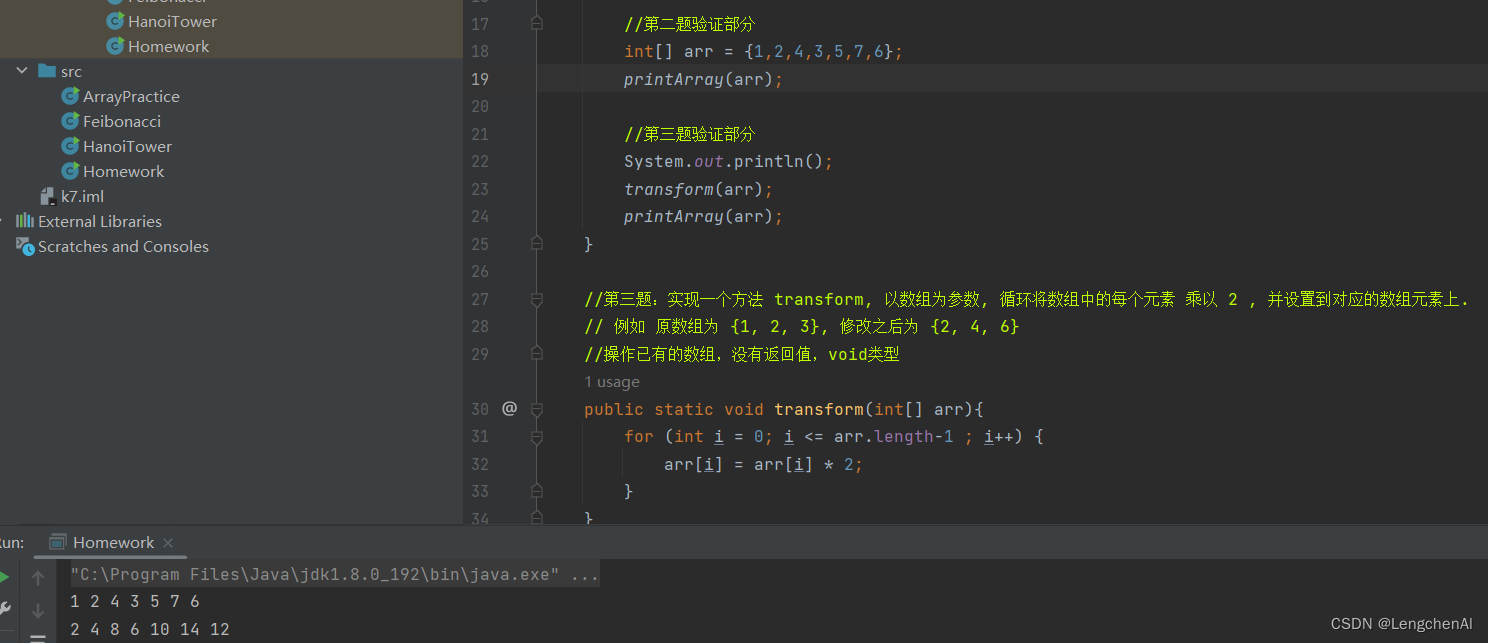
例题4：

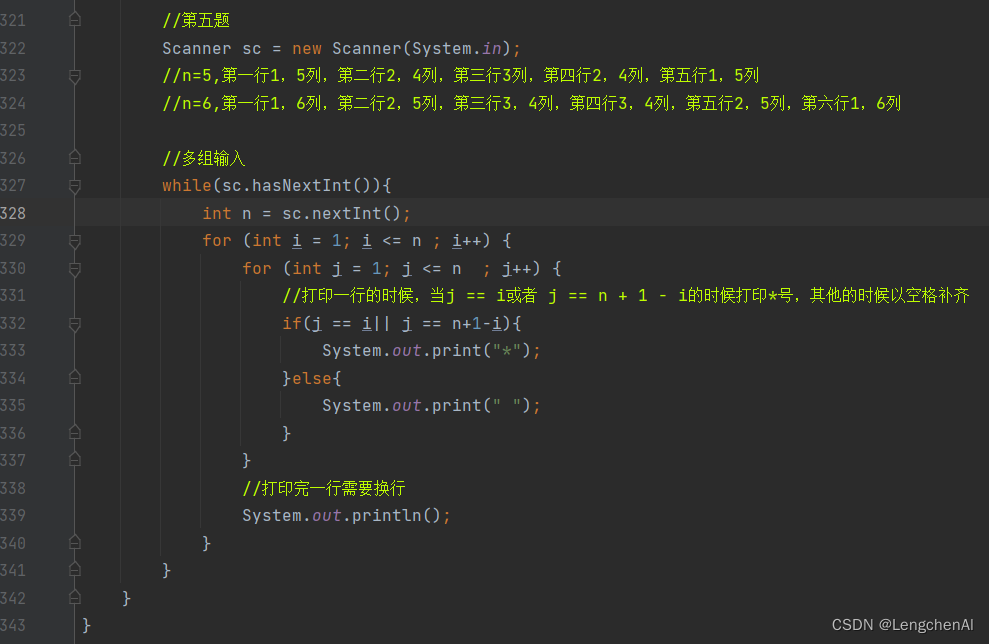
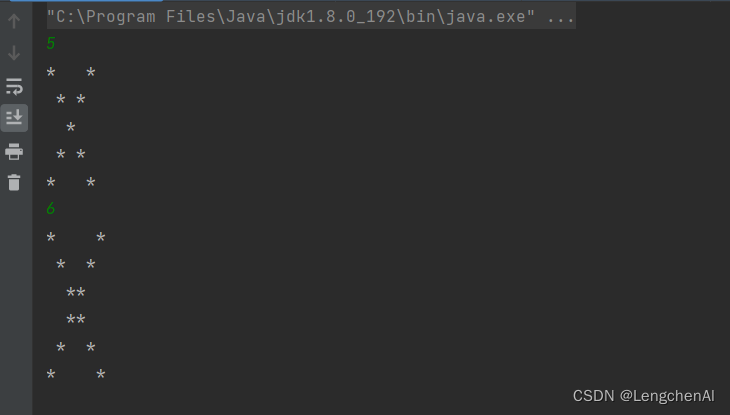
 注意：多组输入的标准格式

Scanner sc = new Scanner(System.in);

while(sc.hasNextInt){

        int n = sc.nextInt();

        .....

}

 三、数组练习题

 (1)直接打印引用数据类型，返回的不是其内容

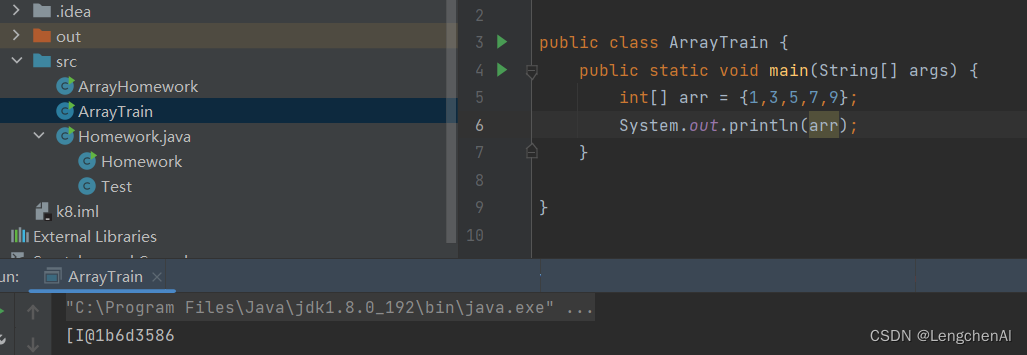
 [：表示此时的引用类型是一个数组

I：表示是一个int类型的数组

@后面的是加密后的地址

(2)要想输出数组的内容，最常用的操作是将数组转为字符串，然后再打印字符串即可。

(3)方案1：通过Arrays(数组相关的工具类)的toString方法转换

A. 语法：

//将arr数组中的内容转换为字符串对象

String ret = Arrays.toString(arr);

B. 例子

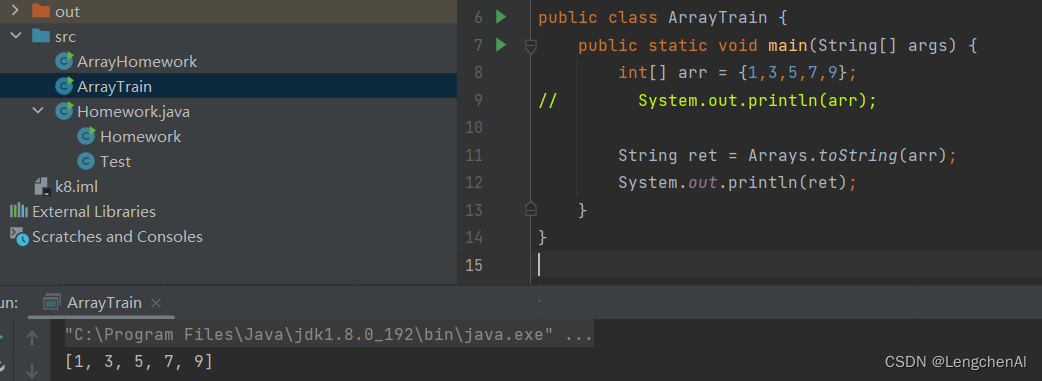
 (4) 方案二：自定义一个打印函数

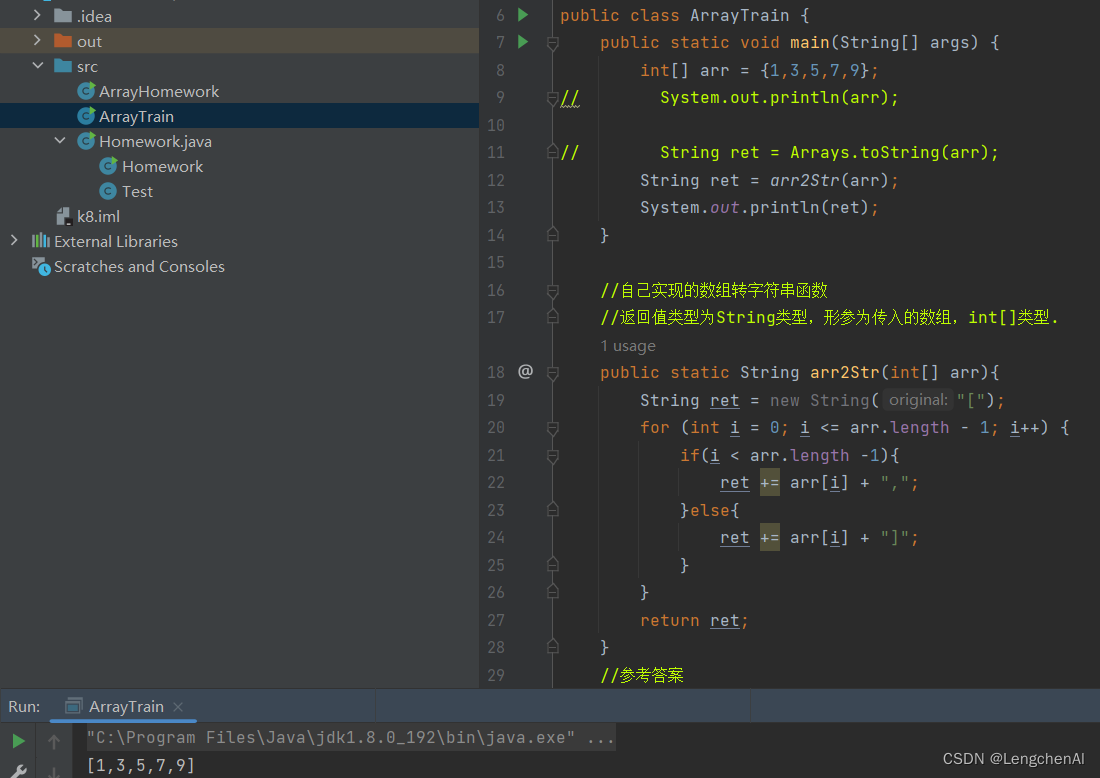
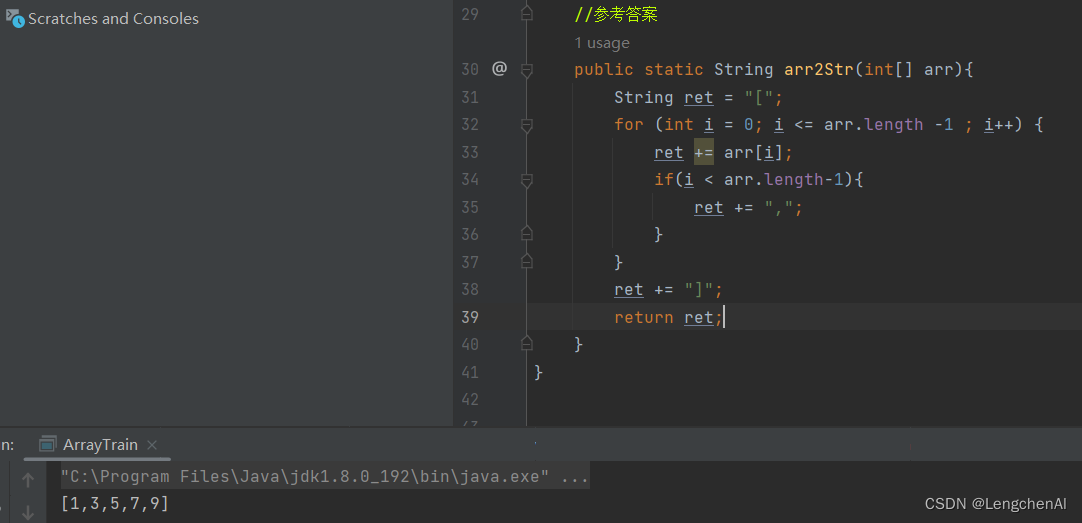
注意：String类型的两种创建和初始化

 

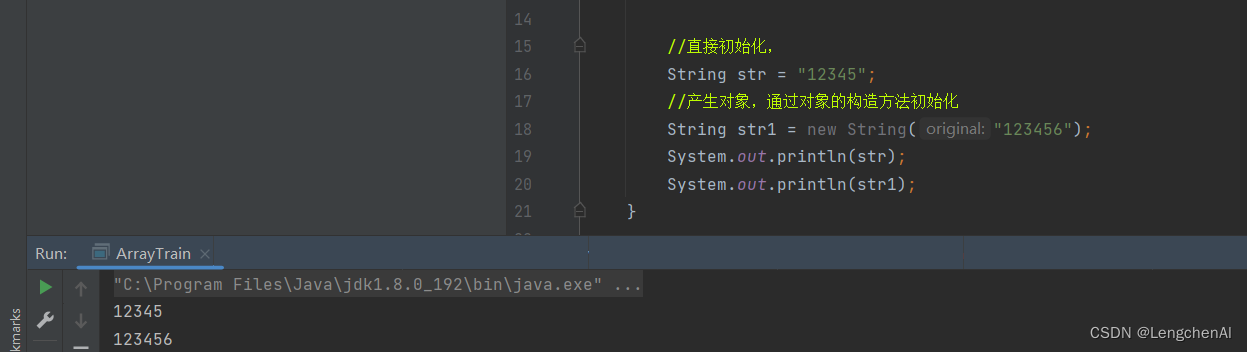
编译器编译后文件：

 (5)补充知识：

 

 

(1)数组的引用不是拷贝(没有产生新的对象，只是多了一个引用或者说是别名) 

证明代码：修改arr数组的值，发现newArr的值变了

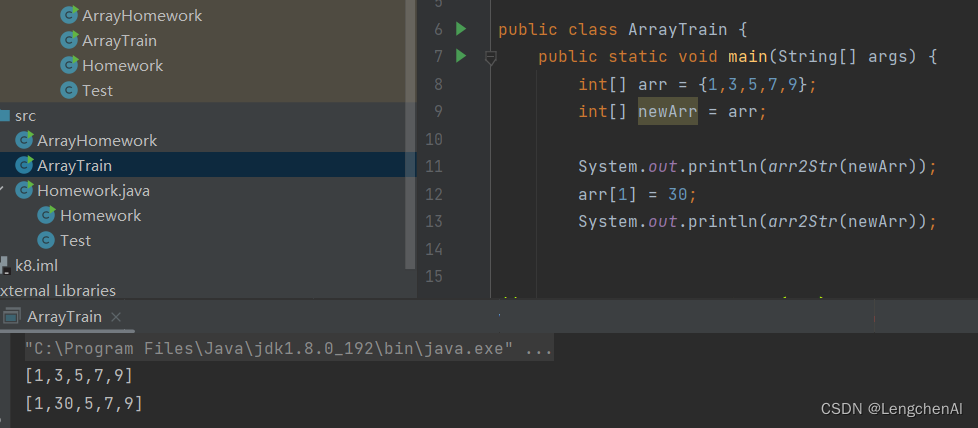
(2)什么是数组拷贝：创建一个新的数组对象，新的数组对象的内容和原数组保持一致

 (3)数组拷贝实现方案一：使用JDK中Arrays工具类中的copyOf()方法拷贝数组

A. 语法：

int[] 新数组名称 = Arrays.copyOf(原数组名称，新数组长度)；

B. 实际代码

a. 全拷贝(新数组长度 = 旧数组长度)

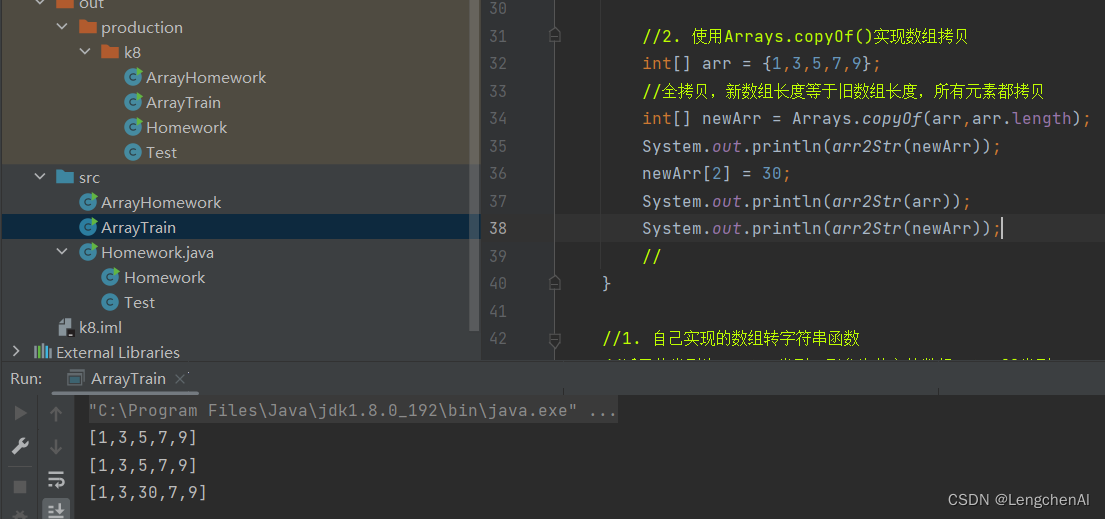
 b. 新数组长度 > 旧数组长度

 

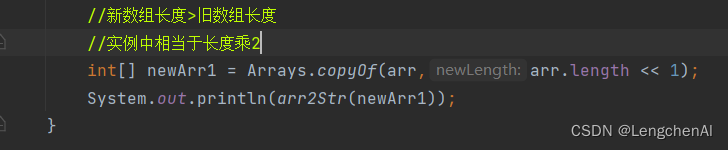
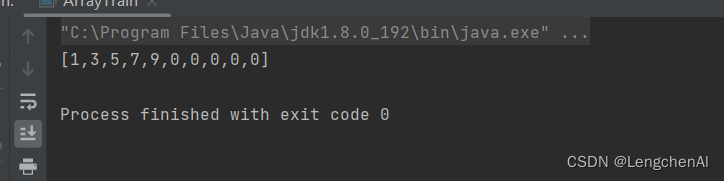
c. 新数组长度 < 旧数组长度

C. 原理总结

D. 补充知识： Arrays.copyOfRange()的用法

a. Arrays.copyOfRange()的语法

b. 代码实例

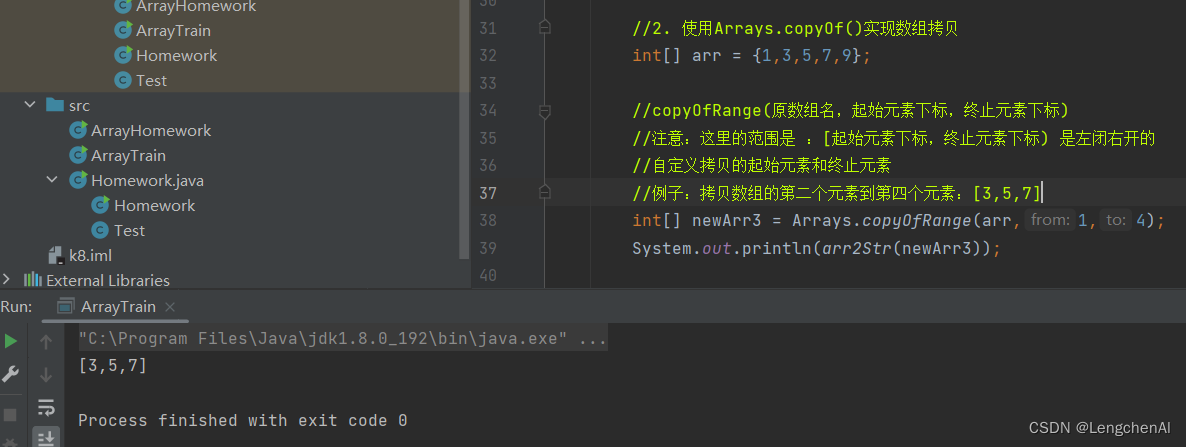
(4)数组拷贝实现方案二：定义实现的全拷贝函数

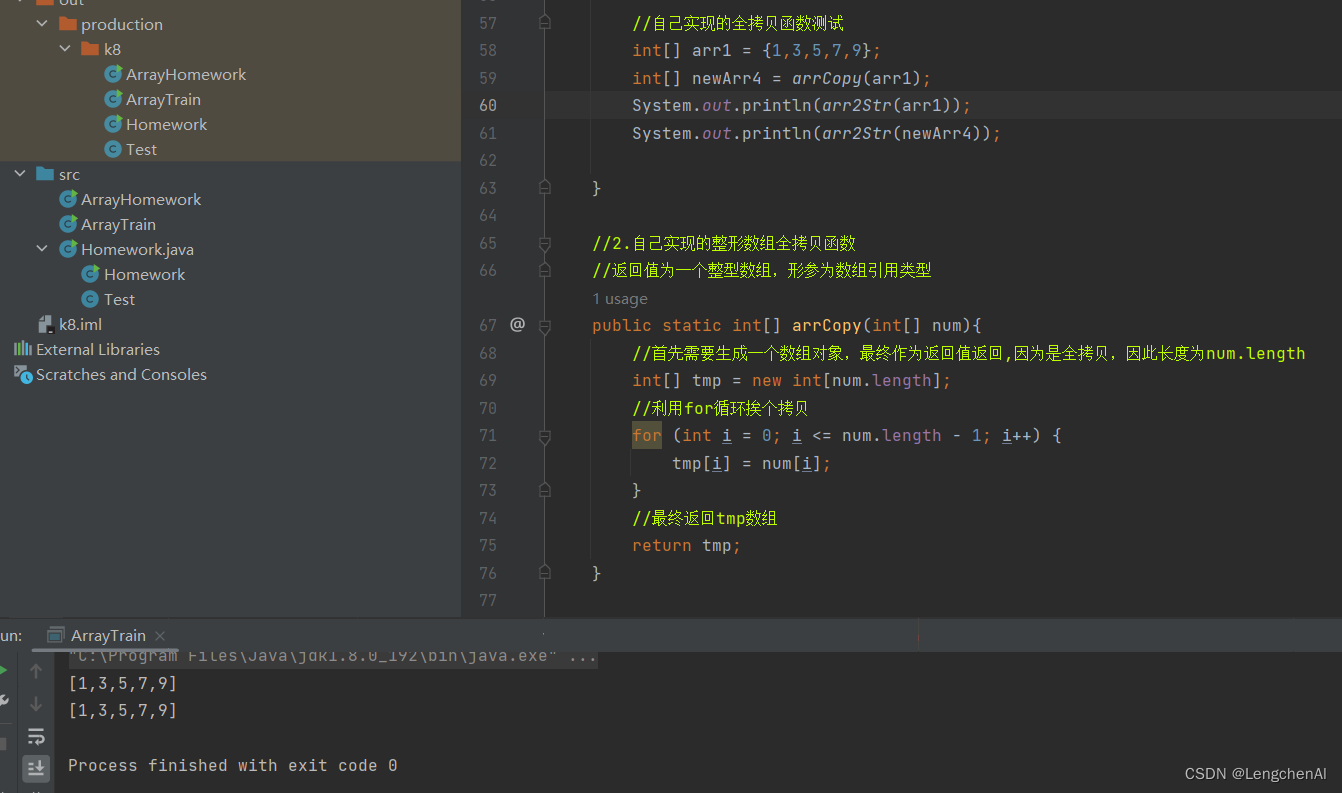
(1)代码实现

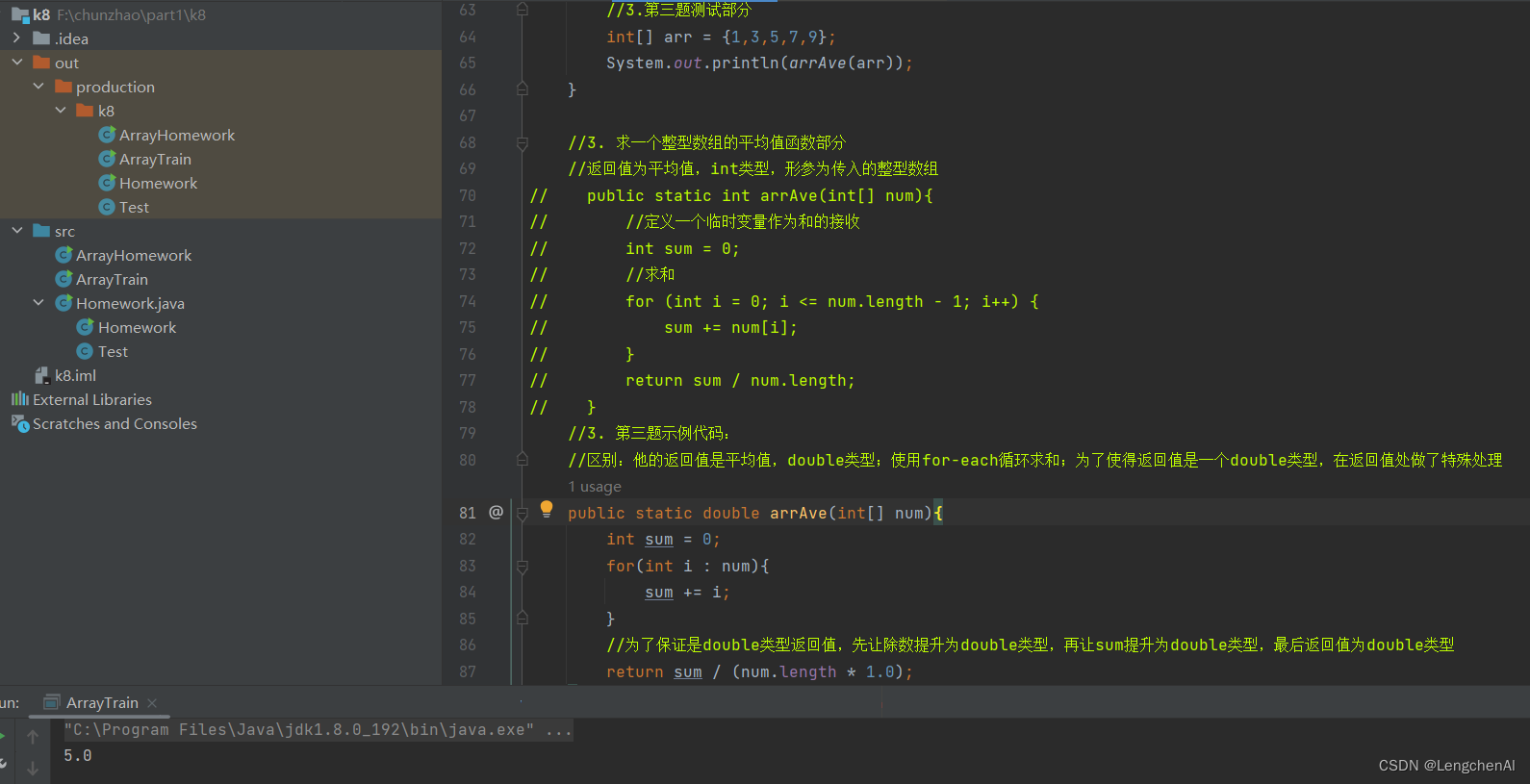
(2) 一个额外训练：数组各个元素求和(递归思路)

A. 思路：

注意：这里的索引理解为指向元素的地址更加好理解一些

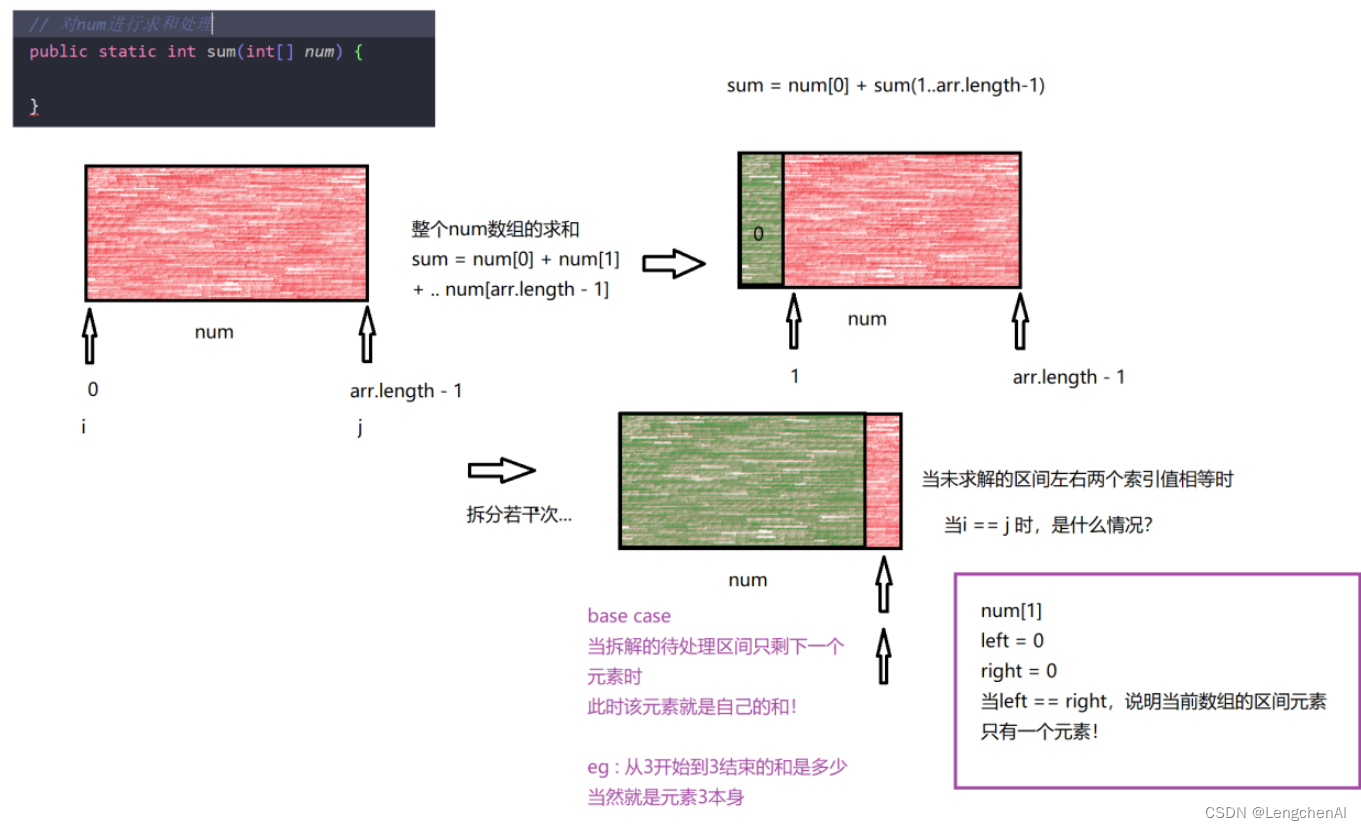
B. 代码实现与测试

 

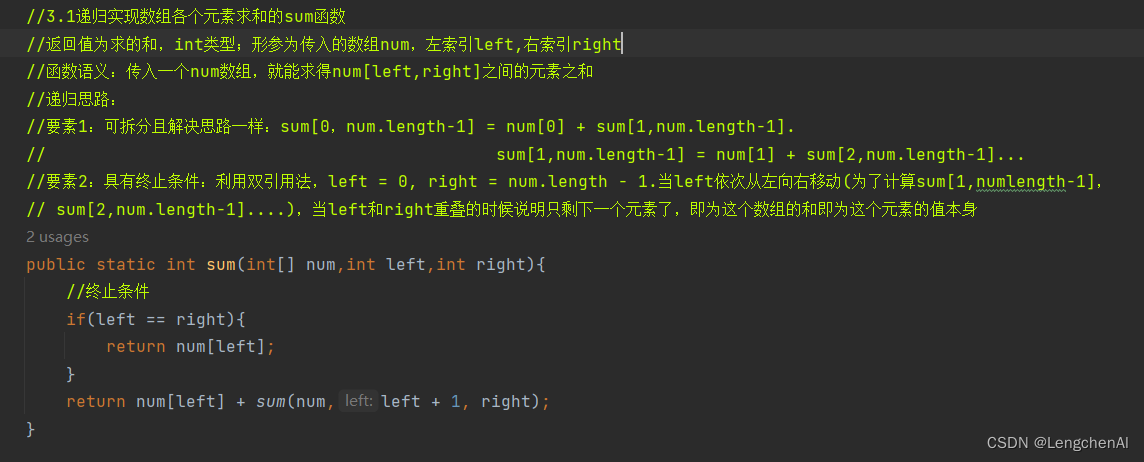
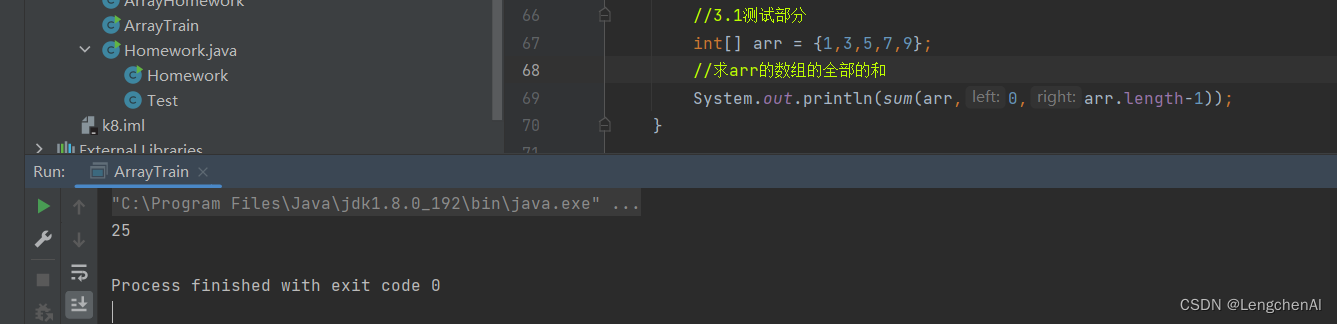
 (1)顺序查找(O(n)级别的时间复杂度)

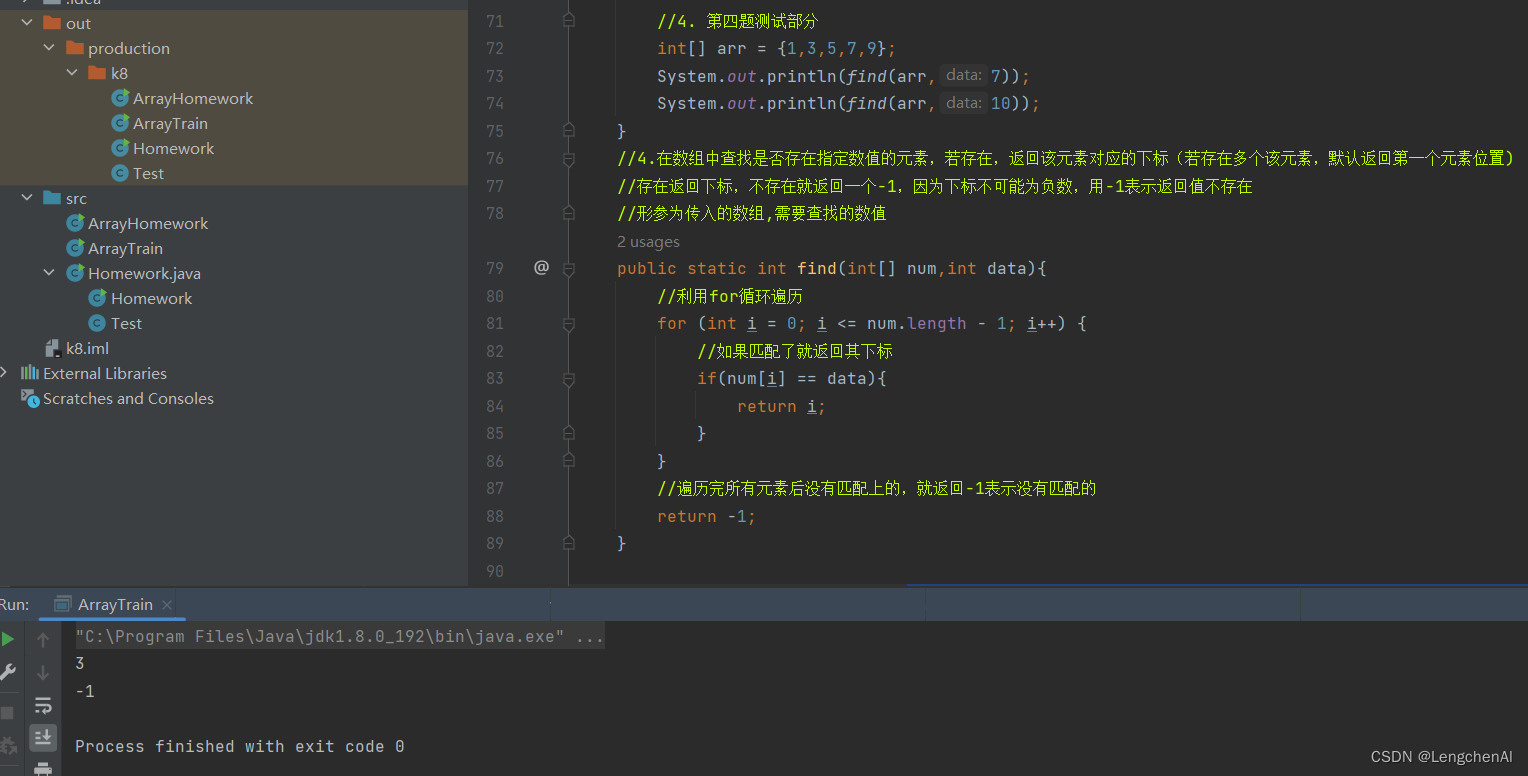(2)二分查找（O(logn)基本的时间复杂度）

 A. 二分查找适用条件：有序数组中，使用二分查找来定位一个元素是否存在

补充知识：有序数组（不考虑重复元素）

升序：数组内的所有元素均满足前一个元素小于后一个元素，eg:{1，3，5，7，9}

降序：数组内的所有元素均满足前一个元素大于后一个元素，eg:{9, 7, 5, 3, 1}

B.二分查找思想(以升序数组为例，降序数组思路类似)：

a. 定义：待查找数组定义为num, 待查找元素值为data，区间的中间位置的下标为mid(注意：这个中间位置的求解方式统一为：)

b. 思想：每次将待查找元素data和num[mid]比较

若data < num[mid],则待查找元素一定小于mid之后的元素(mid的右半区间包括mid可以直接忽略，继续在mid的左半区间寻找待查找的值)

若data > num[mid],则待查找元素一定大于mid之前的元素(mid的左半区间包括mid可以直接忽略，继续在mid的右半区间寻找待查找的值)

若data = num[mid],则找到该元素

一直采用此思路在整个数组上循环处理！

c. 图文例子演示思想

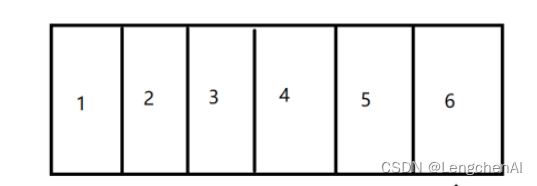
假设待查找元素data = 2

第一轮：

left = 0, right = 5

mid = left + (right - left) >> 1 = 2(注意：右移后的数值向下取整)

 data<num[2] (3)

则令righ = mid - 1 = 1；

第二轮：

mid = left + (right - left) >> 1 = 0

data>num[0] (1)

left = mid + 1 = 1 = right

此时判断num [left] == data，搜索成功，return结束返回下标left

假设带查找元素data = 10

第一轮：
left = 0,right = 5

mid = left + (right - left) >> 1 = 2

data  > num[2](3)

令left = mid + 1 = 3；

第二轮：

mid = left + (right - left) >> 1 = 3 + 1 = 4

data > num[4](5)

令left = mid + 1 = 5 = right，此时发现data != num[5]  

left = mid + 1 = 6 > right（注意：当left > right的时候则说明待搜索的区间内一个元素都没有，此时说明搜索失败，退出循环）

C.  代码实现

a. 循环实现

 

 

 

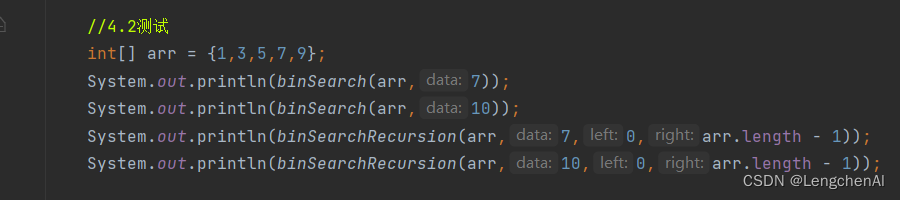
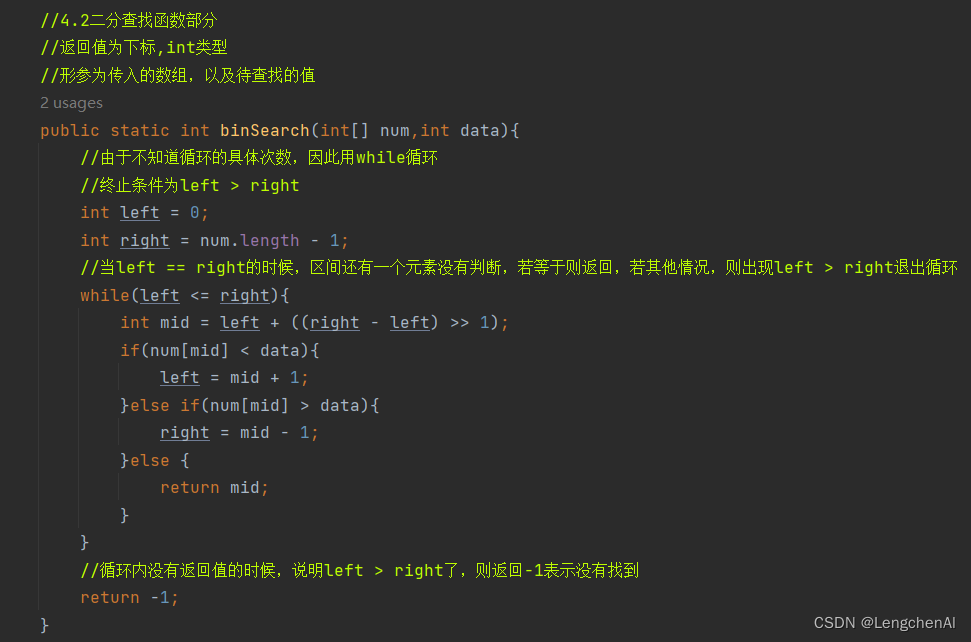
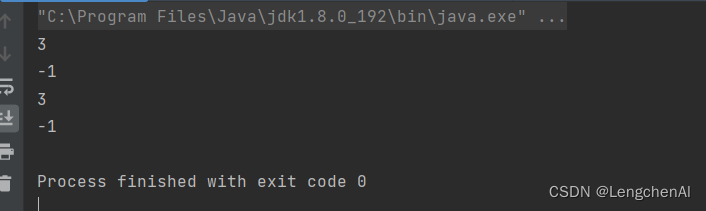
b. 递归实现

 

 

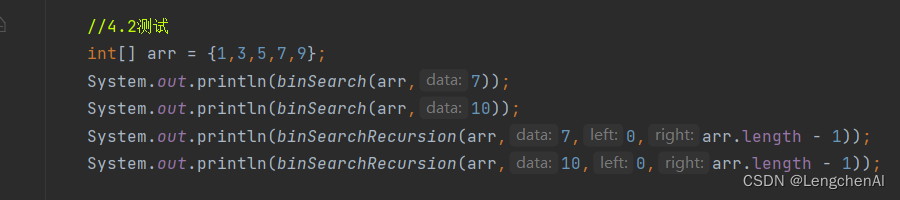
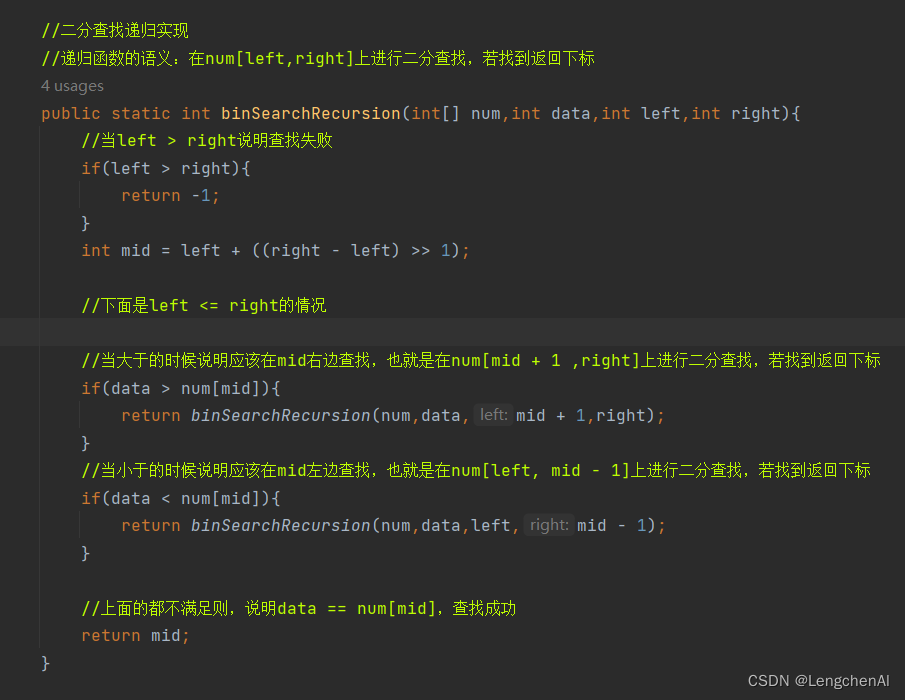
c. 注意：一个函数返回值的坑 ：在一个具有返回值的函数中必须有一个return语句不能存在于任何的结构之中(循环，分支)，如下图就会报错

 

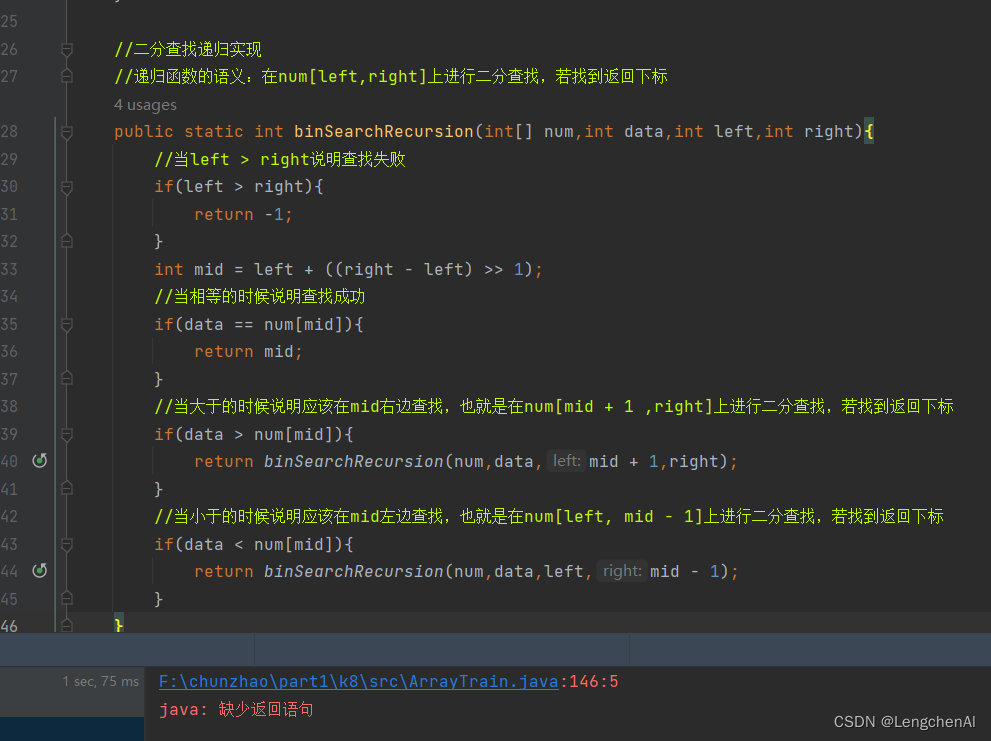
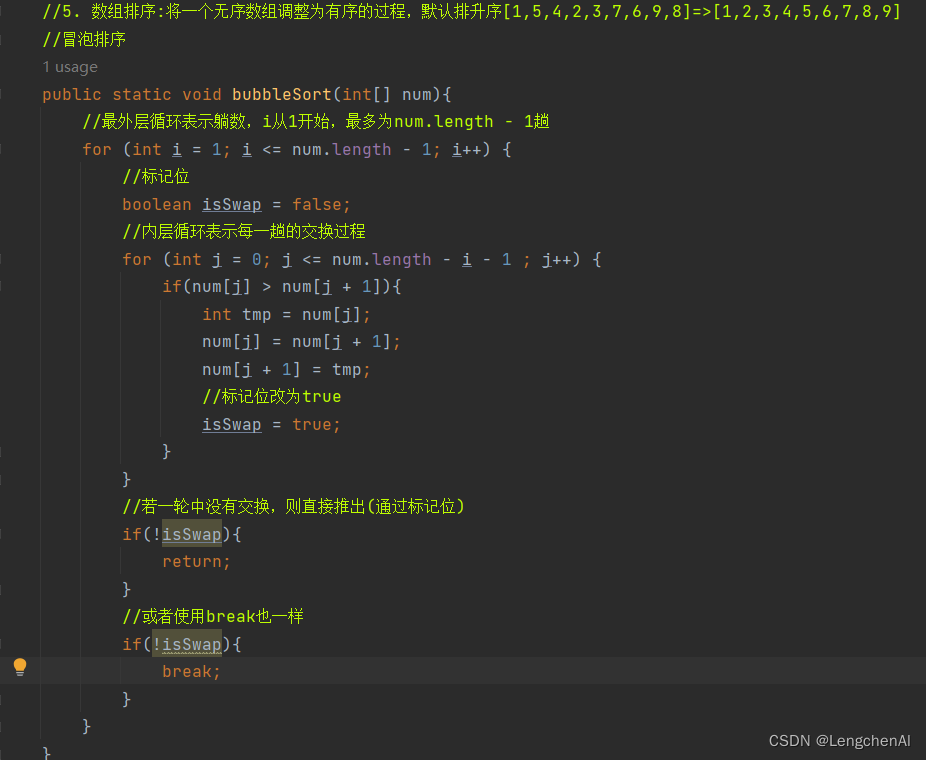
第五题：数组排序~冒泡排序

 (1)算法思想

A. 在任何一种排序算法中，都需要关注两个区间：

a. 未排序数组区间：初始为数组未排序数组区间下标为[0...n-1]

b. 已排序数组区间：初始为空 []

B. 冒泡排序规则：

a. 每一趟：left = 0,right = 1。让arr[left] > arr[right]的时候，交换两者的值，否则不交换，然后left 和 right分别+1。

b. 交换n-1趟后结束(当走完n-1趟的时候未排序数组区间只剩一个元素，天然有序)

c. 若有某一趟没有发生交换，则直接结束

C. 冒泡排序原理：每一趟都会将未排序数组中的最大值放到且排序数组区间的最末尾(例如第一趟排序：未排序数组区间：[0...n-2]; 已排序数组区间：[n-1])。最多为n趟，则排序结束。当某一轮未发生交换的时候，则说明本身有序，直接结束。

(2)代码实现