【山大909算法题】2015-T2

1.原题

编写算法，删除二叉搜索树（二叉排序树）的最小元素。叙述算法思想并给出算法实现，分析算法复杂性。二叉树采用链式存储结构，节点结构如下：（图略）其中data表示节点存储的数据，lchild和rchild分别表示指向左子节点的指针和指向右子节点的指针。

2.算法思想

1.是否为空；

2.非空且没有左孩子，说明根结点是最小的；

3.非空有左孩子，找到最左下角，再判断该结点是否有右孩子

3.关键代码

/**
 * @struct treeNode
 * @brief 二叉搜索树节点结构
 */
struct treeNode {
    int data; /**< 节点的数据 */
    struct treeNode *lchild; /**< 左子节点指针 */
    struct treeNode *rchild; /**< 右子节点指针 */
};

/**
 * @brief 删除最小节点
 *
 * 删除二叉搜索树中最小的节点。
 *
 * @param root 二叉搜索树的根节点指针
 * @return struct treeNode* 返回删除最小节点后的根节点指针
 */
struct treeNode *deleteMinNode(struct treeNode *root) {
    struct treeNode *current = root;
    if (root == NULL) {
        printf("This is an empty tree.\n");
        return NULL;
    } else if (root->lchild == NULL) { // 左子树为空，则根为最小结点，删除根，令右孩子为根
        printf("The minimum root is %d.\n", root->data);
        free(current);
        return root->rchild;
    } else {
        struct treeNode *parent;
        while (current->lchild != NULL) { // 找到最左下角的结点
            parent = current;
            current = current->lchild;
        }
        printf("The minimum root is %d.\n", current->data);

        if (current->rchild != NULL) { // 如果有右孩子，则需要把右孩子放到自己的位置上
            parent->lchild = current->rchild;
        } else { // 没有右孩子，删除该结点即可
            parent->lchild = NULL;
            free(current);
        }

        return root;
    }
}

4.完整代码

#include <stdio.h>
#include <stdlib.h>

/**
 * @struct treeNode
 * @brief 二叉搜索树节点结构
 */
struct treeNode {
    int data; /**< 节点的数据 */
    struct treeNode *lchild; /**< 左子节点指针 */
    struct treeNode *rchild; /**< 右子节点指针 */
};

/**
 * @brief 删除最小节点
 *
 * 删除二叉搜索树中最小的节点。
 *
 * @param root 二叉搜索树的根节点指针
 * @return struct treeNode* 返回删除最小节点后的根节点指针
 */
struct treeNode *deleteMinNode(struct treeNode *root) {
    struct treeNode *current = root;
    if (root == NULL) {
        printf("This is an empty tree.\n");
        return NULL;
    } else if (root->lchild == NULL) { // 左子树为空，则根为最小结点，删除根，令右孩子为根
        printf("The minimum root is %d.\n", root->data);
        free(current);
        return root->rchild;
    } else {
        struct treeNode *parent;
        while (current->lchild != NULL) { // 找到最左下角的结点
            parent = current;
            current = current->lchild;
        }
        printf("The minimum root is %d.\n", current->data);

        if (current->rchild != NULL) { // 如果有右孩子，则需要把右孩子放到自己的位置上
            parent->lchild = current->rchild;
        } else { // 没有右孩子，删除该结点即可
            parent->lchild = NULL;
            free(current);
        }

        return root;
    }
}

/**
 * @brief 创建新节点
 *
 * 创建并返回一个新的二叉搜索树节点。
 *
 * @param value 节点值
 * @return struct treeNode* 返回创建的新节点
 */
struct treeNode *createNode(int value) {
    struct treeNode *newNode = (struct treeNode *) malloc(sizeof(struct treeNode));
    newNode->data = value;
    newNode->lchild = NULL;
    newNode->rchild = NULL;
    return newNode;
}

/**
 * @brief 向二叉搜索树中插入节点
 *
 * 向二叉搜索树中插入一个节点。
 *
 * @param node 二叉搜索树的根节点指针
 * @param value 待插入的节点值
 * @return struct treeNode* 返回插入节点后的根节点指针
 */
struct treeNode *insert(struct treeNode *node, int value) {
    if (node == NULL) {
        return createNode(value);
    }

    if (value < node->data) {
        node->lchild = insert(node->lchild, value);
    } else if (value > node->data) {
        node->rchild = insert(node->rchild, value);
    }

    return node;
}

/**
 * @brief 中序遍历打印二叉搜索树节点数据
 *
 * 以中序遍历方式打印二叉搜索树节点数据。
 *
 * @param node 二叉搜索树的根节点指针
 */
void inorderTraversal(struct treeNode *node) {
    if (node != NULL) {
        inorderTraversal(node->lchild);
        printf("%d ", node->data);
        inorderTraversal(node->rchild);
    }
}

/**
 * @brief 使用括号表示法打印二叉搜索树
 *
 * 使用括号表示法打印整个二叉搜索树。
 *
 * @param node 二叉搜索树的根节点指针
 */
void printTreeInParenthesis(struct treeNode *node) {
    if (node == NULL) {
        printf("()"); // 空节点用括号表示
        return;
    }

    printf("(%d", node->data); // 输出节点的值

    // 如果节点有子节点，则进行递归打印
    if (node->lchild != NULL || node->rchild != NULL) {
        printTreeInParenthesis(node->lchild); // 递归打印左子树
        printTreeInParenthesis(node->rchild); // 递归打印右子树
    }

    printf(")"); // 节点的子树打印完毕，打印右括号
}


int main() {
    struct treeNode *root = NULL;
    int elements[] = {5, 3, 8, 2, 4, 7, 9};

    // 插入节点到二叉搜索树
    for (int i = 0; i < sizeof(elements) / sizeof(elements[0]); i++) {
        root = insert(root, elements[i]);
    }

    printf("Inorder traversal of the BST: ");
    inorderTraversal(root); // 打印中序遍历结果

    printf("\nTree in parenthesis notation: ");
    printTreeInParenthesis(root); // 使用括号表示法打印树结构

    for(int i =0;i<sizeof(elements)/ sizeof(elements[0]);i++) {
        root = deleteMinNode(root);
        printf("no.%d,Tree in parenthesis notation: ",i+1);
        printTreeInParenthesis(root); // 使用括号表示法打印树结构
    }

    return 0;
}

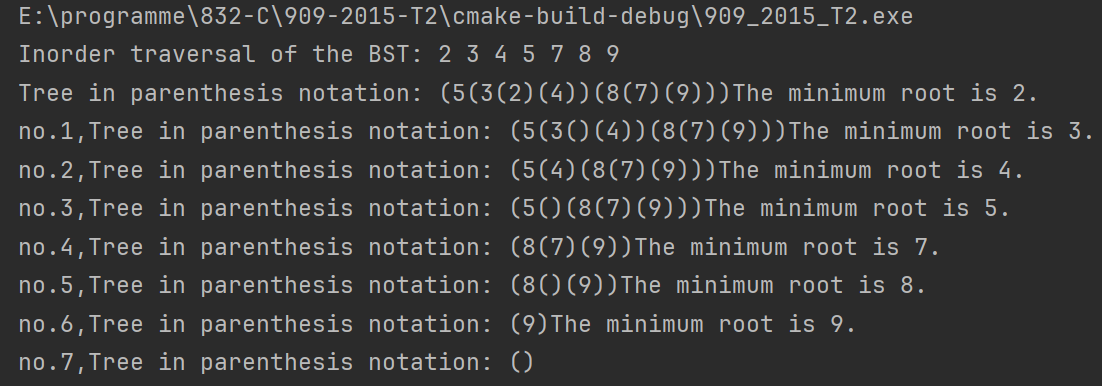
5.运行结果