C++算法刷题笔记

🔎sizeof()函数和length()函数

sizeof:

• sizeof 是一个编译时操作符，它用于获取数据类型或变量在内存中占用的字节数。
• 对于基本数据类型（例如整数、浮点数、字符等），sizeof 给出了它们在内存中的固定大小。
• 对于用户定义的复杂数据类型（例如结构体或类），sizeof 给出了整个数据结构的大小。
• 当应用于非指针数据类型时，sizeof 返回的是类型的固定大小。

length():

• length 函数通常用于字符串对象（std::string），它返回字符串中字符的数量，而不是字符串对象在内存中的大小。
• 字符串可以包含不定长度的文本数据，因此 length 函数用于获取字符串中字符的实际数量。

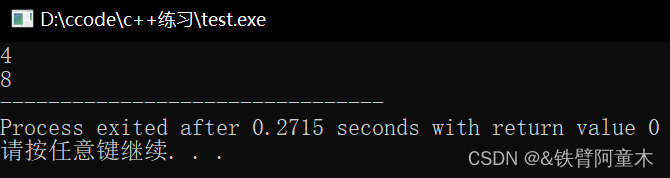
举个🌰：

#include<iostream>
using namespace std;
int main(){
	int a=90;
	string s="avhjoipu";
	cout<<sizeof(a)<<endl;
	cout<<s.length();
	return 0;
} 

🔎保留指定位数的小数

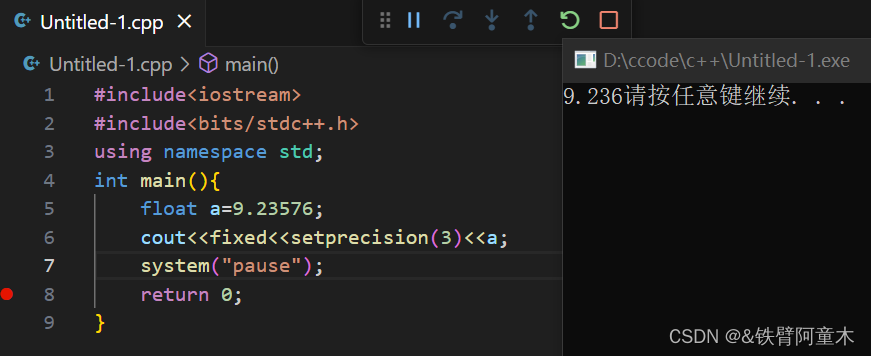
使用setprecision函数。这是一个定义在iomanip头文件中的流操作符，它可以设置输出流的精度。精度是指有效数字的位数，不一定是小数点后的位数。要保证小数点后固定的位数，还需要配合fixed流操作符使用。
举个🌰：

🔎欧拉筛

const int maxn=1e7+10;
bitset<maxn> pri;
int primes[maxn],pp=0;

int main(){
	int N=1e7,cnt=0;
	for(int i=2;i<=N;++i){
		if(!pri[i])primes[++pp]=i;
		for(int j=1;primes[j]*i<=N;++j){
			pri[primes[j]*i]=1;
			if(i%primes[j]==0)break;
		}
	}
}

🔎 c++中对数log的用法

• exp()函数：exp(n)的结果为e^n，exp 函数的输出类型是 double，它返回一个 double 类型的浮点数。

#include <iostream>
#include <cmath>
int main() {
    double x = 2.0;
    double result = exp(x); // 计算e的x次方
    std::cout << "exp(2.0) = " << result << std::endl;
    return 0;  //输出结果 exp(2.0) = 7.38906
}

• log()：是以e为底的函数，log(n)表示e的多少次方为n，输出类型也是double。
• log10()：是以10为底的函数，log10(n)表示10的多少次方为n。
• c++中使用e：自然对数e可以使用 头文件中的常数 M_E 来表示。

#include <iostream>
#include <cmath>
int main() {
    double e = M_E; // 获取自然对数e的值
    std::cout << "The value of e is: " << e << std::endl;
    return 0;
}

• 自定义m为底：log(n)/log(m)

🔎 bitset

在欧拉筛中用到的一个容器bitset，是一个(比特)二进制(0和1)的集合，在初始化定义时默认全为零，但是在使用的时候发现一个问题bitset<size> namedbyou中size必须是常量。

🔎round()函数

• 是什么？
  round函数用于对float、double以及longdouble四舍五入到最接近的整数。
• 如何使用？
  语法格式如下：

#include <math.h> //需要包含头文件

extern float roundf(float);//参数为flot类型
extern double round(double);//参数为double类型
extern long double roundl(long double);//参数为long double类型

📍round函数返回的是double类型，永远都是！下面是输出类型测试，顺便学习一下typeinfo这个头文件的使用。

#include <iostream>
#include<typeinfo>
#include<math.h>
using namespace std;
int main()
{
	float a=3.2345;
	double b=8.67868658;
	cout<<round(a)<<endl;
	cout<<typeid(round(a)).name()<<endl;
	cout<<round(b)<<endl;
	cout<<typeid(round(b)).name()<<endl;
  return 0;
}

输出结果：

3
d
9
d

🔎memset VS. for循环为数组赋值

🌰：为数组中的每个元素赋初始值2021
方式一

int a[10];
memset(a,2021,sizeof(a));

方式二

int a[10];
for(int i=0;i<10;i++){
a[i]=2021;

• memset 函数是用来初始化内存块的，第二个参数是一个整数值，它会被强制转换为一个字节，然后用于填充整个内存块。所以，memset(a, 2021, sizeof(a)) 会将数组 a 中的每个字节都设置为 2021（在不同机器上可能会有不同的结果，因为 2021 被转换为一个字节，高位字节会被截断）。
• 而通过循环为数组 a 的每个值赋值为 2021，会确保每个元素都被设置为 2021，而不仅仅是每个字节。这是更常见的方式来初始化整数数组，因为它会将整数值分别赋给每个数组元素，而不会导致字节截断问题。

🔎c++类型转换中的 +‘0’ 与 -‘0’

此前一直没有注意到’0‘前面+与-的差异：
char转int: char类型的数-’0‘
int转char: int类型的数+’0‘
此处做一些常用类型转换的补充：
int转string: stringType_num=to_string(intType_num)//头文件#include<string>
string转int: intType_num=stoi(TringType_num)//头文件#include<string>

🔎以“变量”字符初始化数组大小

const int N=1e7;
int dp[N];

• why通过使用const来定义N，在后续调用dp时才不会报错?
  使用const来定义N有助于确保N在编译时被视为一个常量。这意味着N的值在编译时就被确定，并且在程序执行期间不可修改。对于数组大小的定义，大多数编译器要求使用常量来确定数组的大小。使用const关键字定义的常量在编译时会被直接替换为其值

🔎 取整、四舍五入

四舍五入：round()函数
向上取整：ceil()函数
向下取整：floor()函数

注意头文件#include<cmath>

🔎 最大最小值设定

INT_MIN:-2147483648
INT_MAX:2147483647
LONG_MIN:-2147483648
LONG_MAX:2147483647
LLONG_MIN:-9223372036854775808
LLONG_MAX:9223372036854775807	

🔎整型数字0~9–>00~09

在C++中，可以使用setw()函数来设置输出流对象的宽度。然后再结合left或者right修饰符来控制输出时的对齐方式。（默认右对齐）

#include <iostream>
#include <iomanip> // 包含 setw() 所需要的头文件
using namespace std;
 
int main() {
    int num = 5;
    
    cout << "原始值为：" << num << endl;
    cout << "按两位数输出并左对齐：";
    cout << left << setfill('0') << setw(2) << num << endl;
    cout << "按两位数输出并右对齐：";
    cout << right << setfill('0') << setw(2) << num << endl;
    
    return 0;
}

输出结果

原始值为：5
按两位数输出并左对齐：05
按两位数输出并右对齐：  5

🔎lowbit()运算

非负整数n在二进制表示下最低位1及其后面的0构成的数值。

e.g. lowbit(44)=lowbit((101100)2)=(100)2=4			

~n+1=-n(~ 表示取反)
lowbit(n)=n&(~n+1)=n&-n								

lowbit的用途？
我们可以利用它来实现一些高效的算法，比如求一个数的二进制表示中有多少个1，或者维护一个数组的前缀和，快速求树状数组的层数 等等

lowbit 也可以快速求出这个二进制数的末尾有几个0, lowbit(x) = 2^{k} ,k 则表示末尾有几个零

🔎while(scanf(“…”)==…)

刷题时遇到
while (scanf("%d-%d-%d %d:%d:%d", &y, &mo, &d, &h, &mi, &s) == 6)
最初不理解为什么要判断等于6，查阅发现循环的条件是scanf函数的返回值。scanf在成功读取数据后会返回成功匹配的输入项数量。在这个例子中，如果用户输入了6个数据项（年、月、日、时、分、秒），scanf会返回6，循环会继续执行；如果用户输入的数据项数量不是6，或者输入的格式不正确（例如，输入了字母或特殊字符），scanf会返回一个小于6的值，循环会终止。

🔎getline函数

getline是C++标准库函数；它有两种形式，一种是头文件< istream >中输入流成员函数；一种在头文件< string >中普通函数；

它遇到以下情况发生会导致生成的本字符串结束：
(1)到文件结束，(2)遇到函数的定界符，(3)输入达到最大限度。
下面的代码将getline用于字符串分割。

#include <iostream>
#include <string>
#include <vector>
#include <sstream>

int main() {
    std::string a = "01.02.033.32";
    std::vector<int> intArray;

    // 使用stringstream来移除分隔符并转换为整数
    std::stringstream ss(a);
    std::string token;
    while (getline(ss, token, '.')) {
        int num = std::stoi(token);
        intArray.push_back(num);
    }

    // 输出转换后的整数数组
    for (int num : intArray) {
        std::cout << num << " ";
    }
    std::cout << std::endl;

    return 0;
}

🌰：输入的字符串里包含空格，如何以空格分割存储相应的字符串

#include <iostream>
#include <vector>
#include <sstream>
#include <string>

int main() {
    std::vector<std::string> res;
    std::string str;
    std::string line;

    // 读取一整行输入
    std::getline(std::cin, line);

    // 使用istringstream来分割字符串
    std::istringstream iss(line);
    while (std::getline(iss, str, ' ')) {
        res.push_back(str);
    }

    // 输出结果以验证
    for (const auto& s : res) {
        std::cout << s << std::endl;
    }

    return 0;
}

📍：在 C++ 标准库中，std::getline 函数有两个重载版本。第一个版本用于从 std::istream 类（如 std::cin）读取一行，直到遇到换行符（\n）或结束文件（EOF），并自动丢弃换行符。这个版本的 std::getline 没有第三个参数。

第二个版本是模板函数，它允许从任何输入流中读取，直到遇到指定的分隔符。这个版本有三个参数：输入流、用于存储读取内容的字符串变量，以及分隔符。这个版本的 std::getline 可以读取到指定的分隔符为止，但不包括分隔符本身。

🔎数组初始化遇到的问题

问题

int N=2e5+10;
int a[N];
int main(){
...
...
}

通过这种方式声明数组，代码在运行时报错
[Error] array bound is not an integer constant before ']' token main内部调用了a的地方：[Error] 'a' was not declared in this scope
解决办法

const int N=2e5+10;
int a[N];
int main(){
...
...
}

在C++中，当声明一个数组并立即初始化它时，数组的大小必须是一个编译时常量（即在编译时就能确定的值）。这是因为编译器需要知道分配多少内存来存储数组。如果数组的大小是一个运行时才能确定的值，编译器就无法在编译时为数组分配正确的内存空间。
例如：

int N; // 未初始化的变量，其值在运行时确定
int a[N]; // 错误：N不是编译时常量

或者：

int N = 2e5 + 10; // 在main函数之前声明，但未使用const
int a[N]; // 错误：N不是编译时常量

在这两种情况下，N 的值都是在运行时确定的，因此编译器无法在编译时知道数组 a 需要多少内存。为了解决这个问题，你需要确保数组的大小是一个编译时常量，或者在运行时动态地分配数组。

• const 关键字用于声明一个常量对象，它的值在初始化后就不能被修改。const 对象的值可以在运行时确定，也可以在编译时确定。(需要在编译时执行计算或者需要更严格的常量表达式时，应该使用 constexpr)

const int max_value = 100; // 编译时确定
const int value = 2 * 3; // 编译时确定
const int result = calculate(); // 运行时确定

🔎dfs模板

void dfs(int step){
	if(达到目的){
		输出解
		返回
	}
	合理的剪枝操作
	for(int i=1;i<=枚举数;i++){
		if(满足条件){
			更新状态位;
			dfs(step+1);
			恢复状态位;
		}
	}
}

🔎全排列问题由1~n组成的所有不重复的数字序列

方法1 dfs

using namespace std;
int n,a[10],flag[10]={0};
void dfs(int step){
	if(step==n){
		for(int i=0;i<n;i++){
			cout<<a[i];
		}
		return;
	}
	for(int i=1;i<n;i++){
		if(flag[i]==0){
			a[step]=i;
			flag[i]=1;
			dfs(step+1);
			flag[i]=0;
		}
	}
} 

方法2 next_permutation
next_permutation函数作用：求当前排列的下一排列
头文件：algorithm
返回值：true/false
使用方法：和sort的参数一样，一般传两个参数，第一个是排列开始的地址，第二个是排列结束的下一个地址，如实现数组第1-3排列的下一个排列:next_permutation(a,a+3)。一般作用对象是数组。
note： 根据net_permutaion的原理可知，当排序的对象为降序时默认已经排列好，所以在解题时如果想得到给定对象的全排列需要先对排列对象进行升序排列的初始化操作。👇

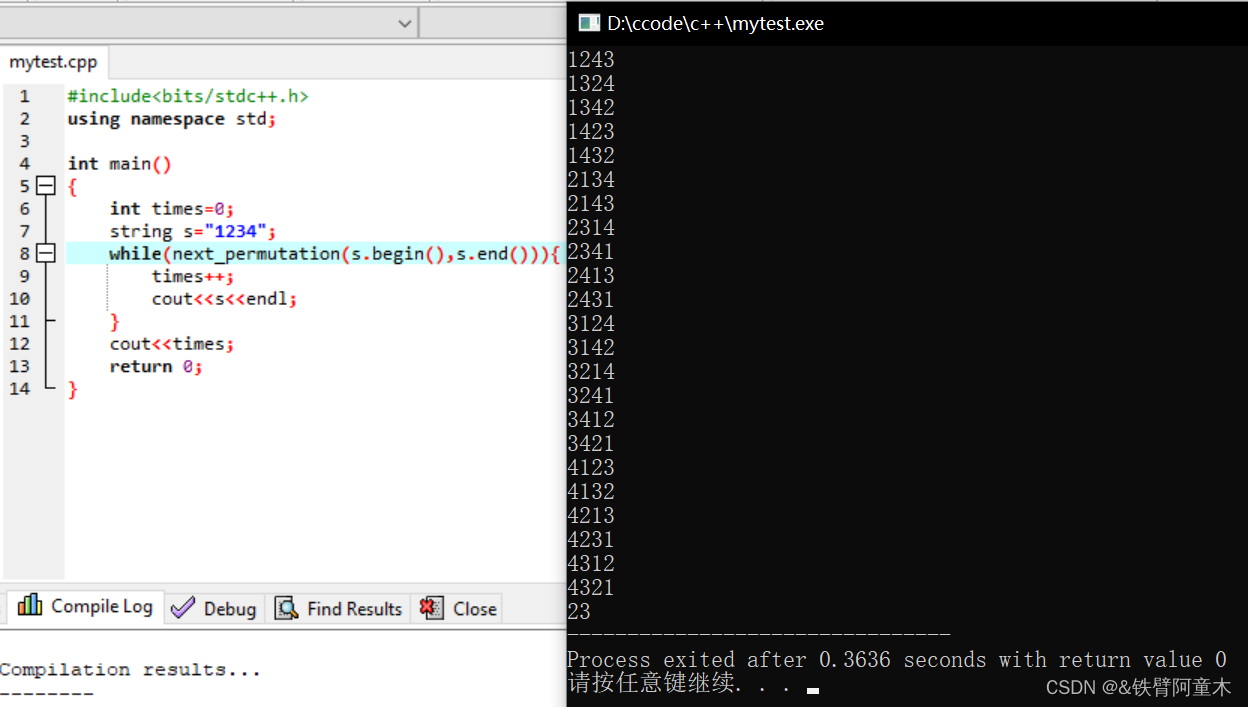
vs.

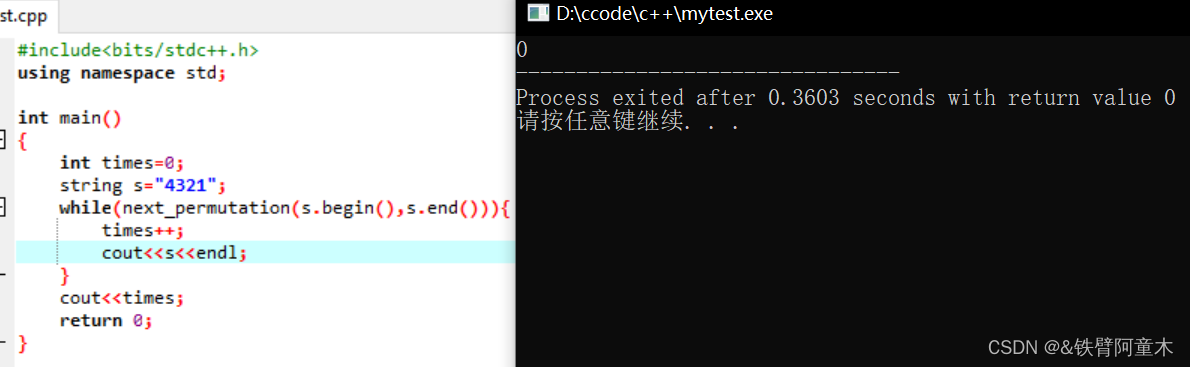
🔎 利用欧几里得算法求最小公倍数

欧几里得算法是用来求最大公约数的高效算法，在这里可以用来求小公倍数

eg: 通过键盘输入3个int类型数据，求他们的最小公倍数

#include <iostream>
#include<bits/stdc++.h>
using namespace std;
int gcb(int a,int b){
  return b==0?a:gcb(b,a%b);
}
int main()
{
  // 请在此输入您的代码
  int a[3]={0};
  for(int i=0;i<3;i++){
    cin>>a[i];
  }
  sort(a,a+3);
  int res=a[0];
  for(int i=1;i<3;i++){
    res=(res*a[i])/gcb(res,a[i]);
  }
  cout<<res;

  return 0;
}

🔎修改变量名称long long–>ll

有两种方法：

1. 在main之前添加

typedef long long ll;

2. 在main之前添加

#define ll long long

🔎switch语句结构

太长时间没用了，编译的时候居然在这里报错了，上网查阅发现switch后面的括号不能漏掉！

switch(条件表达式)
{
	case 结果1: 语句1; break;
	case 结果2: 语句2; break;
		...
	case 结果3: 语句3; break;
	default: 语句n+1; break;
}

🔎运算优先级

state >> i + 1这句代码的意思是将state右移i+1位，而不是state右移i位后再加一！
之所以理解错误是混淆了c++中运算符的优先级：
四则运算>位运算>逻辑运算
四则运算符：+、-、*、/、%
位运算符：&、| 、^ 、~ 、<< 、>>
逻辑运算符：&&、||、！

🔎对自定义结构体内容按需排序

copy from 蓝桥杯中 “外卖优先级”中的作答

struct node{
 int ts;
 int id;
};
node a[100002];
bool cmp(node x,node y){
 if(x.id!=y.id){
   return x.id<y.id;
 }
 else{
   return x.ts<y.ts;
 }
}

🔎判断二进制表示的数是否存在"相邻"1？

纵向
首先想到的方法是 同步右移+判断最后一位是否都为1
然而通过两道题的题解发现他们都使用了&运算来判断：
eg:a=0101011,b=1001111
if(a&b)那么必定存在上下相邻位置a、b中对应的数字皆为1
if((a&b)==0)那么a、b中一定不会出现相同的位上皆为1的情况
横向
eg:a=100101 判断a中是否存在相邻位置都为1的情况
首先想到的是利用 while循环+右移 逐个判断
实则一步右移就能判断出来：if((a&(a>>1))==0)那么a中一定没有相邻的1，反之一定有相邻的1.

🔎结构体的使用

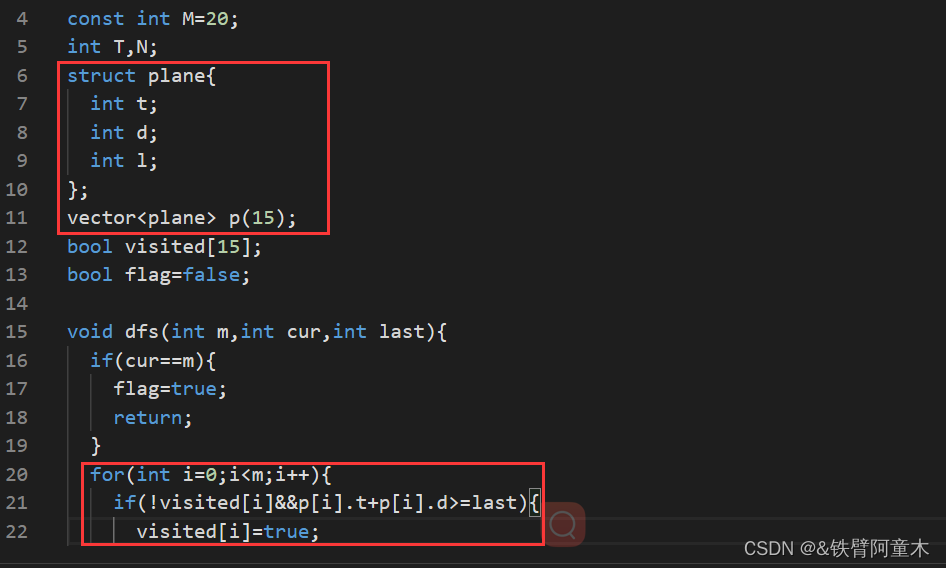
🔎大小写字母转换

四种方式

🔎数组初始化

在未手动给数组赋初始值的前提下，系统会自动为其赋值得，数组定义在main函数之前或之后，系统赋的值是有差别的！！

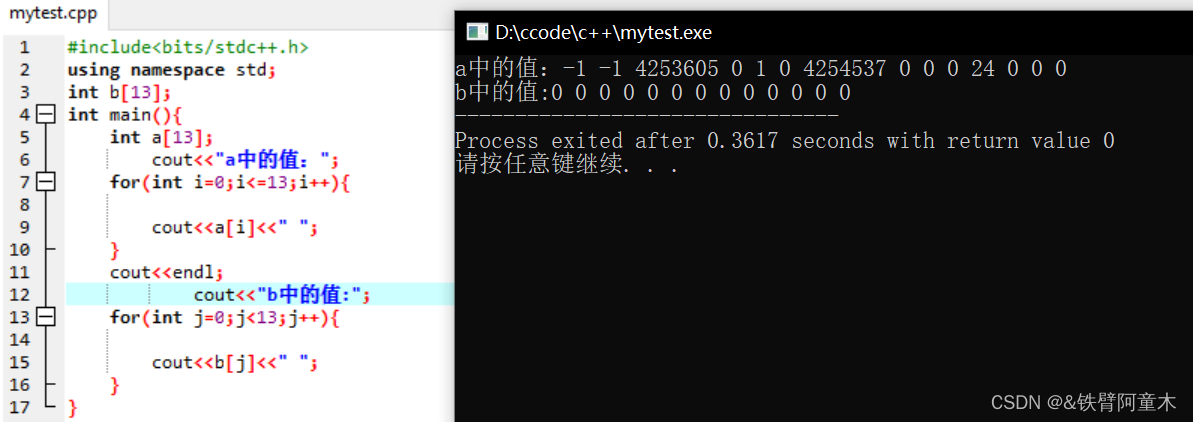
所以，想要自动为数组赋值全0时，一定要把数组定义在main函数外面！

🔎异或的使用

“可截取性”： b⊕c⊕d=(a⊕b⊕c⊕d)⊕a
主要还是因为异或运算是满足结合律和交换律的：
(a⊕b⊕c⊕d)⊕a=a⊕a⊕b⊕c⊕d=(a⊕a)⊕b⊕c⊕d=0⊕b⊕c⊕d=b⊕c⊕d

📌为什么可以做这一部化简？

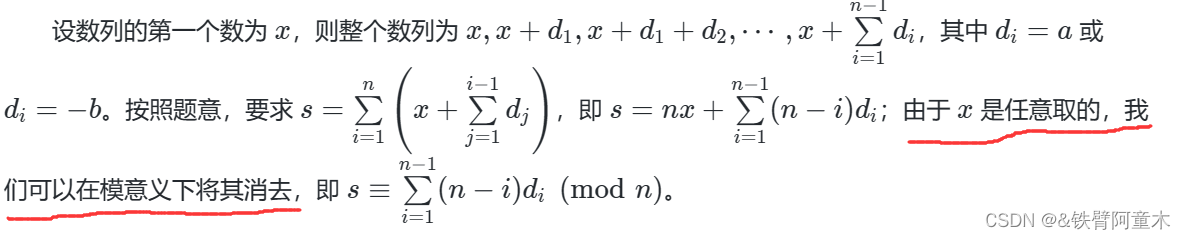
类中成员变量初始化问题

正确代码：

class Trie {
private:
    bool isEnd;
    Trie* next[26];
public:
    Trie() {
        isEnd = false;
        memset(next, 0, sizeof(next));
    }
    
    void insert(string word) {
        Trie* node = this;
        for (char c : word) {
            if (node->next[c-'a'] == NULL) {
                node->next[c-'a'] = new Trie();
            }
            node = node->next[c-'a'];
        }
        node->isEnd = true;
    }
    
    bool search(string word) {
        Trie* node = this;
        for (char c : word) {
            node = node->next[c - 'a'];
            if (node == NULL) {
                return false;
            }
        }
        return node->isEnd;
    }
    
    bool startsWith(string prefix) {
        Trie* node = this;
        for (char c : prefix) {
            node = node->next[c-'a'];
            if (node == NULL) {
                return false;
            }
        }
        return true;
    }
};


作者：路漫漫我不畏
链接：https://leetcode.cn/problems/implement-trie-prefix-tree/solutions/98390/trie-tree-de-shi-xian-gua-he-chu-xue-zhe-by-huwt/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

我写的代码：

class Trie {
private:

public:
    Trie() {
        bool isEnd;
        Trie* next[26];

    }
    
    void insert(string word) {
        Trie* node=this;
        for(int i=0;word[i];i++){
            if(node->next[word-'a']==NULL){
                node->next[word-'a']=new Trie;
            }
            node=node->next[word[i]-'a'];
        }
        node->isEnd=true;
    }
    
    bool search(string word) {
        Trie* node=this;
        for(char c:word){
            if(node->next[c-'a']==NULL){
                return false;
            }
            node=node->next[c-'a'];
        }
        return node->isEnd;
    }

    
    bool startsWith(string prefix) {
        Trie* node=this;
        for(char c:word){
            node=node->next[c-'a'];
            if(node==NULL){
                return false;
            }  
        }
    }
};

运行结果：编译出错 Line 12: Char 22: error: no member named 'next' in 'Trie' 12 | if(node->next[word-'a']==NULL){ | ~~~~ ^
原因：如果去掉private关键字，并且将构造函数Trie()中的初始化代码改为：

Trie() {
    bool isEnd;
    Trie* next[26];
}

这将导致几个问题：

作用域问题：在构造函数中声明的局部变量isEnd和next数组只会在构造函数的作用域内有效。这意味着它们不会成为类的成员变量，因此无法在类的其他成员函数中使用。

内存分配问题：如果next数组不是作为成员变量存在，那么它将在构造函数结束后被销毁，导致所有指向这个数组的指针都变成悬挂指针（dangling pointer），这将引发未定义行为。

数据持久性问题：由于isEnd和next数组不是类的成员变量，它们不会在对象的生命周期内持续存在，这使得Trie节点无法正常工作。

内存泄漏问题：如果next数组中的元素被动态分配了（如new Trie()），而它们不是类的成员变量，那么这些动态分配的内存将无法被正确释放，导致内存泄漏。

代码逻辑错误：即使不考虑上述问题，构造函数中的这种声明方式也会导致逻辑错误，因为isEnd和next数组在构造函数结束后就不再存在，这与Trie节点的预期功能相矛盾。

总之，去掉private关键字并错误地声明构造函数会导致代码逻辑错误和潜在的内存问题，使得Trie类无法正常工作。正确的做法是保持isEnd和next数组作为类的私有成员变量，并在构造函数中正确初始化它们。

🔎记录一下关于vector的踩坑

由于在初始化vector类型变量时未初始化大小，导致后面在使用[ ]和push_back赋值时没反应，进而组织了后面代码的执行，也是很奇怪，我的错误操作是在for循环里面的，循环外面的cout语句为什么没办法正常执行呢？总之，这一个bug让我花了很多时间，不过最后那道题目依然没有成功运行，时间复杂度太高了…无论遇到什么题目貌似总是习惯通过暴力求解（还要加上冗长的debug时间），偶尔运气比较好可以搞出来，大部分时候时间复杂度是不过关的，这个时候已经被debug耗尽了所有力气，一点优化的思路都没有…

🔎24小时制转换为秒

 int timeToSeconds(const string& timeStr) {
 int h, m, s; char c; 
istringstream ss(timeStr);
 ss >> h >> c >> m >> c >> s;
 return h * 3600 + m * 60 + s;
 }

📍: 关于其第四行代码解读：这个过程会按照时间字符串的格式（小时、冒号、分钟、冒号、秒）依次读取。
第一个 >> 将小时部分读入 h。
第二个 >> 将小时和分钟之间的冒号读入 c。
第三个 >> 将分钟部分读入 m。
第四个 >> 将分钟和秒之间的冒号读入 c。
第五个 >> 将秒部分读入 s。

🔎秒转换为24小时制

 string secondsToTime(int totalSeconds) {
    int h, m, s;
    h = totalSeconds / 3600; // 计算小时数
    m = (totalSeconds % 3600) / 60; // 计算分钟数
    s = totalSeconds % 60; // 计算秒数

    // 使用ostringstream来构建格式化的字符串
    ostringstream oss;
    oss << setfill('0') << setw(2) << h << ":"
        << setfill('0') << setw(2) << m << ":"
        << setfill('0') << setw(2) << s;
    
    return oss.str();
}

📍构建格式化字符串部分代码解读：

• ostringstream oss：这行代码创建了一个ostringstream对象，名为oss。
• oss << setfill(‘0’) << setw(2) << h：oss << 是将数据插入到oss对象中的方式。setfill(‘0’) 设置填充字符为’0’，这意味着如果后续的字段宽度不够，将用’0’来填充。setw(2) 设置字段宽度为2。这意味着接下来的插入操作将至少占用2个字符的宽度。h 是要插入的第一个数据，即小时数。
• oss.str() 是获取ostringstream对象中构建的字符串的方法。

🔎排序结构体

为具有多属性的对象依据各属性优先级进行排序时，往往相到自定义结构体，重写cmp函数的方法。下面为采用qsort和sort两种比较函数时，代码上的一些差异。
下面的代码编写基于如下问题：

1、使用qsort函数

#include <iostream>
#include<bits/stdc++.h>
using namespace std;
int N;
typedef struct gdp{
	string name;
	int first;
	int second;
	int third;
	int total;
} GDP; 
int cmp(const void* a,const void* b){
	const GDP* gdpA = (const GDP*)a;
    const GDP* gdpB = (const GDP*)b;
    return (gdpB->total - gdpA->total);
}
int main()
{
  cin>>N;
  GDP city[N];
  for(int i=0;i<N;i++){
  	cin>>city[i].name>>city[i].first>>city[i].second>>city[i].third;
  	city[i].total=city[i].first+city[i].second+city[i].third;
  }
  qsort(city,N,sizeof(city[0]),cmp);
  cout<<city[0].name;
  return 0;
}

📍：使用qsort函数排序时，cmp函数在编写时要注意参数类型一定是const void*，难点是在面对不同数据类型的比较对象时，要做相应的类型转换！
qsort详尽用法

2、使用sort函数

#include <iostream>
#include <algorithm> // 使用std::sort而不是qsort
#include <vector>
using namespace std;

typedef struct gdp {
    string name;
    int first;
    int second;
    int third;
    int total;
} GDP;

// 比较函数，用于std::sort
bool cmp(const GDP& a, const GDP& b) {
    return a.total > b.total; // 降序排序
}

int main() {
    int N;
    cin >> N;
    vector<GDP> city(N);
    for (int i = 0; i < N; i++) {
        cin >> city[i].name >> city[i].first >> city[i].second >> city[i].third;
        city[i].total = city[i].first + city[i].second + city[i].third;
    }
    
    // 使用std::sort和cmp函数对city数组进行排序
    sort(city.begin(), city.end(), cmp);
    
    cout << city[0].name << endl;
    
    return 0;
}

📍：将cmp函数的参数改为const GDP&类型；修改了cmp函数的返回类型为bool，这是std::sort所期望的；使用vector而不是固定大小的数组，这样代码更加灵活和安全。
sort在结构体排序中的使用

🔎vector中erase的使用

在 C++ 标准库中，std::vector 提供了 erase 函数，用于移除向量中的一个或多个元素。erase 函数接受一个或两个迭代器参数，指定要移除的元素范围，并返回指向被移除元素之后元素的迭代器。

• 移除单个元素

std::vector<int> vec = {1, 2, 3, 4, 5};
vec.erase(vec.begin() + 1); // 移除第二个元素（值为 2）
// vec 现在是 {1, 3, 4, 5}

• 移除元素范围

std::vector<int> vec = {1, 2, 3, 4, 5};
vec.erase(vec.begin() + 1, vec.begin() + 3); // 移除从第二个元素到第三个元素（包括第二个，不包括第三个）
// vec 现在是 {1, 4, 5}

🔎利用c_str()函数来自定义起始位置的获取字符串

🔎利用isapha函数判断一个字符是否是英文字母（不区分小写）

#include<iostream>
#include <cctype> // 包含字符处理函数

int main() {
    char ch;
    std::cout << "Enter a character: ";
    std::cin >> ch;

    if (isalpha(ch)) {
        std::cout << ch << " is an alphabet letter." << std::endl;
    } else {
        std::cout << ch << " is not an alphabet letter." << std::endl;
    }

    return 0;
}

🔎差分数组

从入门到精通-差分数组
差分数组和前缀和数组通常是配合使用的，差分数组负责对数组区间高效更新，前缀和数组负责对数组区间快速查询。

🔎最小生成树prim算法模板

struct edge{int v,w;}
vector<edge> e[N];
int d[N], vis[N]
bool prime(int s){
	for(int i=0;i<=n;i++)d[i]=inf;
	d[s]=0;
	for(int i=1;i<=n;i++){
		int u=0;
		for(int j=1;j<=n;j++){
			if(!vis[j]&&d[j]<d[u])u=j;
		}
		vis[u]=1;
		ans+=d[u];
		if(d[u]!=inf)cnt++;
		for(auto ed:e[u]){
			int v=ed.v,w=ed.w;
			if(d[v]>w)d[v]=w;
		}
	}
	return cnt==n;
}

🔎最小生成树Kruskal算法

struct edge{
int u,v,w;
bool operator<(const edge &t)const
{return w<t.w;}
}e[N];
int fa[N],ans,cnt;

int find(int x){
	if(fa[x]==x)return x;
	return fa[x]=find(fa[x]);
}
bool kruskal(){
	sort(e,e+m);//重写了<，所以这里sort知道是根据w来排序
	for(int i=1;i<=n;i++)fa[i]=i;
	for(int i=0;i<m;i++){
		int x=find(e[i].u);
		int y=find(e[i].v);
		if(x!=y){
			fa[x]=y;
			ans+=e[i].w;
			cnt++;
		}
	}
	return cnt==n-1;
}

🔎最长公共子串

dp[i][j]: 以a[i]和b[j]为结尾的公共子串的长度。

for(int i=1;i<=strlen(a);i++){
	for(int j=1;j<=strlen(b);j++){
		if(a[i-1]==b[j-1])//注意下标
			dp[i][j]=dp[i-1][j-1]+1;
		else
			dp[i][j]=0;
		if(dp[i][j]>max)
			max=dp[i][j];
	}
}
cout<<max;

🔎priority_queue的用法

优先队列的使用方法

🔎关于自定义排序

👉在sort函数中

struct edge{
  int u,v,w;
}e[M];

bool cmp(edge a,edge b){
  return a.w<b.w;
}
  sort(e,e+m,cmp);

数组 e 中的前 m 个元素将按照 w 的值从小到大排序，即升序排序。

👉在priority_queue类型数据中

struct cmp {
    bool operator()(const pair<int,ll>& a, const pair<int,ll>& b) {
        return a.second > b.second;
    }
}; 
priority_queue<pair<int,ll>, vector<pair<int,ll>>, cmp> q;

队列中的元素会按照 second 值从小到大排序，即升序排序。

Q1： 为什么同样是升序排序，一个return <，一个return >?
Q2： 对于priority_queue自定义排序，能否直接定义bool cmp函数?

🎯A1:

• return a.w < b.w; 是升序。sort 默认会根据比较函数的结果决定元素的排列顺序。如果 cmp(a, b) 返回 true，表示 a 应该排在 b 前面。因此，return a.w < b.w; 表示：如果 a.w 小于 b.w，a 应该排在 b 前面。最终结果是：数组按照 w 的值从小到大排序（升序）。
• return a.second > b.second; 是小顶堆。priority_queue 默认是一个大顶堆（堆顶元素是最大的）。自定义比较器的作用是改变堆的排序规则：
  如果 cmp(a, b) 返回 true，表示 a 的优先级比 b 低（即 a 应该排在 b 后面）。因此，return a.second > b.second; 表示：如果 a.second 大于 b.second，表明a 的优先级更低，应该排在 b 后面。最终结果是：优先队列按照 second 的值从小到大排序（小顶堆）。
  📍可以理解为cmp改变的是对优先级的定义，priority_queue依然是根据优先级从高到底排序的。

🎯A2: 不可以。priority_queue 的比较器需要是一个仿函数（functor）或者一个函数对象，而不是普通的函数。如果直接将普通函数 cmp 传递给 priority_queue，编译器会报错。

🔎并查集模板

int fa[N];
int find(int x){
	if(fa[x]==x) return x;
	return fa[x]=find(fa[x]);
}

void unionset(int x,int y){
	fa[find[x]]=find(y);
}

🔎最短路dijstra算法

适用于稠密图

struct edge{
  int v,w;
};
vector<edge> e[N];

void dijstra(int src){
  for(int i=0;i<=n;i++)d[i]=INT_MAX;
  d[src]=0;
  for(int i=1;i<n;i++){
    int u=0;
    for(int j=1;j<=n;j++){
      if(!vis[j]&&d[u]>d[j])u=j;
    }
    vis[u]=1;
    for(auto ed : e[u]){
      int v=ed.v;
      int w=ed.w;
      if(d[v]>d[u]+w)d[v]=d[u]+w;
    }
  }
}

适用于稀疏图（使用优先队列）

#include<bits/stdc++.h>
using namespace std;

const int ss = 0x3f3f3f3f;  // 定义"无穷大"常量（0x3f3f3f3f十进制为1061109567，满足32位int且加法不溢出）
using pii = pair<int, int>; // 定义类型别名，存储结构为（目标节点，边权值）

// Dijkstra算法实现（优先队列优化版）
// 参数：road-邻接表存储的图结构，distance-最短距离结果数组
void dijstra(vector<vector<pii>>& road, vector<int>& distance) {
    // 小顶堆优先队列，元素格式（当前距离，节点编号），按距离升序排列
    priority_queue<pii, vector<pii>, greater<pii>> qq;
    
    distance[1] = 0;       // 初始化起点（节点1）到自身的距离为0
    qq.push({0, 1});       // 起点入队，格式（距离0，节点1）

    while (!qq.empty()) {
        // 取出堆顶元素（当前已知的最短路径）
        int u = qq.top().second;       // 当前节点编号
        int now_length = qq.top().first; // 队列中记录的暂存距离
        qq.pop();

        /* 关键优化：过滤过时数据
           如果队列中记录的距离 > 最新计算的距离，说明该节点已被更优路径更新
           此记录已失效，跳过后续处理 */
        if (now_length != distance[u]) continue;

        // 遍历当前节点的所有邻接边
        for (auto& edge : road[u]) {
            int v = edge.first;   // 相邻节点编号
            int w = edge.second;  // u到v的边权值

            /* 松弛操作：尝试通过u优化v的路径
               distance[u] + w 表示通过u到达v的新距离
               如果新距离比已知更短，更新并加入队列 */
            if (distance[u] + w < distance[v]) {
                distance[v] = distance[u] + w;  // 发现更短路径，更新v的最短距离
                qq.push({distance[v], v});      // 新距离入队（允许重复节点）
            }
        }
    }
}

int main() {
    int n, m;            // n-节点总数，m-边总数
    cin >> n >> m;

    // 初始化邻接表（节点编号1~n，road[0]未使用）
    vector<vector<pii>> road(n + 1);
    // 初始化距离数组：所有节点初始距离为无穷大
    vector<int> distance(n + 1, ss);  

    // 构建图的邻接表
    for (int i = 0; i < m; i++) {
        int a, b, c;
        cin >> a >> b >> c;          // 读取有向边：起点a，终点b，边权c
        road[a].push_back(make_pair(b,c));
    }

    dijstra(road, distance);  // 执行Dijkstra算法计算最短路径

    // 输出结果：若终点n不可达输出-1，否则输出最短距离
    cout << (distance[n] == ss ? -1 : distance[n]) << endl;
    return 0;
}