【深度学习-基础知识】批量归一化 (BN, Batch Normalization)

1. 背景问题

内部协变量偏移（internal covariate shift）问题：内部协变量偏移指的是在深度神经网络训练过程中，由于网络参数的更新，每一层的输入分布会发生变化，这种变化会影响到下一层的学习效果，使得训练过程变得不稳定，需要使用较小的学习率和精心设计的参数初始化策略来减轻其负面影响。

2. 实现步骤

这里以训练阶段为例进行说明：

1. 计算小批次统计量

对于每个神经网络层的输入（或激活值），首先需要计算当前小批次（mini-batch）内所有样本对应特征的均值和方差。设输入为 $X$，则均值 ${\mu }_B$ 和方差 ${\sigma }_B^2$ 分别为：
$${\mu }_B=\frac{1}{m}\sum _{i=1}^m{x}^{(i)}$$
$${\sigma }_B^2=\frac{1}{m}\sum _{i=1}^m(x^{(i)}-{\mu }_B{)}^2$$
其中，$m$ 是小批次大小，$x^{(i)}$ 表示第 $i$ 个样本的特征值。

2. 归一化处理

基于上述计算得到的均值和方差对输入数据进行归一化处理，使其均值为0，方差为1。公式如下：
$${\hat{x}}^{(i)}=\frac{x^{(i)}-{\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}}$$
其中，$ϵ$ 是一个非常小的常数（如 $10^{-8}$），用于保证数值稳定性，避免除以零的情况发生。

3. 尺度变换和偏移

为了增加模型的表达能力，允许对归一化后的输出进行线性变换，即引入两个可学习参数 $\gamma$（缩放因子）和 $\beta$（偏移因子）。变换公式如下：
$$y^{(i)}=\gamma {\hat{x}}^{(i)}+\beta$$
这里的 $y^{(i)}$ 就是经过批量归一化后的新输入，它将作为下一层的输入或者是当前层的最终输出（如果这是网络的最后一层的话）。

3. 注意点

3.1. 训练阶段和推理阶段的均值方差区别

• 背景问题：在推理阶段，由于每次只输入一个样本而不是一个小批次的数据，无法像训练时那样依赖于小批次内的统计量
• 解决方法：采用在训练过程中通过指数加权平均积累下来的全局均值和全局方差来进行归一化处理
  • 对于均值：
    $${\mu }_{\text{running}}=\beta \cdot {\mu }_{\text{running}}+(1-\beta )\cdot {\mu }_{\text{batch}}$$
  • 对于方差：
    $${\sigma }_{\text{running}}^2=\beta \cdot {\sigma }_{\text{running}}^2+(1-\beta )\cdot {\sigma }_{\text{batch}}^2$$
    $\beta$ 是一个超参数，称为动量（momentum），用于控制历史信息的重要性。通常情况下，$\beta$ 的值接近但小于1，比如0.9或0.99。

3.2. 线性变换的偏置可去除

• 深度学习实际使用通常是：线性变换 --> Batch Normalization（BN归一化）–> 激活函数

• 线性变换（例如，深度学习里面的卷积操作）：

  • 实现：主要通过矩阵乘法实现，其中输入数据与权重矩阵相乘，并加上偏置项（bias）。
  • 数学上：如果输入为 $x$，权重矩阵为 $W$，偏置为 $b$，则线性变换的结果为：
    $$z=Wx+b$$

• 批量归一化：输入首先会被标准化（减去均值后除以标准差），然后通过两个可学习参数进行调整。 如果在卷积层之后紧接着应用Batch Normalization，因为会减去均值，这样计算也会减掉卷积层里的偏置，那么卷积层的偏置项就变得多余了。

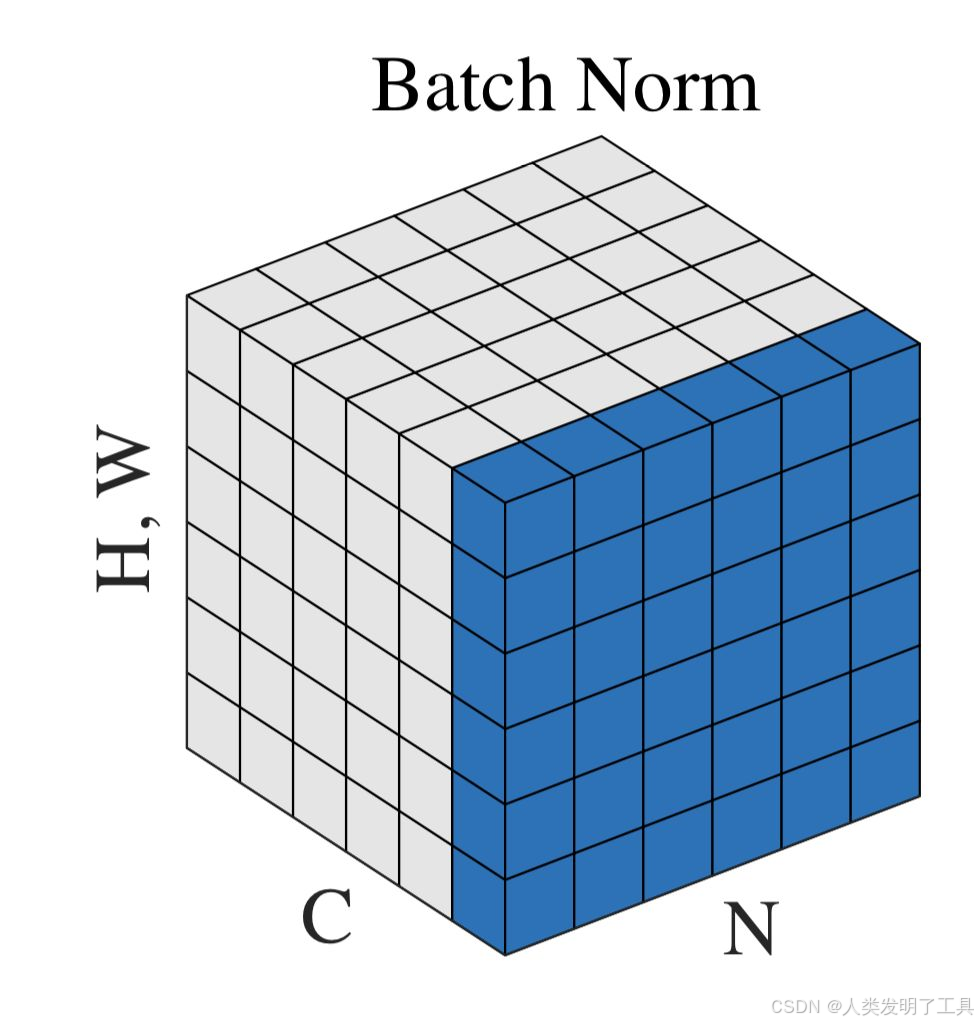
3.3. 每个通道对所有样本进行归一化

1. 计算方式：每个通道内的所有样本计算均值和方差
2. 学习参数量：因为每个通道有一个均值和方差，如果有6个通道维度，则有6组学习参数。