KMP—找出字符串中第一个匹配项的下标

1题目

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回 -1 。

示例 1：

输入：haystack = "sadbutsad", needle = "sad"

输出：0

解释："sad" 在下标 0 和 6 处匹配。

第一个匹配项的下标是 0 ，所以返回 0 。

示例 2：

输入：haystack = "leetcode", needle = "leeto"

输出：-1

解释："leeto" 没有在 "leetcode" 中出现，所以返回 -1 。

2链接

题目：28. 找出字符串中第一个匹配项的下标 - 力扣（Leetcode）

视频：帮你把KMP算法学个通透！（求next数组代码篇）_哔哩哔哩_bilibili

3解题思路

3.1暴力求解法

模式串needle和文本串haystack对齐开头，i指向haystack，j指向needle。

两层for循环遍历，needle和haystack出现某一位不匹配时，结束匹配，i++进入下一轮循环。

本质就是把needle字符串依次右移，直到和haystack完全匹配成功，返回haystack中匹配成功的子字符串下标

3.2KMP算法

3.2.1求前缀表

首先了解什么是前后缀

前缀：不包含最后一个元素的所有子字符串

后缀：不包含第一个元素的所有子字符串

举例：字符串aabaabaaf

前缀：a，aa, aab, aaba, aabaa, aabaab, aabaaba, aabaabaa

后缀：f, af, aaf, baaf, abaaf, aabaaf, baabaaf, abaabaaf

什么是前缀表：记录下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。前缀表储存的是最大相等前后缀长度。前缀表的任务是当前位置匹配失败，找到之前已经匹配上的位置，再重新匹配，此也意味着在某个字符失配时，前缀表会告诉你下一步匹配中，模式串应该跳到哪个位置。

以字符串aabaaf为例:

子字符串	前缀	后缀	前缀表
a	0	0	0
aa	a	a	1
aab	a, aa	b, ab	0
aaba	a, aa, aab	a, ba, aba	1
aabaa	a, aa, aab, aaba	a, aa, baa, abaa	2
aabaaf	a, aa, aab, aaba, aabaa	f, af, aaf, baaf, abaaf	0

3.2.2前缀表如何工作的

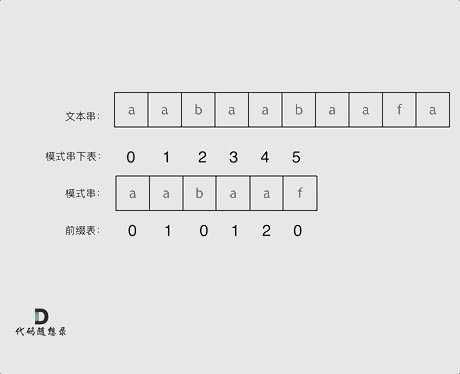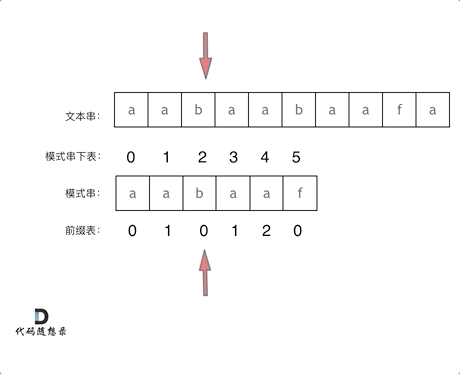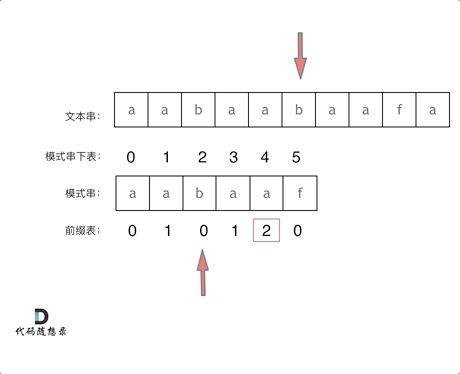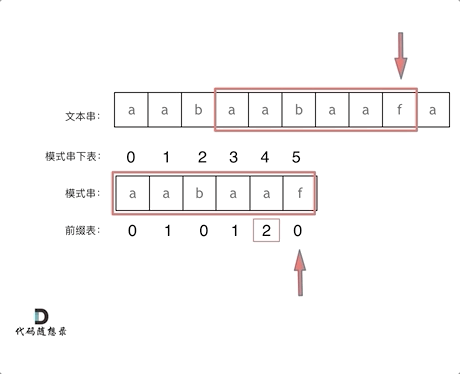
找到的不匹配的位置时要看它的前一个字符的前缀表的数值，因为要找前面字符串的最长相同的前缀和后缀，所以要看前一位的前缀表的数值。

前一个字符的前缀表的数值是2， 所以把下标移动到下标2的位置继续比配。 这样就保证文本串的指针不用回退，继续往后匹配了。

前缀表与next数组有什么关系

前缀表求出来是固定的，但是next数组不同的人由不同的写法

以前缀表0，1，0，1，2，0为例，可能出现以下常见next数组

1. 0，1，0，1，2，0 （按照前缀表构造next，不做变化）

2. -1，0，1，0，1，2 （把前缀表右移1位，初始位置为-1）

3. -1，0，-1，0，1，-1 （把前缀表统一减1）

这写变形不涉及到KMP的原理，而是具体实现，next数组既可以就是前缀表，也可以是前缀表统一减一（右移一位，初始位置为-1）。

4代码

//暴力求解，时间复杂度O(nm)
class Solution {
public:
    int strStr(string haystack, string needle) {
        int n = haystack.size();
        int m = needle.size();
        for (int i = 0; i + m <= n; i++) { //注意截止标志是i + m <= n
            int flag = true;//设定比对标志，当出现不匹配元素时置为false
            for (int j = 0; j < m; j++) {
                if (haystack[i + j] != needle[j]) { //如果出现字符不匹配
                    flag = false; //匹配标志位置为fale
                    break; //退出本轮关于needle的for循环，并通过i++进行后错位再匹配
                }
            }
            if (flag) { //如果在下标为i的一轮中全部匹配成功，flag未被置为false
                return i; //返回元素下标，且无需后续再匹配
            }
        }
        return -1; //匹配失败，返回-1
    }
};

//KMP算法
class Solution {
public:
    void getNext(int* next, const string& s) { //寻找字符串s的next数组
        int j = 0; //j代表着i和i之前字符串包含的最大相同前后缀长度，即next数组要记录的值
        next[0] = j; //next数组初始化为0，因为仅一个元素时定义的最大相同前后缀长度为0
        //用i遍历字符串，注意j从0开始i从1开始比对
        for (int i = 1; i < s.size(); i++) {
            while (j >= 1 && s[i] != s[j]) {
                //如果比对失败，j要回退到失败元素的前一个元素对应next表储存的下标处
                //j-1就是失败元素的前一个元素，next[j-1]就是对应储存的值
                //例如aabaaf, 某一次匹配失败next[j-1]=2，j就要回退到下标为2处'b'重新比对
                j = next[j - 1];
            }
            if (s[i] == s[j]) {
                j++; //如果比对成功，j就加1
            }
            //每一轮for循环，比对成功就j++，把j储存在next中，然后i++进入下一轮循环
            next[i] = j; 
        }
    }

    int strStr (string haystack, string needle) {
        if (needle.size() == 0) return 0; //模式串长度为0时，返回下标0
        int next[needle.size()]; //设置next数组的长度，等于模式串长度
        getNext(next, needle); //获取needle模式串的next数组
        int j = 0; //needle模式串用j遍历
        //用i来遍历haystack文本串
        for (int i = 0; i < haystack.size(); i++) {
            //如果模式串第j位和字符串第i位不匹配
            while (j > 0 && haystack[i] != needle[j]) {
                //模式串遍历指针j依据next数组回退，while循环，若不匹配一直回退直到j变为0
                //j对应的的下标回退到前一位元素对应next的数值处
                j = next[j - 1]; 
            }
            if (haystack[i] == needle[j]) {
                j++; //如果字符串和模式串匹配，本轮for循环结束，i和j均加1右移
            }
            //如果j遍历完模式串结尾，说明全部匹配完成
            //注意j是下标，j == needle.size()说明j都指向needle结束的后一位了
            if (j == needle.size()) { 
                return (i - j +1); //返回此时文本串符合要求子字符串的开始下标
            }
        }
        return -1; //未匹配到满足要求的字符串，返回-1

    }
};