[日记]LeetCode算法·一——数组

1 二分查找

• 二分查找注重于区间的清晰定义，我采用[left,right)进行定义每一个区间。
• 二分查找适用于有序（升序）+无重复的数组。

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left=0;
        int right=nums.size();
        while(left<right)
        {
            int mid=(left+right)/2;
            if(nums[mid]==target)
                return mid;
            else if(nums[mid]<target)
                left=mid+1;
            else
                right=mid;
        }
        return -1;
    }
};

2 移除元素

• 最简单的想法是直接利用后值进行覆盖，每一次遇到删除值，将后续所有数组向前挪1位。
• 事实上，由于元素顺序可以改变，因此可以采用双指针进行操作。
• 思路很简单，直接利用Left和Right两个指针，不停地将Right指针处的非删除元素替换Left指针处的待删除元素，直到两指针错开。

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        //因为元素顺序可以改变，所以可以采用双指针法
        int left=0;
        int right=nums.size()-1;

        while(left<=right)
        {
            while(left<=right && nums[left]!=val)++left;
            while(left<=right && nums[right]==val)--right;

            if(left<=right && nums[left]==val)
            {
                nums[left]=nums[right];
                left++;
                right--;
            }
        }

        return left;
    }
};

3 有序数组平方

• 由于原数组自带了升序信息，因此可以推测出平方后的数组也一定与原数组顺序有相关性，显然，最大平方数来源于最小的负数或最大的正数，因此采用头尾两端的双指针就可以直接获得平方后的正确数组顺序。
• 先采用降序进行排列，之后倒置即可。

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        vector<int> result;
        int left=0;
        int right=nums.size()-1;
        while(left<=right)
        {
            int sqr_left=nums[left]*nums[left];
            int sqr_right=nums[right]*nums[right];

            if(sqr_left<sqr_right)
            {
                result.push_back(sqr_right);
                right--;
            }
            else
            {
                result.push_back(sqr_left);
                left++;
            }
        }

        reverse(result.begin(),result.end());
        return result;
    }
};

4 长度最小子数组

• 显然，求得长度最小的连续子数组，实际上就是维护一个满足sum>=target的动态区间，并记录其区间长度。
• 那么自然地，利用双指针，维护该动态区间的头尾两端，每当从右侧加入一个元素使得该区间满足条件之后，尝试尽可能地将左侧的元素删去以维持最小的区间，并且实时更新最小长度，直到该区间不再满足条件，进行下一个右侧元素的加入。

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int left=0;
        int right=0;
        int minlength=nums.size()+1;
        int curlength;
        int cursum=0;

        for(right=0;right<nums.size();++right)
        {
            cursum+=nums[right];
            while(cursum>=target)
            {
                curlength=right-left+1;
                minlength=min(curlength,minlength);
                cursum-=nums[left++];
            }
        }

        return minlength==nums.size()+1?0:minlength;
    }
};

5 螺旋矩阵II

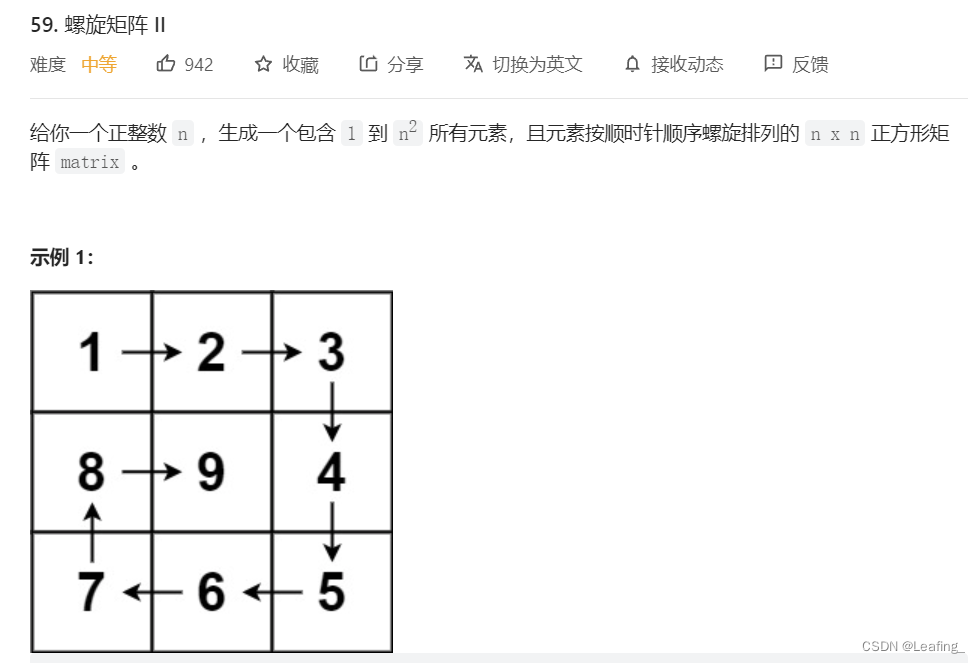
没什么好说的，想清楚每一次循环的起点与终点即可，另外考虑到奇数与偶数的差异。

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> mat(n, vector<int>(n, 0));
        //环数
        int num_ring=(n+1)/2;
        //目前该填的数字
        int cur_num=1;
        //坐标
        int i,j;
        //每一圈进行循环
        for(int k=0;k<num_ring;k++)
        {
            //→
            i=k;
            for(j=k;j<n-k-1;j++)
                mat[i][j]=cur_num++;
            //↓
            j=n-1-k;
            for(i=k;i<n-k-1;i++)
                mat[i][j]=cur_num++;
            //←
            i=n-1-k;
            for(j=n-1-k;j>k;j--)
                mat[i][j]=cur_num++;
            //↑
            j=k;
            for(i=n-1-k;i>k;i--)
                mat[i][j]=cur_num++;
        }
        //最后n为奇数时，最中心处填入n*n
        if(n%2==1)mat[n/2][n/2]=cur_num;
        return mat;
    }
};

6 总结

数组是相对比较简单的数据结构，其特点是在内存上的连续分布，这使得其的查询十分便利，但缺点是由于连续的内存分布，在删除和插入上都有着不可避免的繁琐之处。
对于有序数组，往往需要利用其有序性进行算法的优化，必要时双指针、三指针都可以有效地维护实际需要处理区间范围。
——2023.2.15