0.1 + 0.2 不等于0.3 问题，精度的丢失和解决办法

10个0.1相加不等于1；

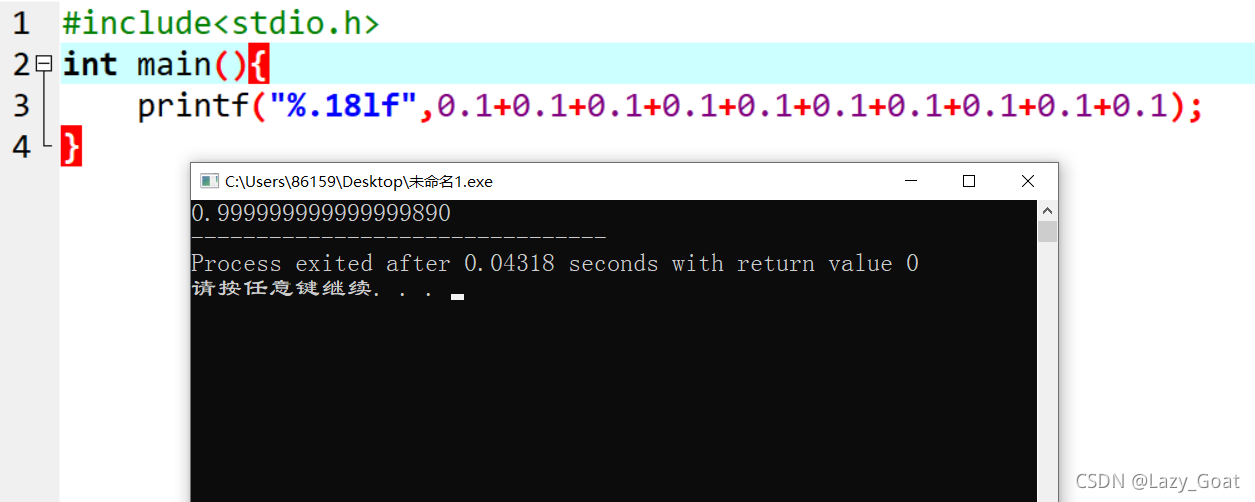
这是因为浮点数精度丢失的问题，首先知道在计算机中数字是以二进制的方式存在的，那么在CPU中计算0.1+0.1时实际上是0.1的二进制的相加；
（ 0.1 => 0.0001 1001 1001 1001…无限循环）
如上，因为是无限循环，所以CPU计算时不会存储太多位，因此会在某位初截断。
根据IEEE-754标准，最大保留0.1后小数点后17位也就是这样：

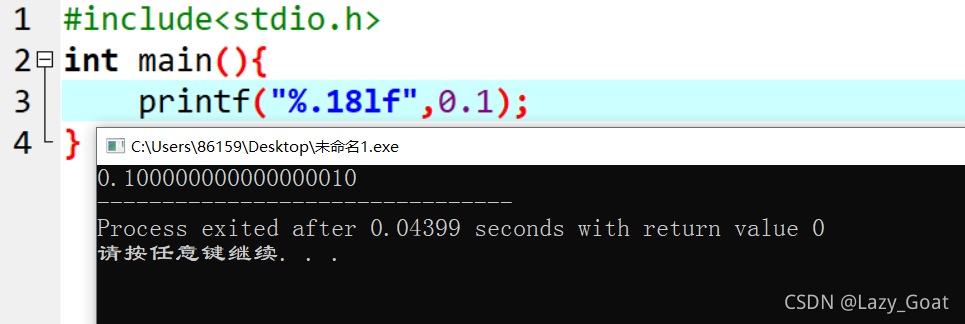
所以也就有在编程环境中把1分成三份，再加起来就不再是1了。同样0.1+0.2也就不等于0.3了。

IEEE-754标准中一个浮点数分成两部分组成： $$6.4\ast 10^6$$

第一部分位数也叫做有效数字；
第二部分指数；第三部分符号位表示正负；
指数和尾数分开存储也就符合科学计数法的计数方法，那么他就可以表示很多，大到天文数字，小到微粒半径；

在我们十进制中可以用0.1来精确地表示十分之一，但是在计算机中存储0.1是使用二进制，他们之间的差别在于：
十进制：

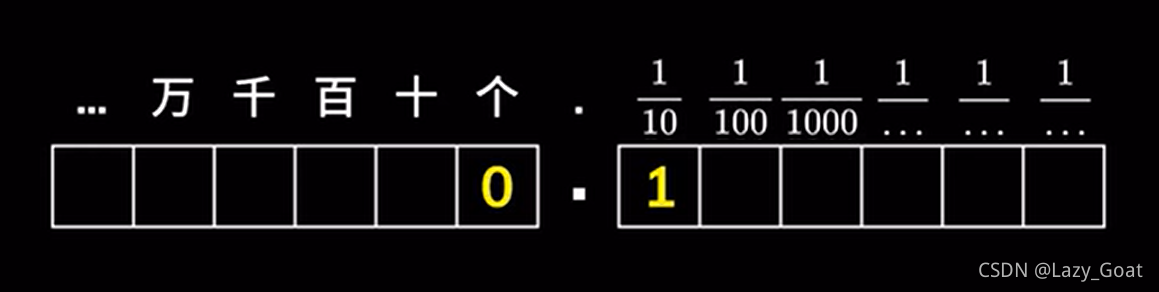
在小数部分我们可以用零点几来精确的表示我们想要表达的小数。但是却没有三分之一

二进制：

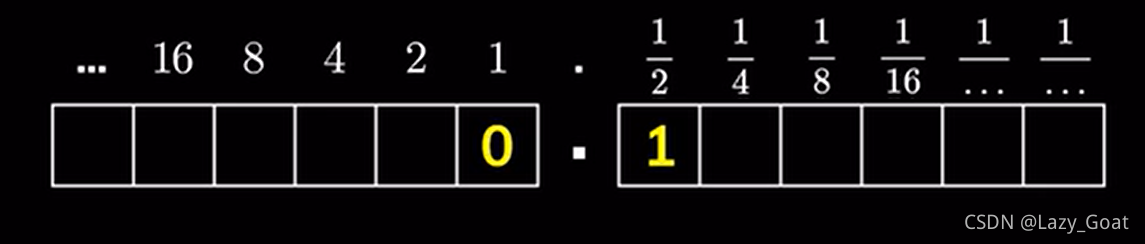
在二进制中，我们可以轻易的表示二分之一、四分之一、四分之三等等，但是没有十分之一，我们可以轻易的发现其中的差别。

二进制中表示十分之一就会是这样0011会移植循环下去：

但是计算机无法存储无线循环小数，我们使用的32位浮点数单精度数float只有23个有效数字，那么我们的小数在23位之后就会被截断了。所以计算机在表示0.1时就已经丢失了精度。

那么在二进制中存在精度丢失的问题，在十进制中也存在这样的问题：
比如三分之一：0.3333333333333333333333333333333333

但是我们只能保留有限位数字，所以必定会在某一位后将其截断，然后会丢失精度。
所以在计算:
$$1/3+1/3+1/3$$
的答案非常接近一但却不等于一。

虽然在二进制中并不能总是精确地表示小数，但是在大多数情况下并不是问题。

但是在银行中怎样存储0.1元呢？如果精度丢失对于银行岂不是要亏损。
那么使用100表示一块钱就可以解决精度丢失的问题。

在编程环境中怎样避免精度丢失的问题呢？
在大多数编程语言中有一个Decimal(‘number’)，可以使用它来表示任意精度的浮点数，用它来计算浮点数不会出现任何问题。
如在python中:

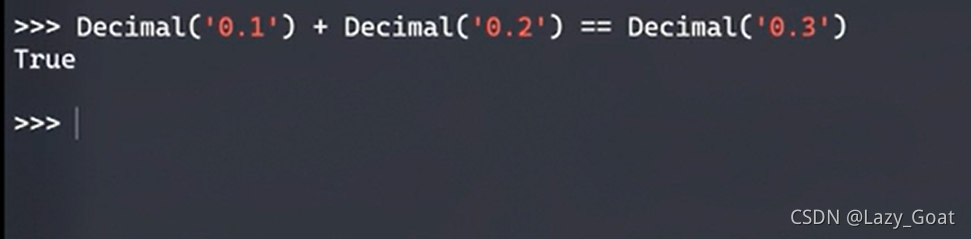
但是在大多数的时候，我们依然会用到浮点数，因为浮点数运算的特点：效率高、运算快、节省内存空间的优点。那么怎样判断两个浮点数是否相等。
这样的操作是很不可靠的：如python中

那么应该怎样做。正确的做法是去计算这两个数的差别是否小于某个误差范围，常用的误差范围是十的负六次方，如在Python中:

这样从逻辑上判断两个浮点数相等，从而避免逻辑上的误区。
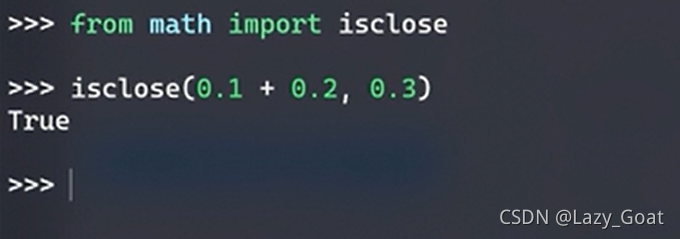
在很多编程环境中都内置了判断浮点数是否相等的函数，如Python中的isclose()：