理解
滑动窗口本质是双指针的一种应用,但比普通双指针更有明确的 “区间约束”。(双指针的一个子集+具体化)
滑动窗口是处理数组 / 字符串子问题的高效技巧。核心结论是:滑动窗口通过维护一个动态变化的 “窗口”(子区间),将暴力解法的 O (n²) 时间复杂度优化到 O (n),适用于解决子数组 / 子串的求和、计数、匹配等问题。
滑动窗口是在数组或字符串上维护的一个连续子区间,用两个指针(左指针 left、右指针 right)界定范围。窗口的 “滑动” 体现在指针的移动:右指针扩大窗口范围,左指针缩小窗口范围,通过动态调整窗口来满足题目条件,避免重复计算。
实战例题
leetcode209例题

算法原理讲解:
解法一:暴力枚举
枚举每一个数组,然后计算它的和,是否满足>=target
枚举每一个数组就是固定left指针,然后移动right指针,时间复杂度O(N^2)
然后枚举完之后计算sum,时间复杂度一共就会变成O(N^3)
优化:枚举的时候顺便计算sum,这样就会使时间复杂度O(N^2)
再优化的过程当中我们发现解法二

比如数组{2,3,1,2,4,3}
注意题目都是正整数,所以我们每次+一个数的时候,sum都会变大,所以sum是单调递增的
解法一暴力枚举的时候,当我们发现从左+到右,当sum>7的时候,right就没必要往右边+了。因为是正整数,你在往右边+,sum必然>7,len也在变大,所以此时固定left,right++的数组已经找到len最小的情况了
而且当我们right++到合适位置了之和,left++寻找下一组数组,left++的时候right不用回退到left的位置,因为前面一段区间的sum我们已经计算过了,当你left++的时候,
我们仅仅需要sum-nums[left]就能够算出left++,right合适的这段区间的新的sum了,新的sum只会<=target,不会大于,所以right是不会--的
这就是滑动窗口(类似于一个窗口再移动),利用了单调性,规避了很多没必要的枚举,也就是left和right都是从左往右再移动(同向指针),不会回退
举个例子:
固定left指针(出窗口)指向2,一开始移动right(进窗口)指针,从2开始移动
right指向2,2进窗口,sum=2,len=1,判断sum<target
right++,指向3,3进窗口,sum=5,len=2,判断sum<target
right++,指向1,1进窗口,sum=6,len=3,判断sum<target
right++,指向2,2进窗口,sum=8,len=4,判断sum>target
此时符合条件,那就算一个结果
然后left++,指向3,2出窗口,sum=8-2=6,len=3,判断sum<target
right++,指向4,4进窗口,sum=10,len=4,判断sum>target
所以也是符合一组
注意这里的更新结果是可能再进窗口的时候,也可能判断结果,具体的更新结果是根据题意来判断,这里把更新结果放在判断结果后面,判断完之后我们要更新完长度和sum才能出窗口
时间复杂度O(2N),即O(N)
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int n = nums.size();
int left = 0;
int right = 0;
int sum = 0;
int len = INT_MAX;
while (right < n) {
sum += nums[right];
while (1) {
if (sum >= target) {
len = min(len, right - left + 1);
sum -= nums[left++];
} else {
right++;
break;
}
}
}
if (len == INT_MAX)
return 0;
return len;
}
};
leetcode3例题

算法原理讲解:
解法一:暴力枚举+hash判定是否重复
例如”abcabcbb“
left从a开始,right从a开始,right++,一直到abca发现重复,所以就是abc
left从b开始,right从b开始,right++,一直到bcab发现重复,所以就是bca
以每个字符开头,枚举发现是否重复,然后统计出最大的len,返回即可
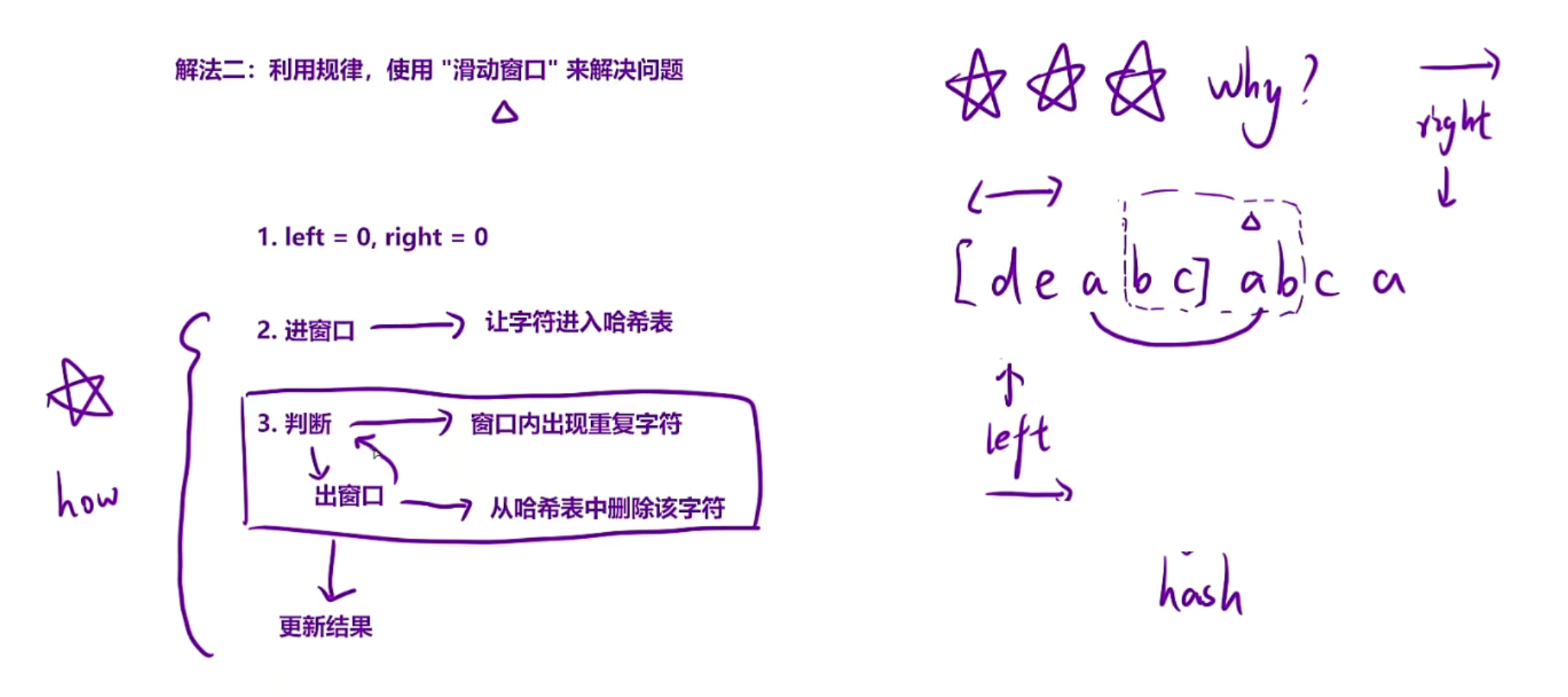
当我们发现枚举的时候,例如“deabcabca”
left指针指向d,right指针指向d,然后right++,一直到a发现重复,所以此时len=deabc
下一轮移动的时候,left指向的是第一个a的下一个位置,right指向的是第二个a
思考为什么可以这样?(right不用回退?left和right都是从左往右移动(滑动窗口))
如果你left指向e,而不是第一个a的下一个位置,那它还是重复的,right不用回退是因为前面已经能够保证这一段不是重复的了,所以从第二个a开始就行
做滑动窗口的题目不是知道使用滑动窗口的前提下编写代码,代码很简单,主要理解为什么使用滑动窗口,为什么right不回退,为什么left和right都是从左往右移动
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int left = 0;
int right = 0;
int len = 0;
int n = s.size();
int hash[256] = {0};
for (; right < n; right++) {
int ret = s[right];
hash[ret]++;
while (hash[ret] > 1) {
// 出现重复
hash[s[left++]]--;
}
len = max(len, right - left+1);
}
return len;
}
};
leetcode1004例题

算法原理讲解:
题目说最多可以翻转k个0,不是说只能恰好,所以可以翻转<=k个0
其次如果按翻转来做,代码书写和思维都比较难,需要翻转之后再记录1的个数
我们可以把题意理解为寻找一个子数组,子数组中0的个数<=k个
解法一:暴力枚举+zero计数器
也就是固定left,然后right往右移动,依次枚举每个子数组中0的个数
解法二:滑动窗口
在暴力枚举中我们发现可以优化
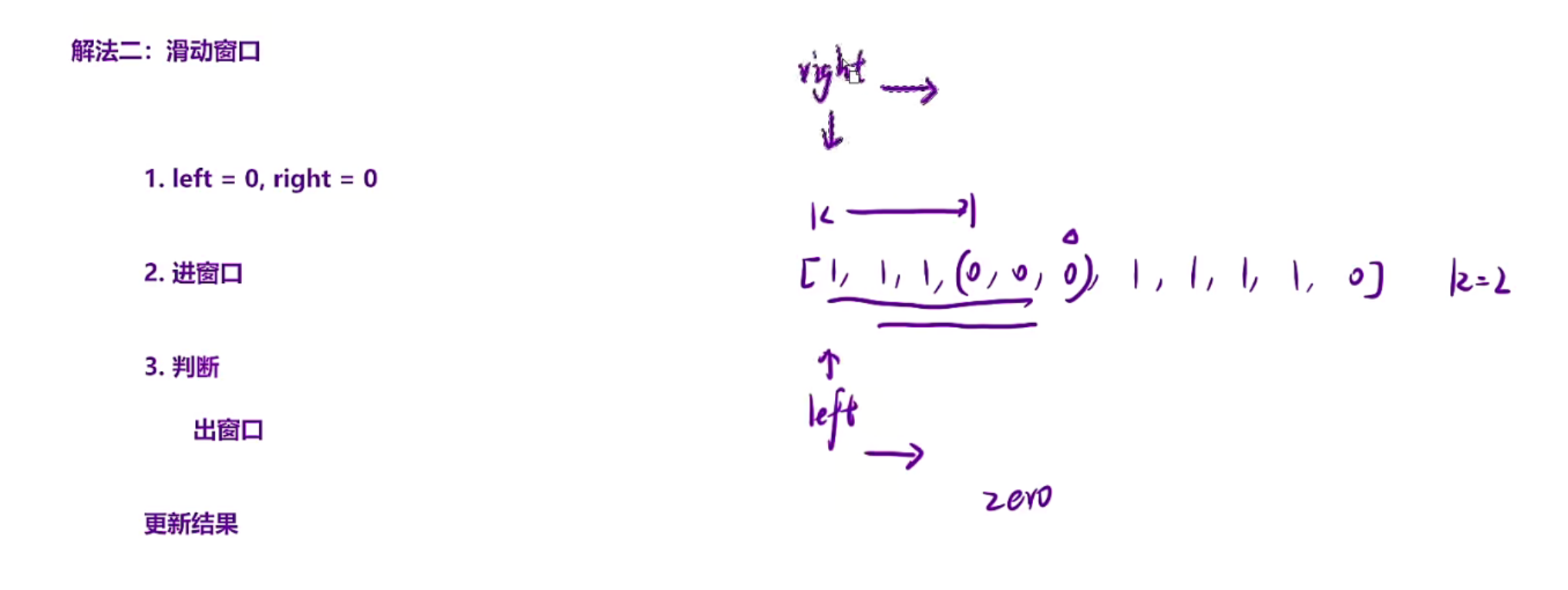
比如数组{1,1,1,0,0,0,1,1,1,0}
当固定left指针的时候,枚举子数组时,我们发现当枚举到第二个0的时候,刚好符合题意k=2,此时接着往下枚举,发现下一个是0,那就超过了,没必要往下枚举了,此时记录len为right-left
正常的暴力枚举是移动left,然后right回来和left同时指向一个位置,然后right++,一直往后枚举,但是此时我们发现如果left指向第二个1,right从第二个1开始往后的时候和第一种情况一样,也是枚举到3个0那里结束,所以优化就是不需要left++,而是直接跳过这一堆1,跳过1个0,让0的个数<=k,此时往后枚举的子数组才有意义,而且发现right不用回来,回来了也一样,因为我们知道了zero的个数,直接--就行,不用回是因为这一段区域由于left跳过了一定个数的0,所以导致left-right这段区间是合法的,right直接往后面找就行
因为left和right都是从左往右,并且right在left前面不回退
所以使用滑动窗口的解法
class Solution {
public:
int longestOnes(vector<int>& nums, int k) {
// 问题转换:让子数组中0的个数不超过k个
int left = 0;
int right = 0;
int n = nums.size();
int len = 0;
int zero = 0;
while (right < n) {
// 进窗口
if (!nums[right]) {
zero++;
}
// 出窗口
while (zero > k) {
if (nums[left] == 0) {
zero--; // 左移移除0,减少计数
}
left++; // 无论移除的是0还是1,都要移动左指针
}
// 更新结果
len = max(len, right - left + 1);
right++;
}
return len;
}
};
leetcode1658例题

class Solution {
public:
int minOperations(vector<int>& nums, int x) {
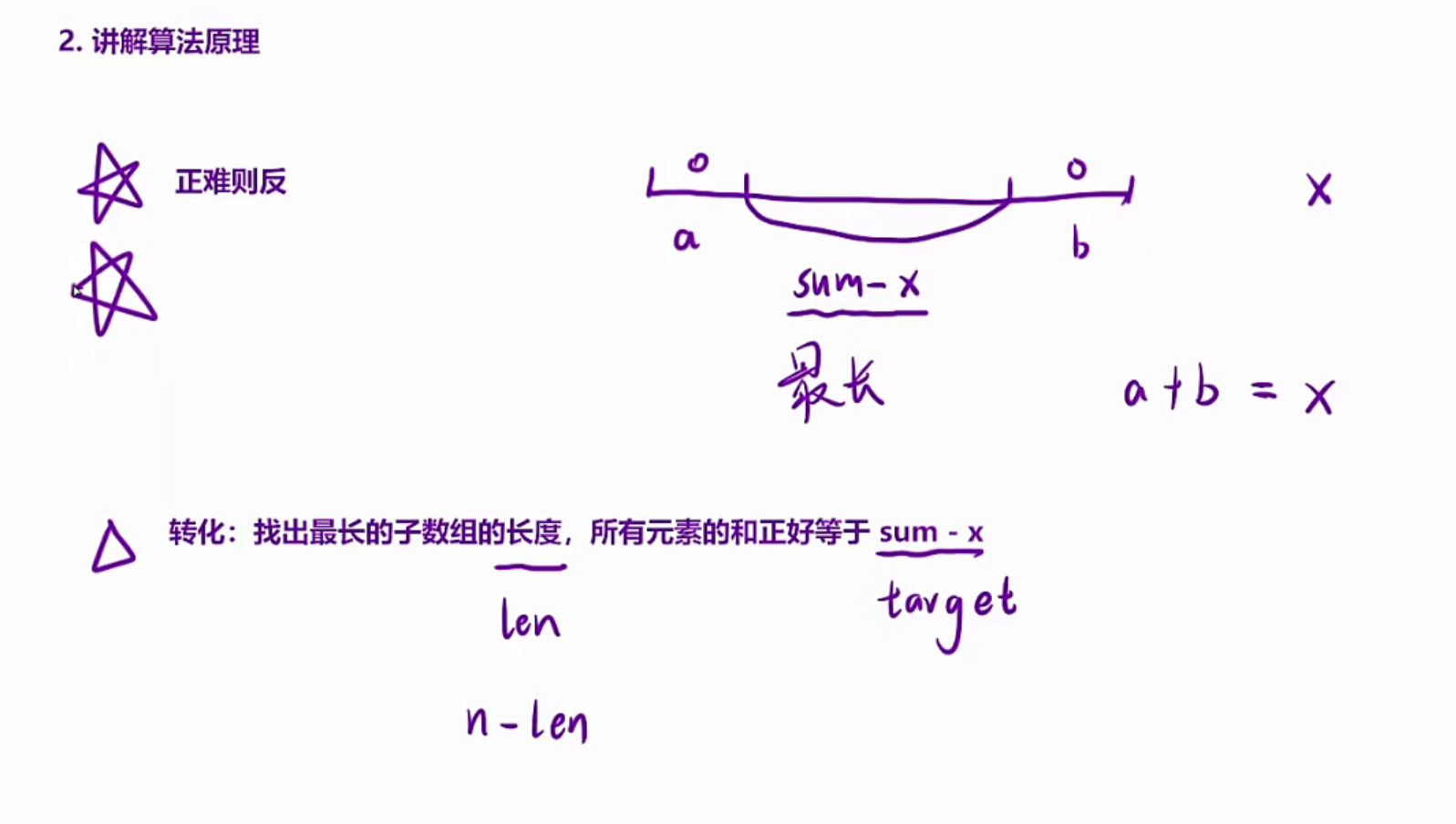
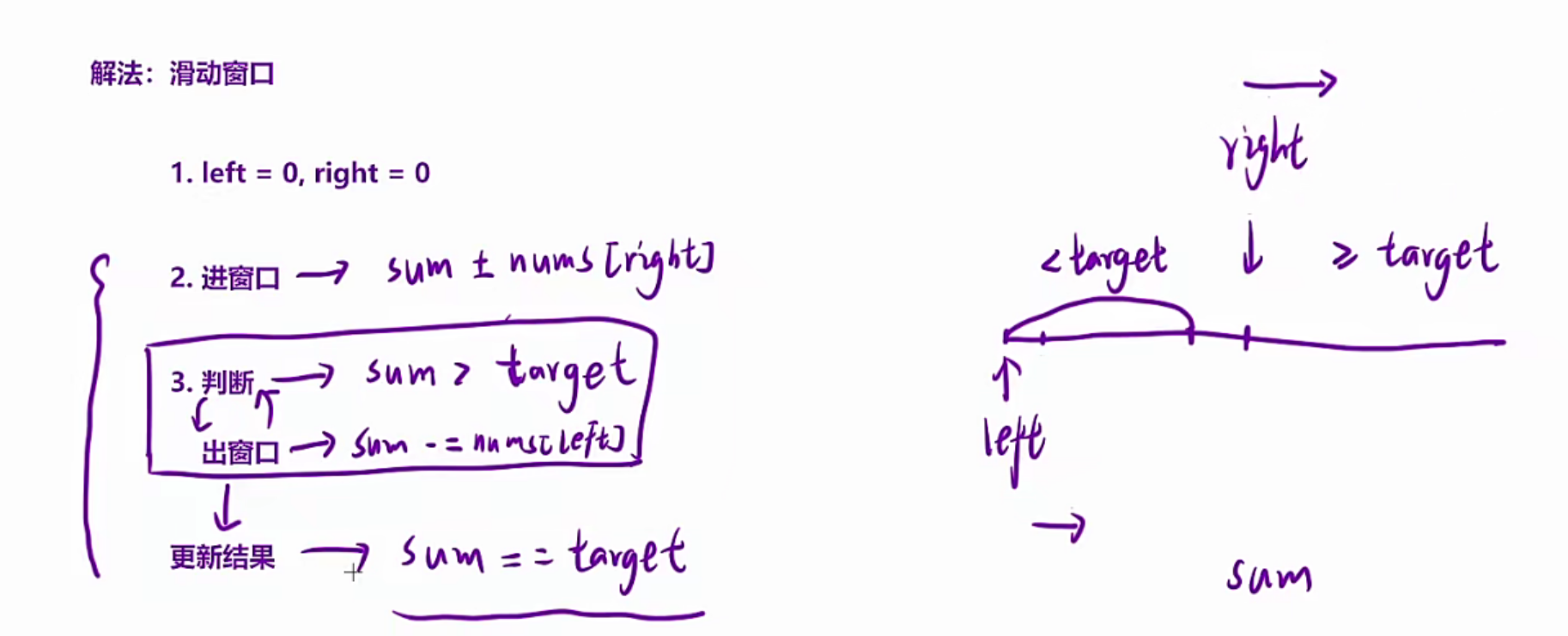
// 正难则反:找一个区间,让其和为sum-x
int left = 0;
int right = 0;
int n = nums.size();
int sum = 0;
for (int i = 0; i < n; i++) {
sum += nums[i];
}
int target = sum - x; // 找区间让其和=target;
if(target<0)
return -1;
int len = -1;
int ret = 0; // 用来记录区间和
while (right < n) {
// 进窗口
ret += nums[right];
// 判断
while (ret >target&&left<=right) {
//出窗口
ret -= nums[left++];
}
if(ret==target)
{
len=max(len,right-left+1);
}
right++;
}
if(len==-1)
return len;
else return n-len;
}
};
leetcode904例题

算法原理讲解:读完题后,发现就是在一个数组当中寻找一个最长的子数组,子数组当中只有两种数字,做数组类的问题,一定要从暴力枚举当中寻找优化,先从暴力枚举解题
解法一:暴力枚举+hash
比如数组{1,2,3,2,2}
暴力枚举每一个数组,left和right同时指向1,然后right++,一直枚举子数组,发现right++到3的时候出现三种数字就没必要往下枚举了,在往下也是不符合的,枚举到12,长度为2
所以枚举下一组,left从2开始,right也从2开始,那就是枚举到2322,长度为4
枚举下一组left和right同时指向3,right++,那就是枚举到322,长度为3
依次这样枚举每一个子数组,找到其中最长的,这期间需要借助hash来判断是否有第三种元素
解法二:滑动窗口+hash
暴力枚举的时候发现,left枚举下一组的时候,right不用回退,left++的时候要么造成数字种类-1,要么数字种类不变,不会再增加,你right回退不回推都不影响,反而会增加时间复杂度,所以这符合滑动窗口的定义:left和right都是从左往右,然后right一直再left前面,窗口内一直保持一个特性
举一个例子在此理解,比如数组{1,2,1,2,3,2,3,3}
left和right同时指向1,进窗口就是hash[f[r]]++,也就是hash存的是<int,int>,然后判断一下,hash里面的数量是不是超过2,没有那就依次right++,然后加到3,发现hash中的元素种类超过了3,所以right暂停,left移动的时候要依次给hash里面元素种类的个数--,直到某个元素减到没,所以此时left是移动的第二个2的,也就是下图当中的left和right指向的样子
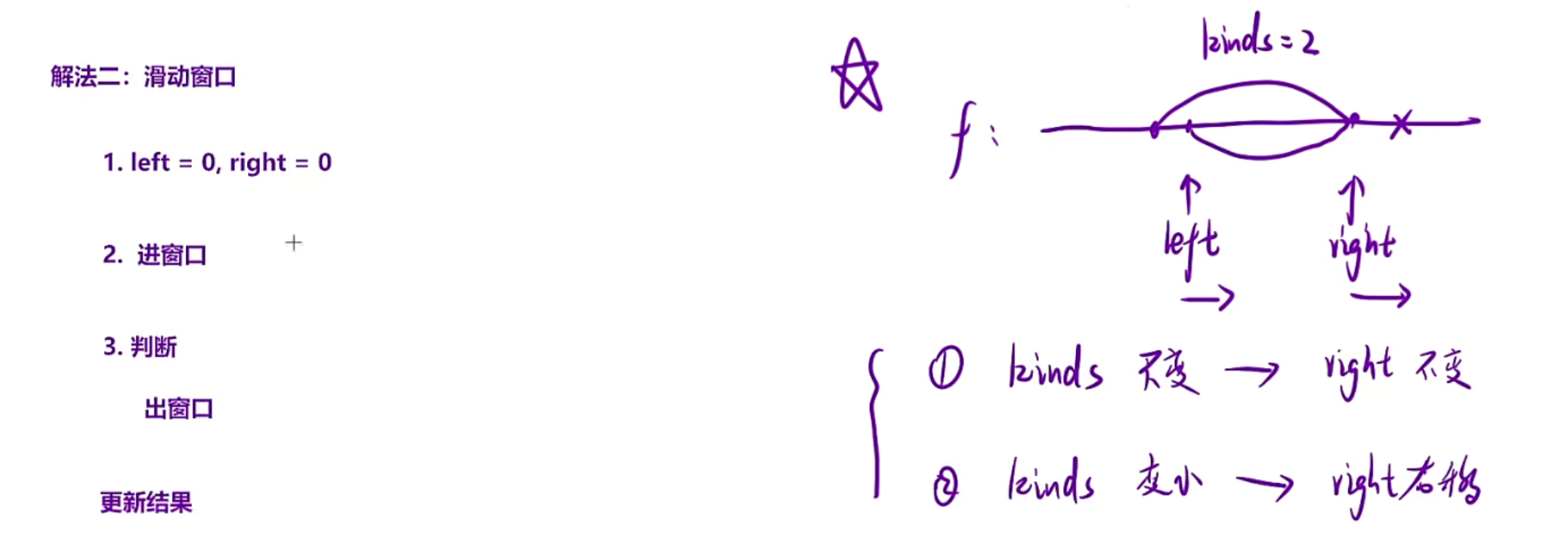
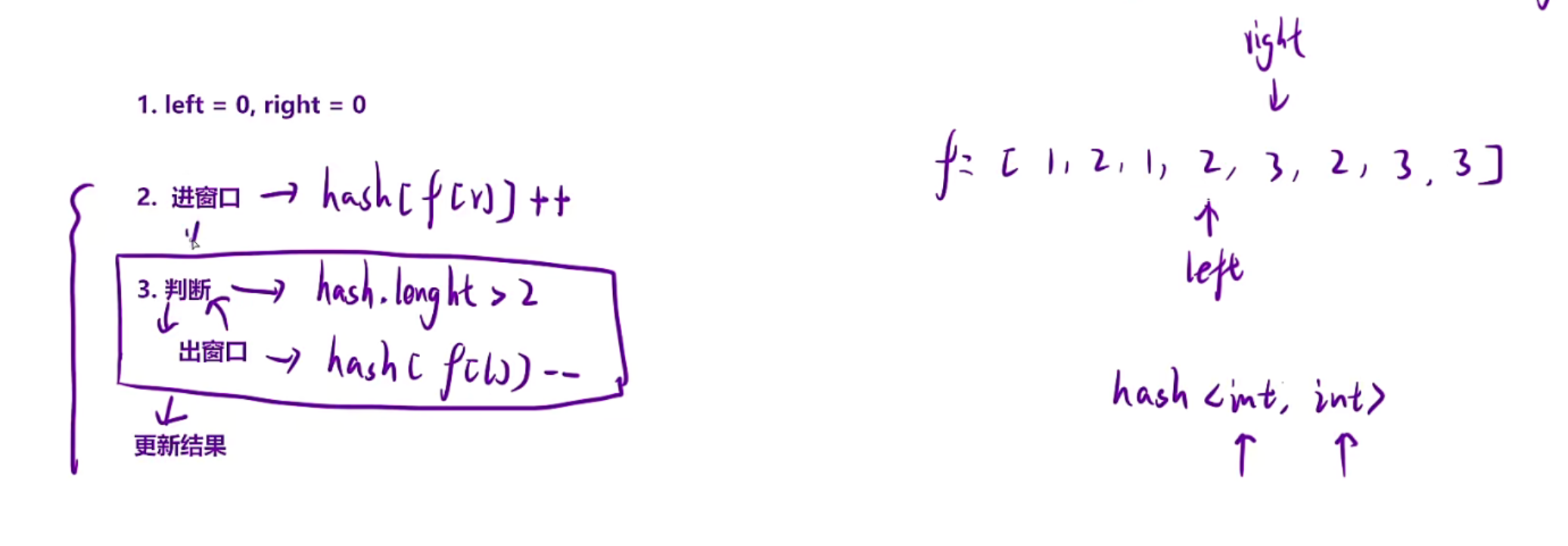
class Solution {
public:
int totalFruit(vector<int>& fruits) {
int left = 0;
int right = 0;
int n = fruits.size();
int len = 0;
unordered_map<int, int> hash;
while (right < n) {
hash[fruits[right]]++;
while (hash.size() > 2) {
// 此时有三个元素了
hash[fruits[left]]--;
if (hash[fruits[left]] == 0) {
hash.erase(fruits[left]);
}
left++;
}
len = max(len, right - left + 1);
right++;
}
return len;
}
};
leetcode438例题

算法原理讲解:异位词就是比如p为abc,那异位词就可以是abc,acd,bac,bca,cab,cba
解法一:暴力解法+hash
枚举每一个数组,但是此时我们发现子数组的长度肯定要和p的长度一样,才能称为异位词,所以枚举数组长度不能超过psize,所以这就有点像滑动窗口(固定版本)
解法二:滑动窗口+hash
滑动窗口大小就是psize大小,固定这个窗口大小,从左往右边扫,一样就记录下来
此时还需要配合hash,hash1记录窗口里面的状态,hash2是p字符串的状态,我们只需要比较hash中的元素是否相等,相等了之后元素个数是否一样,就能判断这两个是不是异位词
class Solution {
public:
template <typename Key, typename Value>
bool compareUnorderedMaps(const std::unordered_map<Key, Value>& map1,
const std::unordered_map<Key, Value>& map2) {
if (map1.size() != map2.size()) {
return false;
}
for (const auto& pair : map1) {
auto it = map2.find(pair.first);
if (it == map2.end() || it->second != pair.second) {
return false;
}
}
return true;
}
vector<int> findAnagrams(string s, string p) {
unordered_map<int, int> hash1;
unordered_map<int, int> hash2;
vector<int> v;
int psize = p.size();
int ssize = s.size();
int left = 0;
int right = psize - 1;
for (int i = 0; i < psize; i++) {
hash2[p[i]]++;
}
// 初始化第一个窗口(left=0到right=psize-1)
for (int i = 0; i < psize; ++i) {
hash1[s[i]]++;
}
// 检查第一个窗口
if (compareUnorderedMaps(hash1, hash2)) {
v.push_back(0);
}
// 滑动窗口:每次右移一位,高效更新哈希表
for (int i = psize; i < ssize; ++i) {
// 移除窗口最左侧的字符(i - psize 是左边界索引)
char leftChar = s[i - psize];
hash1[leftChar]--;
if (hash1[leftChar] == 0) {
hash1.erase(leftChar); // 计数为0时删除键,避免干扰比较
}
// 添加新的右边界字符(i是当前右边界索引)
char rightChar = s[i];
hash1[rightChar]++;
// 检查当前窗口(左边界索引为 i - psize + 1)
if (compareUnorderedMaps(hash1, hash2)) {
v.push_back(i - psize + 1);
}
}
return v;
}
};
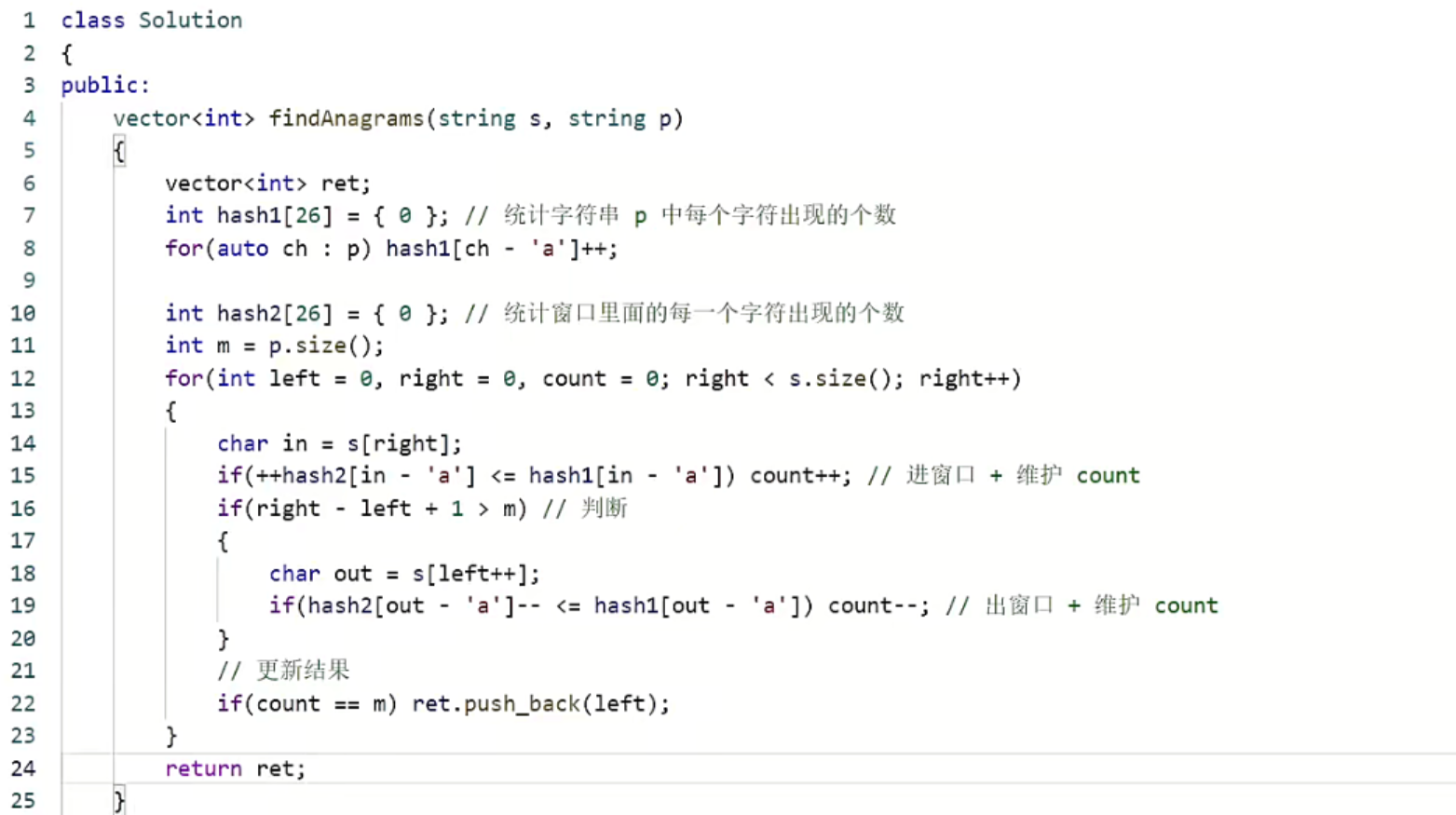
注意:这里题目当中的都是小写字母,所以我们可以用一个数组hash[26]来充当hash表
第二种写法:

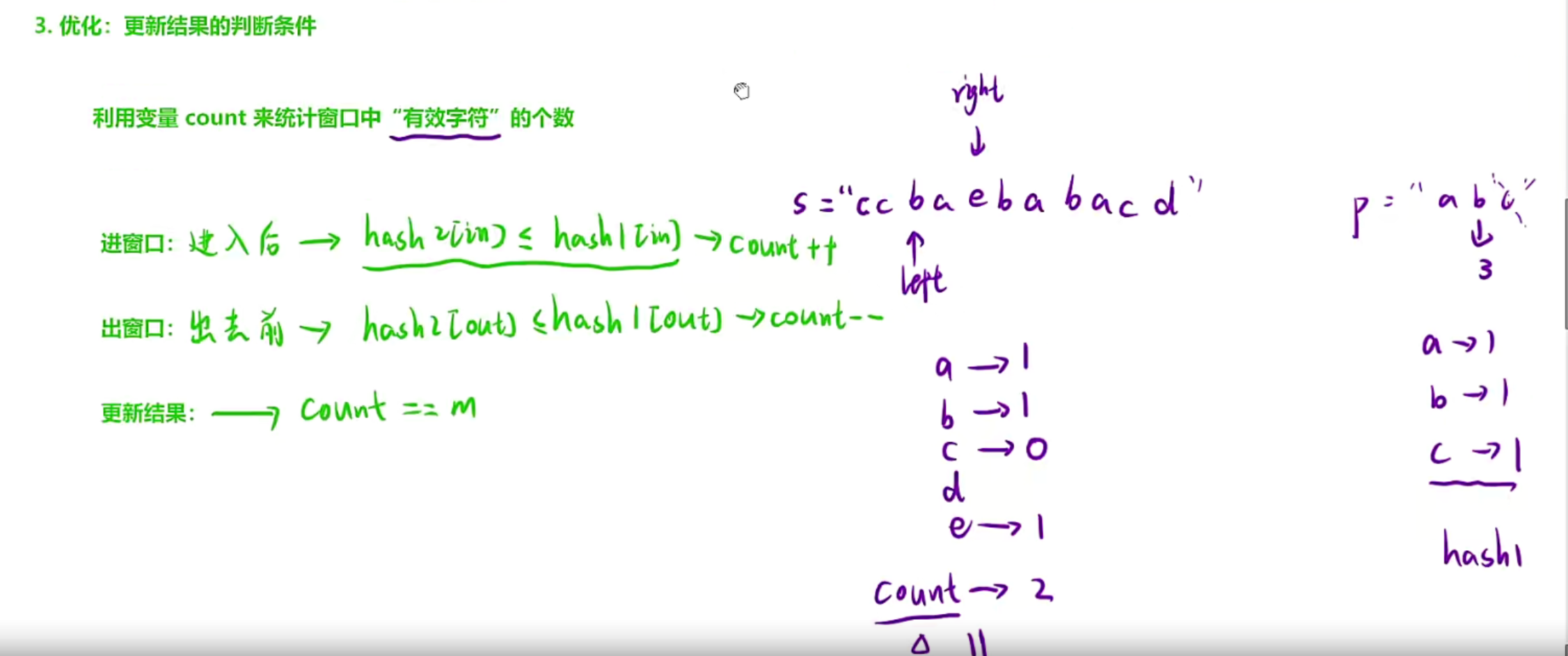
这是对于更新结果的优化(不需要再每次遍历一遍hash,而是维护一个计数器)
leetcode30例题

算法原理讲解:读完题会发现和之前的438题类似
转换:把word中的字符串看成一个个字符,比如foo可以整体看成a,bar整体看成b,然后s字符串中进行3个3个的划分bar就是b,然后foo就是a,其他第一次出现可以看成c、d
所以s字符串就变成了,bacabd,然后在这个字符串当中找ab的异位词,所以就是438题的变形
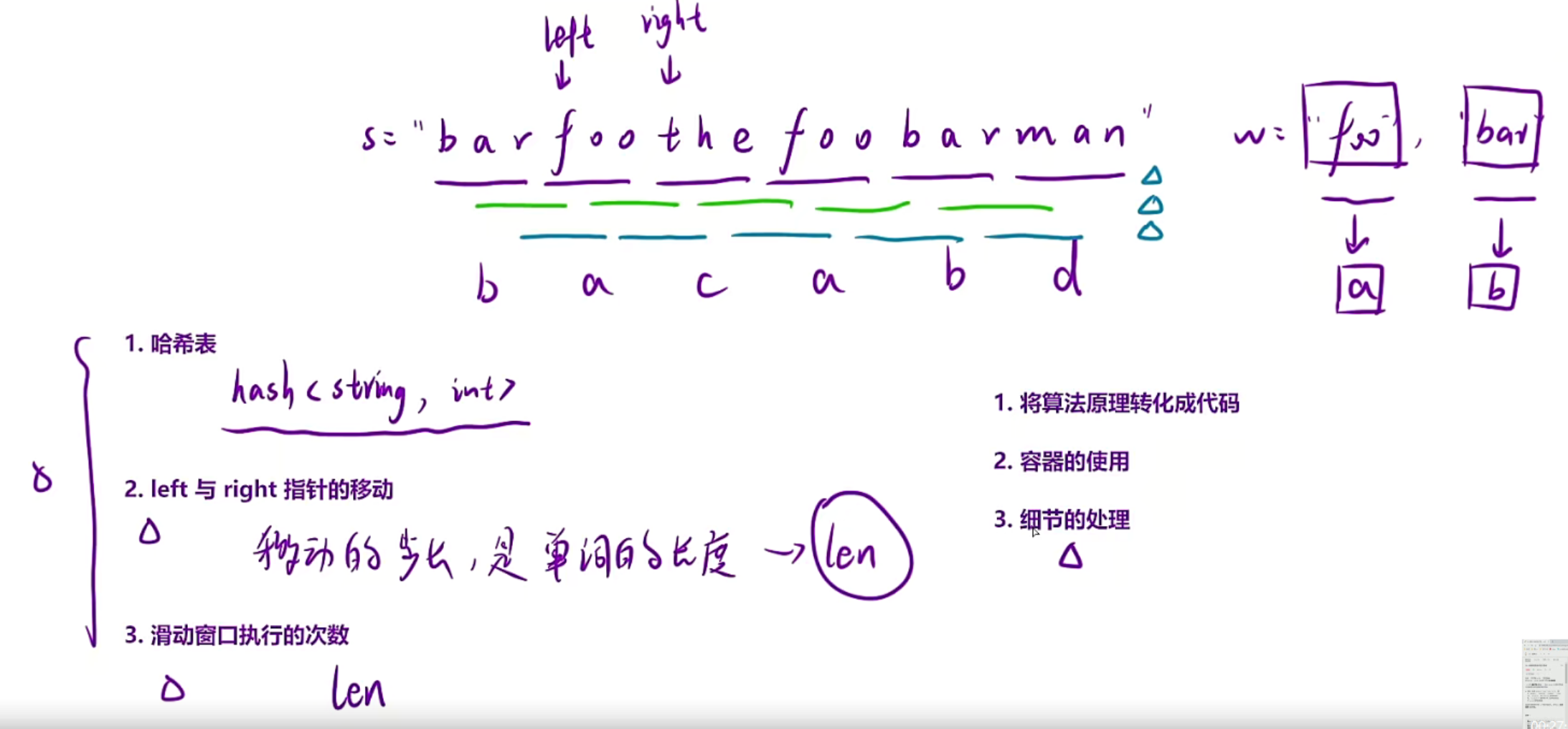
注意:这里我们进行滑动窗口的次数是len次,第一次是紫色线划分,第二次是绿色线,第三次是蓝色线
class Solution {
public:
vector<int> findSubstring(string s, vector<string>& words) {
unordered_map<string,int> hash1;//hash1用来存储words中的
vector<int> ret;
for(auto&ws:words){
hash1[ws]++;
}
//控制滑动窗口的次数
int len=words[0].size();
int m=words.size();
for(int i=0;i<len;i++){
//每次滑动窗口
unordered_map<string,int> hash2;//hash2用来存储s中的
int count=0;
for(int left=i,right=i;right+len<=s.size();right+=len){
//进窗口,维护count
string in=s.substr(right,len);
hash2[in]++;
if(hash1.count(in)&&hash2[in]<=hash1[in]){
count++;
}
//判断
if(right-left==len*m){
//出窗口
string out=s.substr(left,len);
if(hash1.count(out)&&hash2[out]<=hash1[out]){
count--;
}
hash2[out]--;
left+=len;
}
//更新结果
if(count==m){
ret.push_back(left);
}
}
}
return ret;
}
};
leetcode76例题

算法原理讲解:
解法一:暴力枚举+哈希表
做子数组一定要学会枚举,把所有的可能性枚举出来,在暴力当中寻找最优解
例如例1当中的字符串,我们以A开头枚举所有的,发现right走到C的时候结束,此时是最短的
以D开头枚举,枚举到下一个A的时候结束,此时是最短的
借助哈希表,如果hash2当中的每个元素的个数都>=hash1的才符合
把所有的情况枚举出来,然后返回符合条件最小的,时间复杂度O(N^2)
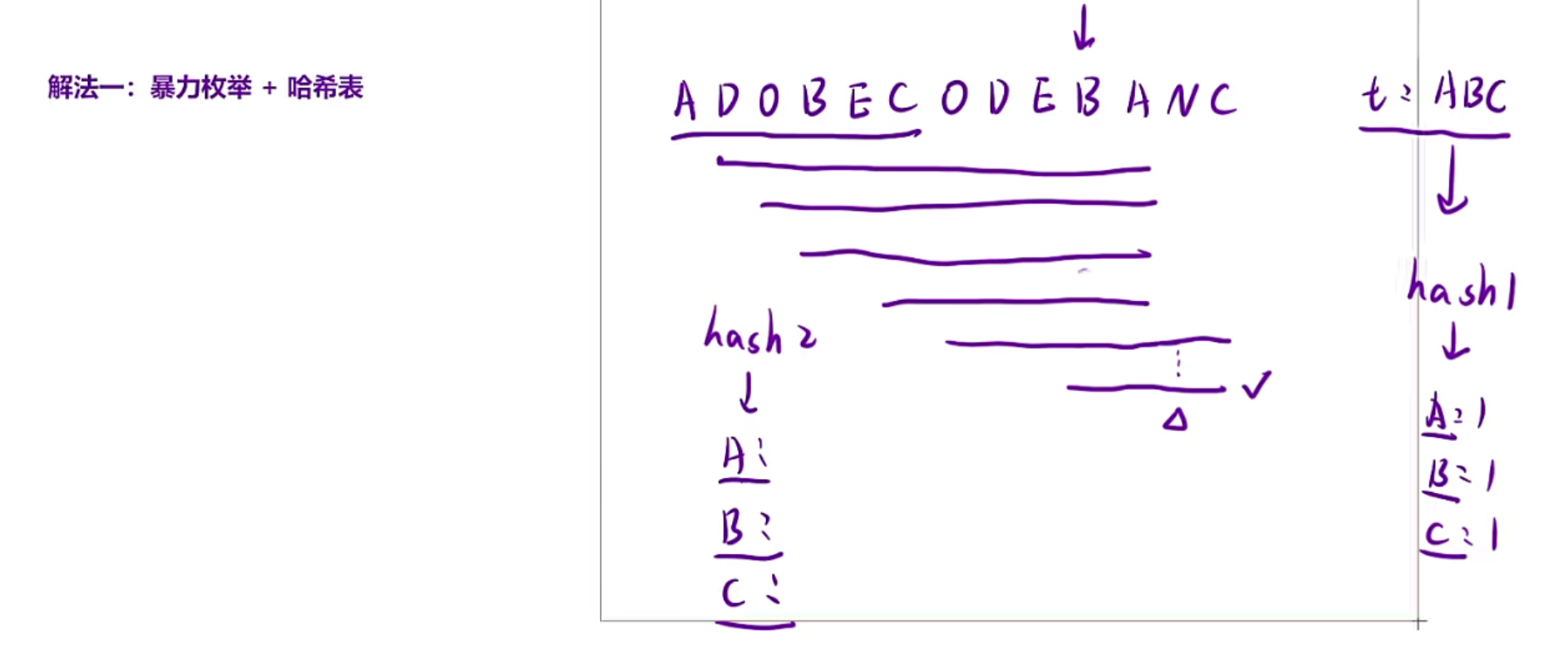
解法二:滑动窗口+哈希表
当我们枚举到一个[left,right]窗口的时候,left++,无非就两种情况,left出窗口时是一个合法的字符,但是hash2当中的每个元素的大小还是>=hash1当中的每个元素的大小,right这是是可以不用动的,如果left是一个非法的字符,那right也是可以不用左移回去的,直接右移寻找下一个合法字符就行,所以这里满足滑动窗口的性质,同向指针+right>left
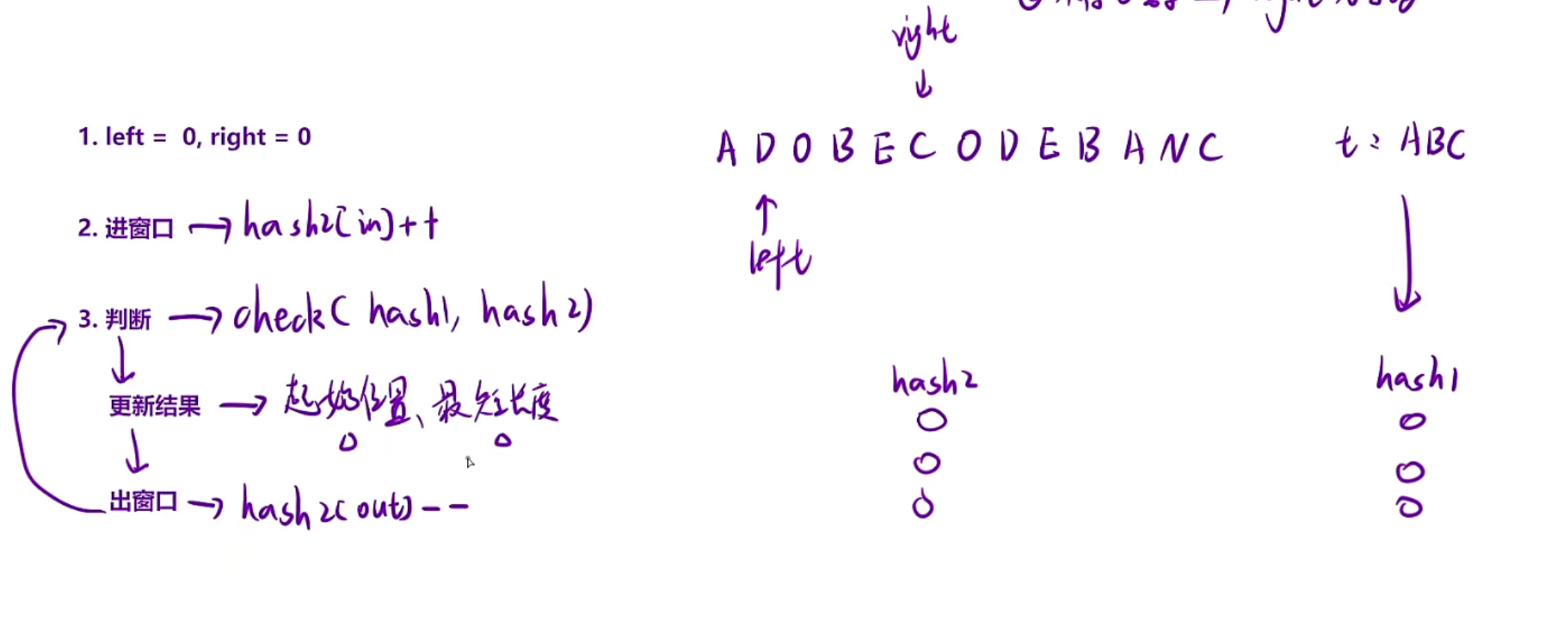

这里count标记的是种类不是个数,比如你ABC都是要求1个就行,但是如果你找到的是两b1a,这样有3个导致判断合法,应该是abc至少各有1个,多的话也是符合
什么叫有效的能够导致count++的,比如你的A要求3个,但是此时你是2个,count就不能++,只有你有的个数>=要求的个数的时候,count才能++,当你的A是3个4个5个的时候,只用统计一次表明是种类就行
当你进窗口的时候,如果个数相等才需要将count++,如果是>就++的话就会导致有很多种类
出窗口的时候,也是只有相等才需要将count--,如果>也--的话就会导致原本是由这种的,但是减掉了
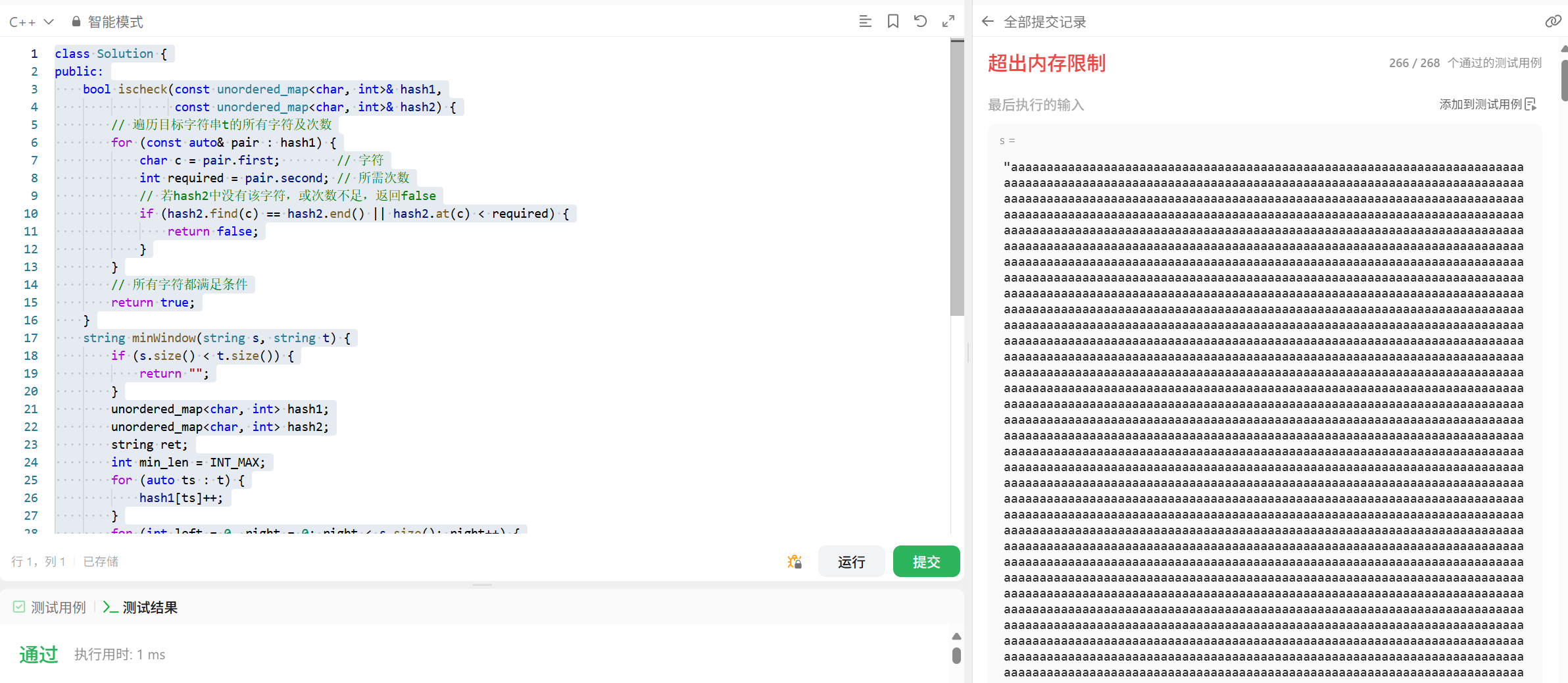
当我每一遍都使用循环去检查两个hash的时候就会超时,所以我们可以使用优化的方法,也就是维护一个count计数器
class Solution {
public:
string minWindow(string s, string t) {
int hash1[128] = {0};
int hash2[128] = {0};
int kind = 0;
for (auto e : t) {
if (hash1[e] == 0)
kind++;
hash1[e]++;
}
int count = 0;
int begin = -1; // 记录合法字符串的起始位置
int min_len = INT_MAX;
for (int left = 0, right = 0; right < s.size();) {
// 进窗口+维护count计数器
hash2[s[right]]++;
if (hash2[s[right]] == hash1[s[right]]) {
count++;
}
// 判断
while (count == kind) {
if ( right - left + 1<min_len) {
begin = left;
min_len = right - left + 1;
}
if (hash2[s[left]] == hash1[s[left]]) {
count--;
}
hash2[s[left]]--;
left++;
}
right++;
}
if(begin==-1)
return "";
return s.substr(begin, min_len);
}
};
总结:
对于滑动窗口,我们需要先想到暴力枚举,如果在暴力枚举中发现,left和right是同向指针,并且right一直在left前面,然后窗口之内能够维护一个动态的符合题意的规定,就能够记录下来
注意:有时候如果题目当中能够有数组代替hash的话就用,这样比较高效,而且有时候能够维护一个count计数器来降低时间复杂度(因为每次对比hash我们都要循环一次,所以维护count的话就不需要)
滑动窗口是一种常用的算法技巧,主要用于解决数组或字符串的子串、子数组相关问题,核心思想是通过维护一个动态的区间(窗口),在这个区间内进行操作,从而将原本需要嵌套循环(时间复杂度较高,如 O(n2))的问题优化到线性时间复杂度(O(n))。
核心概念
- 窗口的定义:通常是数组或字符串中一个左闭右开(或闭区间)的区间,用两个指针(如
left和right)来表示窗口的左右边界。 - 窗口的滑动:通过移动左右指针来 “滑动” 窗口,分为扩张和收缩两个阶段:
- 扩张:右指针向右移动,扩大窗口范围,将新元素纳入窗口,直到满足某个条件。
- 收缩:左指针向右移动,缩小窗口范围,直到不满足条件,在此过程中寻找最优解(如最短、最长子串 / 子数组)。
适用场景
滑动窗口适用于需要连续子串 / 子数组,且满足 “当窗口包含某些特征时,其内部子窗口也可能满足特征” 的问题,典型场景包括:
- 找包含目标字符串所有字符的最短子串(如 “最小覆盖子串” 问题)。
- 找无重复字符的最长子串。
- 找和为目标值的连续子数组。
算法步骤(通用模板)
- 初始化窗口:左指针
left初始化为 0,右指针right从 0 开始移动。 - 扩张窗口:右指针向右移动,将元素加入窗口,同时更新窗口内的统计信息(如字符计数、和等)。
- 满足条件时收缩:当窗口满足题目要求的条件(如包含所有目标字符、和为目标值等),尝试移动左指针缩小窗口,在此过程中更新最优解(如最短长度、最长长度等)。
- 更新统计信息:左指针移动时,同步更新窗口内的统计信息,确保后续判断的正确性。
优势
- 时间复杂度优化:将嵌套循环的 O(n2) 优化为 O(n),因为每个元素最多被左右指针各访问一次。
- 空间复杂度低:通常只需额外的常数空间(如数组、哈希表统计窗口内的信息)。





















 3516
3516

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








