专题六：记忆化搜索（递归优化的秘密武器）

以一个简单题带大家引入记忆化搜索

 

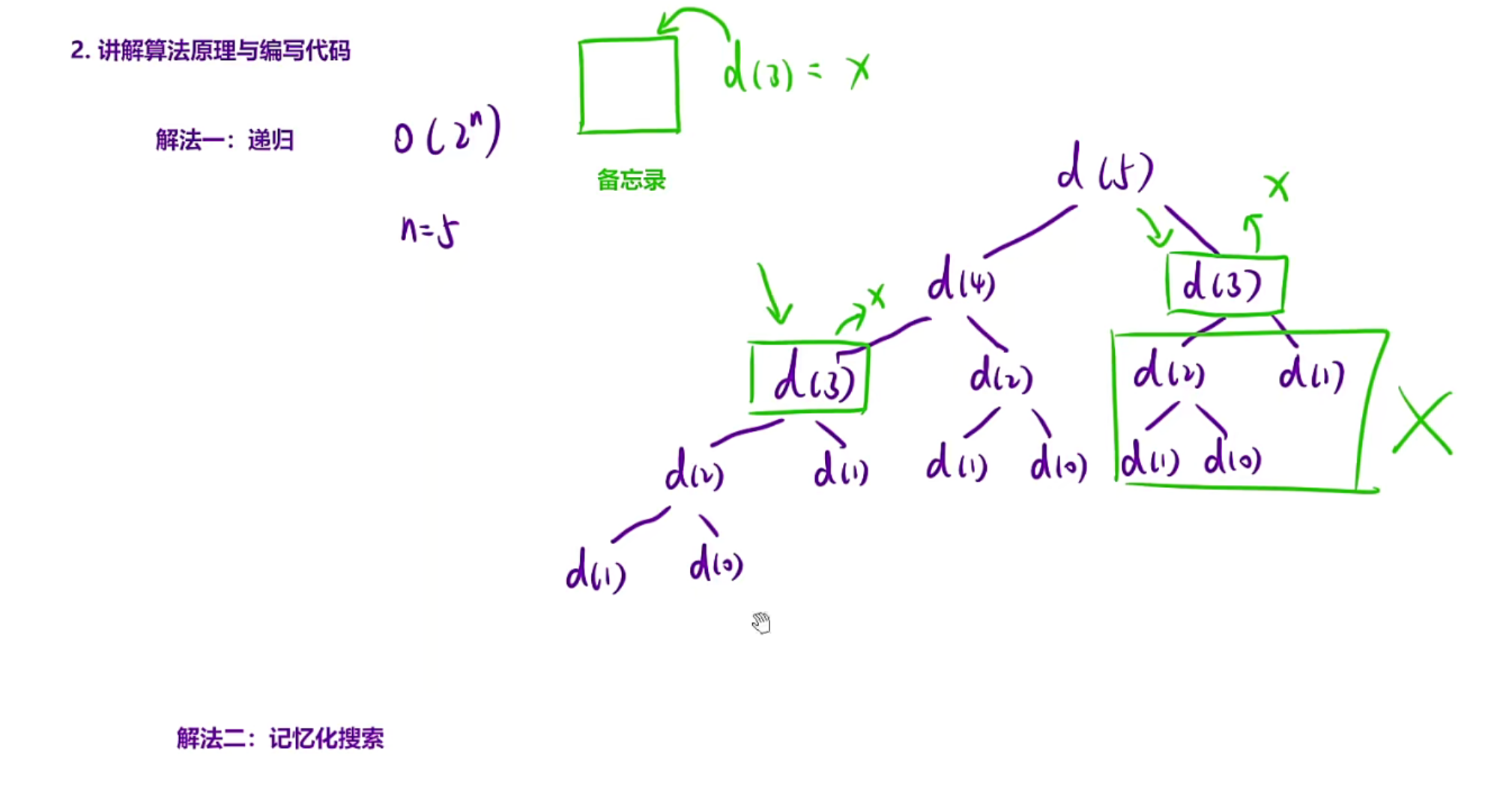
首先我们要先理解递归的解法：

也就是右边那个递归展开图，不难发现递归时间复杂度很大O（2^N）

我们发现d(3)的展开左边和右边是一样的，此时是不是可以想方法当左边递归下去返回d(3)时

把d（3）的结果记住，也就是充当备忘录的身份（这个备忘录可以是一个数组/哈希表等）

记住了当右边递归下去时，发现需要用d(3)，而备忘录当中又有d（3），就不用在展开，直接用

时间复杂度就会减小，这种方法就叫记忆化搜索，（带备忘录的递归）。

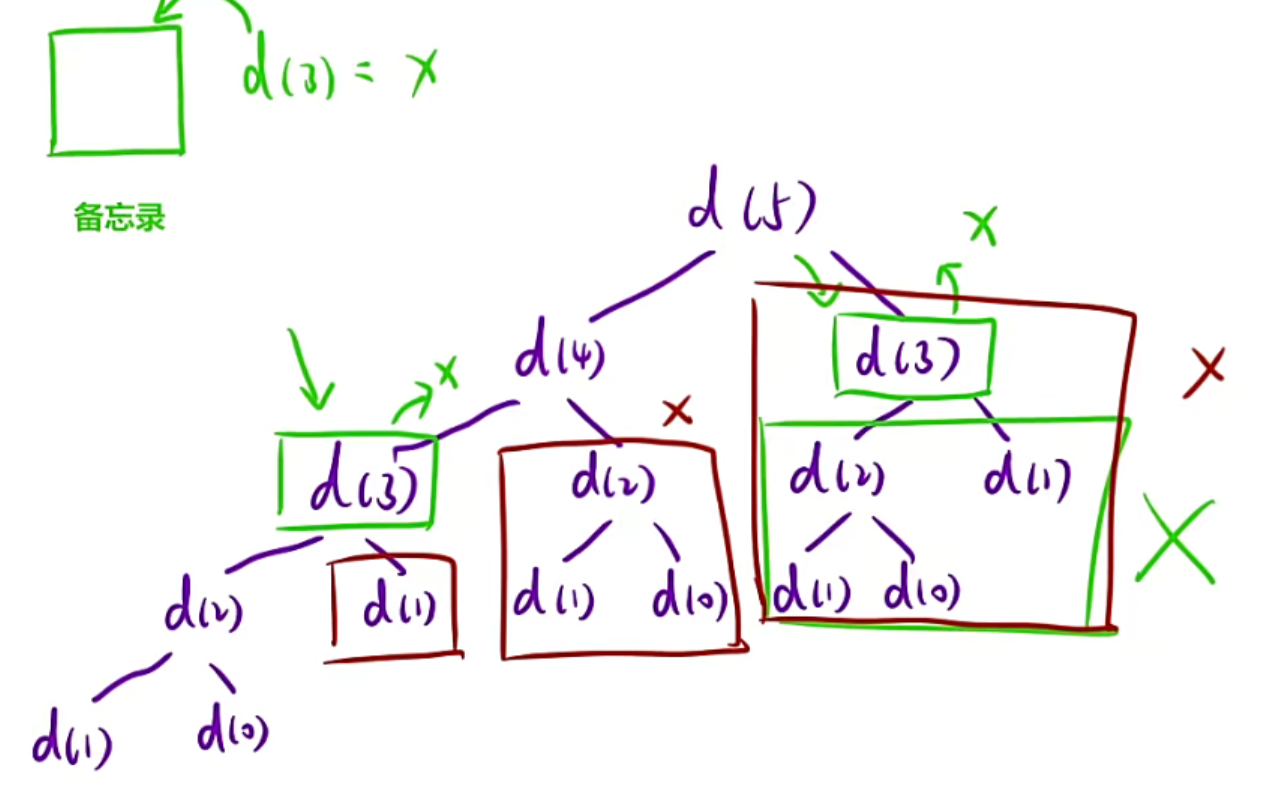
递归左边时，把1~3都记住，会发现很多分支都不会在进去了，画红线的就不会在进去

所以时间复杂度直接变为O（N）

如何实现记忆化搜索？？？

 

添加备忘录时注意找   <可变参数，返回值>  

在这道题就是第几个斐波那契数，它的值是多少，那映射关系就是<int   ,   int >

可以用哈希存，当让也可以用数组，数组下标就对应第几个斐波那契数 

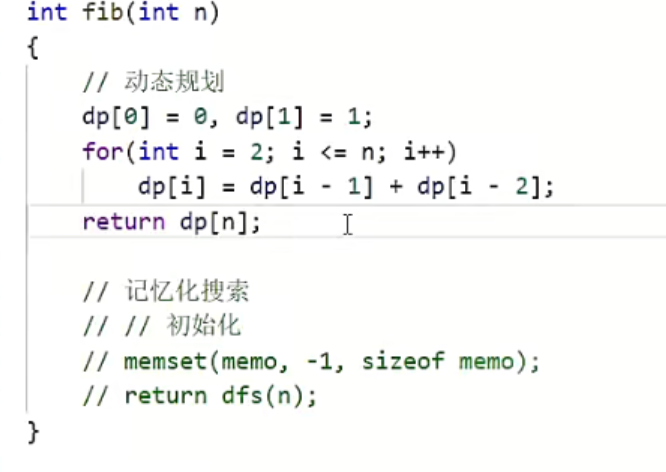
代码编写：

 记忆化搜索与动态规划的梦幻联动

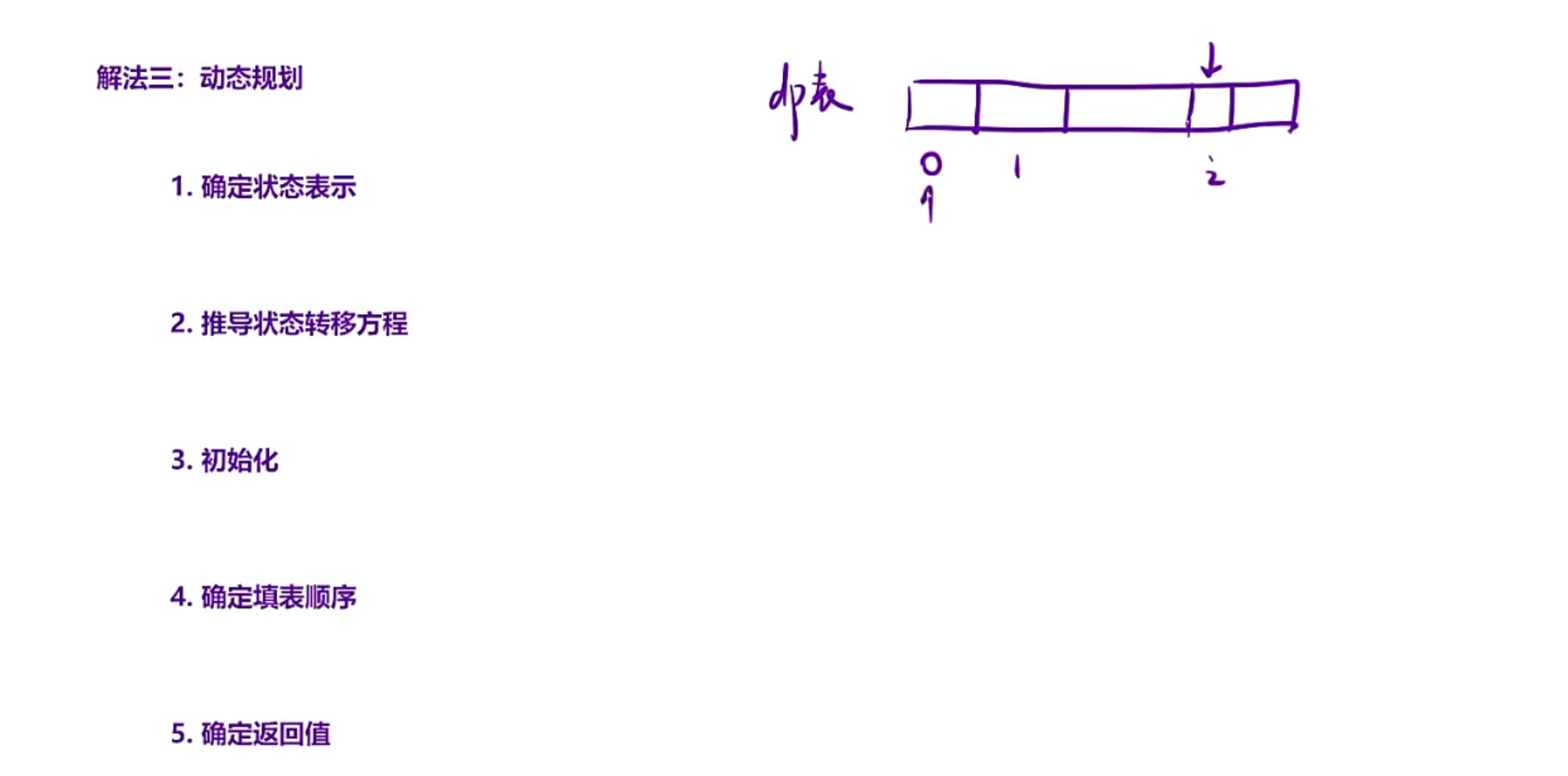
回顾动态规划的解法过程

1.状态表示，就是dp[i]:这个位置表示啥

2.根据状态表示推导状态转移方程，也就是dp[i]=什么

3.初始化：确保填某个位置的时候不要越界

4.填表顺序：填某个位置时需要用到哪些位置，需要填完那些位置才能填这个位置

5.返回值：是返回dp表最大的还是返回dp[i] 

 

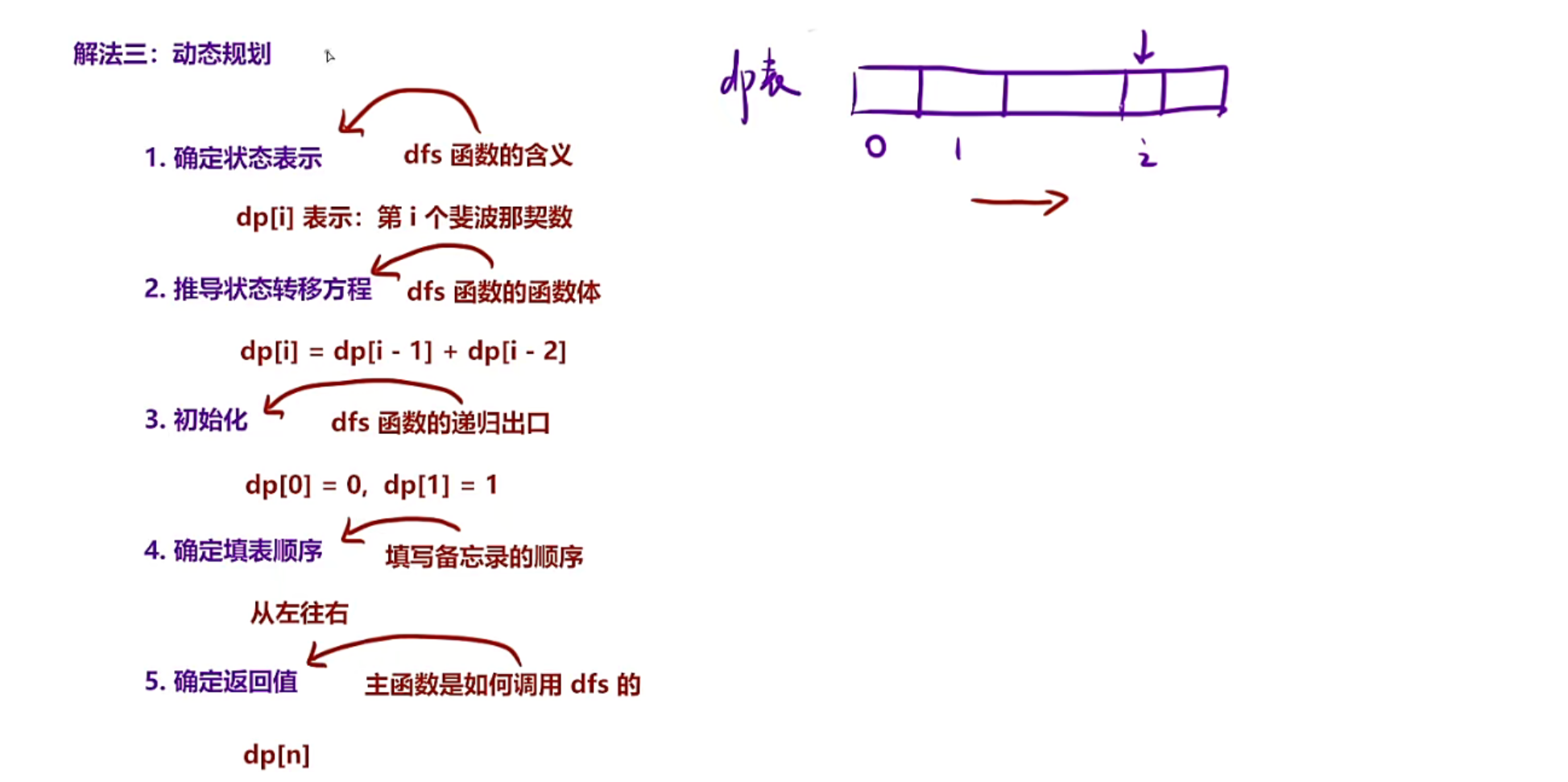
通过上述这道题

1.dfs函数的含义：给第几个斐波那契数列就返回它对应的数值

那你的dp的状态表示不就是dp[i]:第i个斐波那契数列对应的值吗

2.状态转移方程就是dfs函数体，可以看到我们dfs函数体，dfs(n)=dfs(n-1)+dfs(n-2)

3.初始化就是递归出口

4.填表顺序对应的是填写备忘录的顺序，观察递归展开图可以发现，我们是先递归下去

拿到d(0),然后把d(0)放入备忘录，在向上那d(1),放d(1)进入备忘录，依次放

5.返回值，dfs(n),调dfs函数时希望返回第n个，那dp也是返回第n个

可以发现这些都是一一对应的

为什么两个如此相像

 

第一点：它们都是暴力解法（爆搜）

第二点：就是对爆搜的一种优化

第三点：区别：一个是递归的形式，一个是递推的形式 

深入思考问题

1.所有的递归都能改成记忆化搜索吗？？？

显然不是，改成的条件，出现了大量相同的问题时才能用记忆化搜索优化

比如上图的递归展开图，我在求左边d(3)和右边的d(3)时，两个是一样的

而且大量出现才能显示记忆化的优化作用，如果就出现一个两个这种少数其实没必要

 3.自顶向上就是递归的思考流程，自底向上就是动态规划的思考流程

4.其实我们更需要一种能力，就是可以利用暴搜去想动态规划

动态规划最重要的步骤在于状态表示，而不是什么状态转移方程，只有当状态表示搞出来了，状态转移方程才能写正确，那状态表示我们平时如何想？？？

就是根据经验+题目要求，其实我们这一步在做的就是抽象出一个重复的子问题

有没有发现dfs函数的设计就是盯着重复的子问题，每个子问题都在做什么