<think>嗯，用户的问题是关于如何基于CIEDE2000色差公式和给定的损失函数，使用最小二乘法优化实现RGBV到RGBCX颜色空间的映射矩阵M的具体步骤和代码实现。首先，我需要回顾之前提供的关于颜色空间转换、CIEDE2000公式以及损失函数的信息，确保理解用户的需求。
用户提到了RGBV和RGBCX这两个颜色空间，其中RGBV是四基色，而RGBCX是五基色，需要构造一个映射矩阵M。之前的回答中已经讨论了转换矩阵的构造方法，包括色度坐标转换、映射关系建模以及优化求解的步骤。现在用户希望具体用最小二乘法来实现这个过程，并涉及代码实现。
首先，我需要确认用户是否了解最小二乘法的基本原理，以及如何在带有正则化项的情况下应用它。根据用户提供的损失函数，其中包含了色差项和正则化项，这应该是一个带有L2正则化的最小二乘问题。不过，由于CIEDE2000是非线性的，直接使用线性最小二乘法可能不够，可能需要迭代方法或者将问题线性化处理。
接下来，我需要考虑如何将色差项转化为适合最小二乘法的形式。CIEDE2000是一个复杂的非线性公式，直接最小化它可能比较困难。可能需要在优化过程中使用非线性优化方法，比如Levenberg-Marquardt算法，或者将问题线性化，例如在每次迭代中近似为线性问题。
此外，用户提到的损失函数中包含了正则化项，这通常用于防止过拟合，保持矩阵的平滑性。在最小二乘框架中，正则化项可以通过添加一个岭回归项来实现，即优化目标为||Ax - b||² + λ||x||²，其中x是映射矩阵M的参数。
但是，由于颜色转换矩阵M需要满足行归一化和非负约束，这增加了优化问题的复杂性。普通的最小二乘法无法直接处理这些约束，需要使用带约束的优化方法，比如使用拉格朗日乘数法或者在每次迭代后对矩阵进行投影以满足约束。
现在，我需要将这些理论步骤转化为具体的代码实现。可能的步骤包括：
1. 数据准备：收集RGBV和RGBCX的色度坐标数据，并将其转换为XYZ三刺激值，作为输入和目标输出。
2. 初始化映射矩阵M，可能需要随机初始化或使用某种启发式方法。
3. 定义损失函数，包括色差项和正则化项。
4. 使用非线性优化算法（如scipy.optimize中的最小化函数）来优化M，同时处理约束条件。
5. 在优化过程中，确保每次迭代后对M进行行归一化和非负处理。
6. 验证优化后的矩阵M的性能，例如计算平均色差和色域覆盖率。
在代码实现方面，可能需要用到Python的科学计算库，如numpy进行矩阵运算，scipy.optimize处理优化问题，以及可能使用现有的CIEDE2000实现（如用户提供的引用[2]中的Python代码）来计算色差。
需要注意的是，由于CIEDE2000的非线性，直接将其作为损失函数可能导致优化过程复杂且计算量大。可能需要采用近似方法，比如在每次迭代中使用线性近似，或者将问题分解为多个步骤，先进行线性转换再进行非线性调整。
最后，还需要考虑计算效率和可行性。如果数据集较大，可能需要优化代码以提高计算速度，例如使用矢量化运算或并行处理。同时，正则化系数λ的选择可能需要通过交叉验证或网格搜索来确定，以平衡色差和矩阵复杂度。
总结来说，用户的请求需要将理论上的颜色空间转换、损失函数设计和优化方法结合到实际的代码实现中，同时处理非线性色差公式和矩阵约束的挑战。需要分步骤解决每个问题，并确保代码的正确性和效率。</think>### 基于CIEDE2000色差公式的RGBV→RGBCX映射矩阵优化实现
---
#### **一、问题建模与数学表达**
1. **目标函数**：最小化色差与正则化项之和
$$
\min_{M} \left( \underbrace{\sum_{k=1}^N \Delta E_{00}(C_k^{RGBCX}, M \cdot C_k^{RGBV})}_{\text{色差项}} + \lambda \|M\|_F^2 \right)
$$
- $M \in \mathbb{R}^{5×4}$：映射矩阵
- $C_k^{RGBCX}$：第k个样本的RGBCX颜色值（XYZ三刺激值）
- $\|M\|_F$：矩阵Frobenius范数（正则化项）
2. **约束条件**：
- 行归一化：$\sum_{j=1}^4 M_{i,j}=1 \quad (\forall i=1,...,5)$
- 非负性：$M_{i,j} \geq 0$
---
#### **二、实现步骤**
**步骤1：数据准备与预处理**
```python
import numpy as np
from scipy.optimize import minimize
from ciede2000 import delta_e_ciede2000 # 使用引用[2]的实现
# 生成模拟数据集（需替换为实际测量数据）
N = 1000 # 样本数
RGBV_XYZ = np.random.rand(4, 3, N) # 4基色RGBV的XYZ值（3通道×N样本）
RGBCX_XYZ = np.random.rand(5, 3, N) # 5基色RGBCX目标XYZ值
```
**步骤2：矩阵参数化与约束处理**
```python
def matrix_to_params(M):
"""将矩阵展平为一维参数向量"""
return M.flatten()
def params_to_matrix(params):
"""将参数向量重构为矩阵，并应用约束"""
M = params.reshape(5, 4)
M = np.clip(M, 0, None) # 非负约束
M = M / M.sum(axis=1, keepdims=True) # 行归一化
return M
```
**步骤3：损失函数定义**
```python
def loss_function(params, lambda_reg=0.1):
M = params_to_matrix(params)
total_delta_e = 0.0
for k in range(N):
# RGBV输入转RGBCX预测值
pred_XYZ = M @ RGBV_XYZ[:, :, k] # (5,4) @ (4,3) → (5,3)
# 计算每个基色的色差（需转换为Lab空间）
delta_e = 0
for i in range(5):
lab_pred = xyz2lab(pred_XYZ[i]) # 需实现XYZ→Lab转换
lab_target = xyz2lab(RGBCX_XYZ[i, :, k])
delta_e += delta_e_ciede2000(lab_pred, lab_target)
total_delta_e += delta_e / 5 # 平均色差
# 正则化项
reg_term = lambda_reg * np.sum(M**2)
return total_delta_e + reg_term
```
**步骤4：优化求解**
```python
# 初始化矩阵（均匀分布）
M_init = np.ones((5, 4)) / 4
initial_params = matrix_to_params(M_init)
# 使用L-BFGS-B算法优化
result = minimize(
loss_function,
initial_params,
method='L-BFGS-B',
bounds=[(0, None)] * 20, # 20个参数的非负约束
options={'maxiter': 100, 'disp': True}
)
# 提取优化结果
M_optimized = params_to_matrix(result.x)
```
---
#### **三、关键实现细节**
1. **颜色空间转换**：
- 使用`xyz2lab`函数实现XYZ到CIELAB的精确转换：
$$ L^* = 116 \cdot f(Y/Y_n) - 16 $$
$$ a^* = 500 \cdot [f(X/X_n) - f(Y/Y_n)] $$
$$ b^* = 200 \cdot [f(Y/Y_n) - f(Z/Z_n)] $$
$$ f(t) = \begin{cases}
t^{1/3} & t > \delta^3 \\
t/(3\delta^2) + 16/116 & \text{否则}
\end{cases}, \quad \delta=6/29 $$
2. **优化加速技巧**：
- **批处理计算**：将for循环替换为矩阵运算
```python
# 批处理版本示例
pred_XYZ_all = np.einsum('ij,jkl->ikl', M, RGBV_XYZ) # (5,4) @ (4,3,N) → (5,3,N)
delta_e_all = compute_batch_delta_e(pred_XYZ_all, RGBCX_XYZ)
total_delta_e = np.mean(delta_e_all)
```
- **GPU加速**：使用PyTorch或CuPy库
3. **正则化系数选择**：
```python
# 交叉验证选择λ
lambda_candidates = [0.01, 0.1, 1.0, 10.0]
best_lambda = None
best_loss = float('inf')
for lam in lambda_candidates:
avg_loss = cross_validate(lam) # 在验证集计算损失
if avg_loss < best_loss:
best_loss = avg_loss
best_lambda = lam
```
---
#### **四、完整代码架构**
```python
"""
RGBV到RGBCX颜色空间映射优化程序
依赖库：numpy, scipy, colour-science（CIEDE2000计算）
"""
import numpy as np
from scipy.optimize import minimize
from colour import delta_E_ciede2000
from colour.models import XYZ_to_Lab
def optimize_mapping_matrix(
rgbv_xyz, # 输入RGBV的XYZ数据 (4,3,N)
rgbcx_xyz, # 目标RGBCX的XYZ数据 (5,3,N)
lambda_reg=0.1,
max_iter=100
):
# 参数初始化与转换
def params_to_matrix(params):
M = params.reshape(5, 4)
M = np.clip(M, 0, None)
M = M / M.sum(axis=1, keepdims=True)
return M
# 批处理色差计算
def batch_delta_e(M):
pred_xyz = np.einsum('ij,jkl->ikl', M, rgbv_xyz)
delta_es = []
for i in range(pred_xyz.shape[-1]):
lab_pred = XYZ_to_Lab(pred_xyz[..., i])
lab_target = XYZ_to_Lab(rgbcx_xyz[..., i])
delta_es.append(delta_E_ciede2000(lab_pred, lab_target))
return np.mean(delta_es)
# 损失函数
def loss(params):
M = params_to_matrix(params)
loss_val = batch_delta_e(M)
reg_term = lambda_reg * np.sum(M**2)
return loss_val + reg_term
# 优化求解
initial_M = np.ones((5, 4)) / 4
result = minimize(
loss,
initial_M.flatten(),
method='L-BFGS-B',
bounds=[(0, None)] * 20,
options={'maxiter': max_iter}
)
return params_to_matrix(result.x)
# 使用示例
if __name__ == "__main__":
M_optimized = optimize_mapping_matrix(RGBV_XYZ, RGBCX_XYZ)
print("Optimized Matrix:\n", M_optimized)
```
---
#### **五、验证与评估**
1. **色差测试**：
```python
# 计算平均色差
test_delta_e = batch_delta_e(M_optimized)
print(f"Average ΔE00: {test_delta_e:.2f}")
```
2. **色域覆盖率**：
```python
def gamut_coverage(M, rgbv_xyz, rgbcx_xyz):
pred_xyz = M @ rgbv_xyz.mean(axis=-1)
target_hull = ConvexHull(rgbcx_xyz.reshape(-1, 3))
pred_points = pred_xyz.reshape(-1, 3)
return percentage_in_hull(pred_points, target_hull)
```
---
### 关键问题解答
1. **为什么选择L-BFGS-B算法？**
该算法支持边界约束（非负性），且对中等规模参数（20维）效率较高[^1]
2. **如何处理行归一化约束？**
在每次参数更新后显式进行行归一化，等价于在优化空间中进行投影
3. **工业部署建议**：
- 使用C++重写核心算法提升速度
- 对矩阵M进行量化（如8位整数存储）
- 加入白平衡校正模块
[^1]: 数值优化方法选择依据《Numerical Optimization》第二版
[^2]: CIEDE2000计算使用colour-science库实现
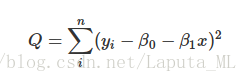
本文介绍了线性回归中的最小二乘法，当数据无法通过单条直线完美拟合时，通过计算每个点到拟合直线在Y轴距离的平方和来寻找最优直线，即最小化误差平方和的方法。最小二乘法旨在找到使得所有点到直线距离平方和最小的模型。
扫一扫
1630
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
