期望、均值、拟合

均值和期望的差别：

1、均值是对已经观测到的数据的计算，例如已经掷骰子6次，2，2，2，4，4，4，那么计算他的均值就是(2+2+2+4+4+4)/6=3；而数学期望是对未来数据（或者叫还未观测到的数据，或者叫还未带入模型计算的数据）的计算。例如假设还要掷骰子100次，那么这100次投掷骰子的均值就是期望，如何计算呢？因为已知每投掷骰子一次，每个数字出现的概率是1/6，那么投掷骰子100次每个数字出现的概率就是100*(1/6)，那么最终的期望就是

( 1×(100*(1/6)) + 2×(100*(1/6)) + 3×(100*(1/6)) + 4×(100*(1/6)) + 5×(100*(1/6)) + 6×(100*(1/6)) ) / 100

= 1×(1/6) + 2×(1/6) + 3×(1/6) + 4×(1/6) + 5×(1/6) + 6×(1/6)

= (1 + 2 + 3 +4 + 5 + 6) / 6 = 3.5

如果掷骰子的次数趋近于正无穷，那么均值趋近于数学期望。

1、均值是等权平均，期望是加权平均，而等权平均是加权平均的一个特例。例如上面例子中， 每一个数字出现的概率都是相同的1/6，如果骰子被做了手脚，比如加了铅块使得每个数字出现的概率不同了，1出现的概率为7/24，2出,现的概率是1/6，3出现的概率是1/6，4出现的概率是1/8，5出现的概率是1/8，6出现的概率是1/8。（无论概率如何变化，6个数字概率相加必然是1），那么掷骰子N次的数学期望是：

1×(7/24) + 2×(1/6) + 3×(1/6) + 4×(1/8) + 5×(1/8) + 6×(1/8) = 3

3和每个数字出现概率都是1/6的期望3.5不相同了。

一、均值

均值，其实是针对实验观察到的特征样本而言的。比如我们实验结果得出了x1,x2,x3…..xn这n个值，那么我们的均值计算是

比如我们进行掷骰子，掷了六次，点数分别为2，2，2，4，4，4，这六次的观察就是我们的样本，于是我们可以说均值为(2+2+2+4+4+4)/6=3。但是千万不能说期望是3，说概率是3就明显的弄混了均值和期望的概念，下面解释一下期望的概念。

二、期望

期望是针对于随机变量而言的一个量，可以理解是一种站在“上帝视角”的值。针对于他的样本空间而言的。

均值是一个统计量(对观察样本的统计)，期望是一种概率论概念，是一个数学特征。

首先给出定义公式

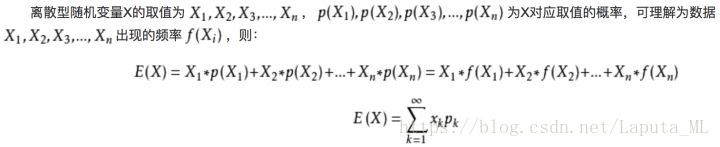
那么上面那个掷骰子例子对应的期望求法如下：

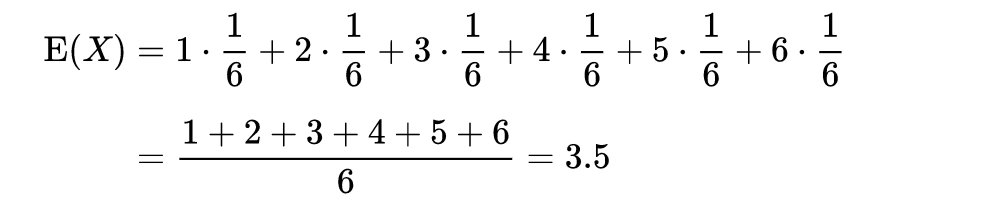
可以看出期望是与概率值联系在一起的，如果说概率是频率随样本趋于无穷的极限 ，期望就是平均数随样本趋于无穷的极限，可以看出均值和期望的联系也是大数定理联系起来的。

三、例子

上面说到期望就是平均数随样本趋于无穷的极限，那么这句话是什么意思呢？

我们还是以上面的掷骰子为例子：

如果我们掷了无数次的骰子，然后将其中的点数进行相加，然后除以他们掷骰子的次数得到均值，这个有无数次样本得出的均值就趋向于期望。类似于下面这样：

四、总结

概率是频率随样本趋于无穷的极限

期望是平均数随样本趋于无穷的极限