C/C++ 链表实现----Harsha Suryanarayana
(来自印度的顶级程序员。一些添加,c++部分为个人理解)
关于Harsha Suryanarayana:
https://www.freecodecamp.org/chinese/news/mycodeschool-youtube-channel-history/
B站视频:
【【强烈推荐】深入浅出数据结构 - 顶尖程序员图文讲解 - UP主翻译校对 (已完结)】https://www.bilibili.com/video/BV1Fv4y1f7T1?vd_source=2cb4b275b46b9a0bd5d3d0e3d51588e6
油管:https://www.youtube.com/watch?v=92S4zgXN17o&list=PL2_aWCzGMAwI3W_JlcBbtYTwiQSsOTa6P
仓库:
GitHub:https://github.com/LIangZH-RT/data_structure_code
gitee:https://gitcode.com/LangZH_RT/data_structure_code/tree/main
链表-节点
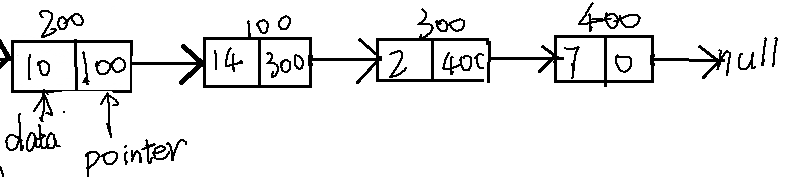
链表由多个节点组成,每一个节点有两个部分,指针和数据。指针用于存储下一个节点的地址(可认为就是下一个节点,只不过是指针形式),建立连接;数据部分用于存储数据。此外,链表中可有一个的头节点,该头节点与普通节点结构相同,但是没有数据内容,它会连接第一个实际的数据节点。
一个链表的结构(无头节点):
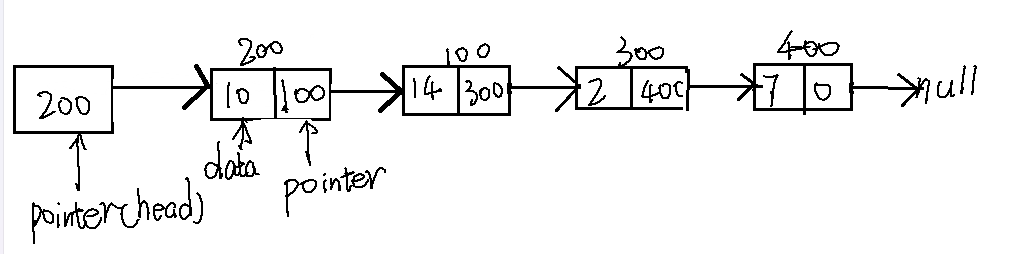
由它的结构来看,应用结构体或者类来实现一个节点。
//c
typedef struct Node {
int data; //节点中的数据部分 int为对应的数据类型
struct Node * next; // 节点中的指针部分 你可以读为它的下一节点
}Node;
//c++ 与c类似
class Node {
pubilc:
int data;
Node* next;
};
链表的操作
(1)创建节点
创建节点可以写为一个函数,简便之后出现创建节点部分的代码。
Node* createNode(int data) {
Node* temp = (Node*)malloc(sizeof(Node));
//可以在此处添加内存申请失败的处理
temp->data = data;
temp->next = NULL;
return temp;
}
c++的代码使用类和模板,可以实现与stl中的list用法类似。
//在c++中可以用另一个类把链表的操作封装一起
template<typename T>
class Node {
public:
T data;
Node* next;
};
template<typename T>
class LinkedList {
public:
Node<T>* createNode(T data);
};
template<typename T>
Node<T>* LinkedList<T>::createNode(T data) {
Node<T>* temp = new Node<T>;
temp->data = data;
temp->next = nullptr;
return temp;
}
考虑到c++再实现一遍会占用大量篇幅,所以以下会只会用c语言实现,感兴趣可在仓库中查看c++版本。
(2)在链表中插入一个节点
将节点连接的操作为:节点1的next = 节点2的地址
在头部插入一个节点
先给出一个头指针,作为访问链表的入口。
Node * head = NULL; 头指针,用于保存第一个节点的地址。(D data P pointer)。关键步骤:修改头指针指向。
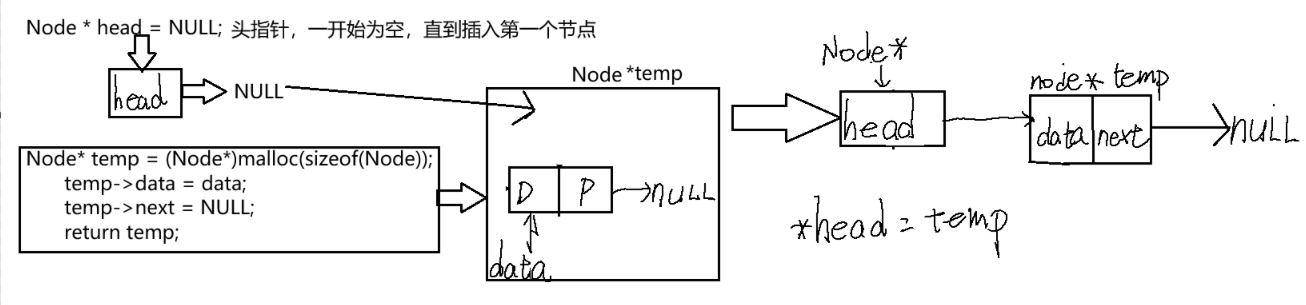
对于图的解释:一开始头指针为空的情况,在堆中得到temp节点(createNode函数)。修改head,用head头指针保存第一个节点,就可以成功将第一个节点加入,你可以再调试中查其中变量值的变化过程,主要是head的值和next的值。
void insertHead(Node ** head,int data){
Node * temp = createNode(data);
if(*head == NULL) *head = temp;
}
插入函数应传入头指针的指针,因为在头部插入需要修改头指针的指向。使用一些数字代表地址,框中数字代表它保存的地址。插入过程(*head = temp)如下所示:
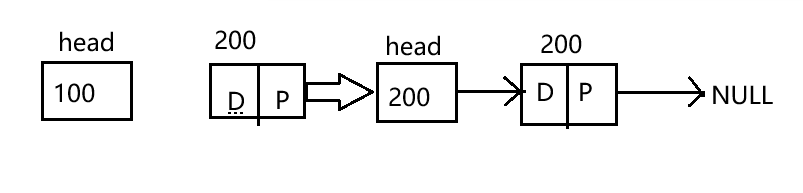
另外还需要考虑linkedlist不是空的情况,即 head != NULL;图示过程,序号代表操作顺序:
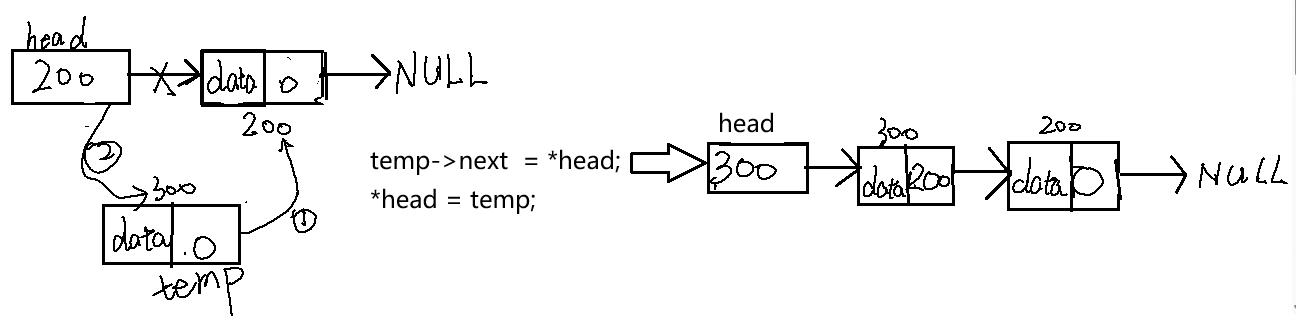
此时需要修改创建出的temp节点的next指针指向和head的指向,必须先修改当前申请的节点的next指向。
如果先修改head会丢失原先head的指向,导致temp的next指向错误。
由于空链表head为NULL,就不需要判断,直接temp->next = *head(因为与创建时将其设为NULL等价,所以不会有影响)。完整的头插入函数:
void insertHead(Node ** head,int data){
Node * temp = createNode(data);
temp->next = *head;
*head = temp;
}
在尾部插入节点
有头节点。此时子需要让最后一个节点的next指针指向要插入的节点即可。
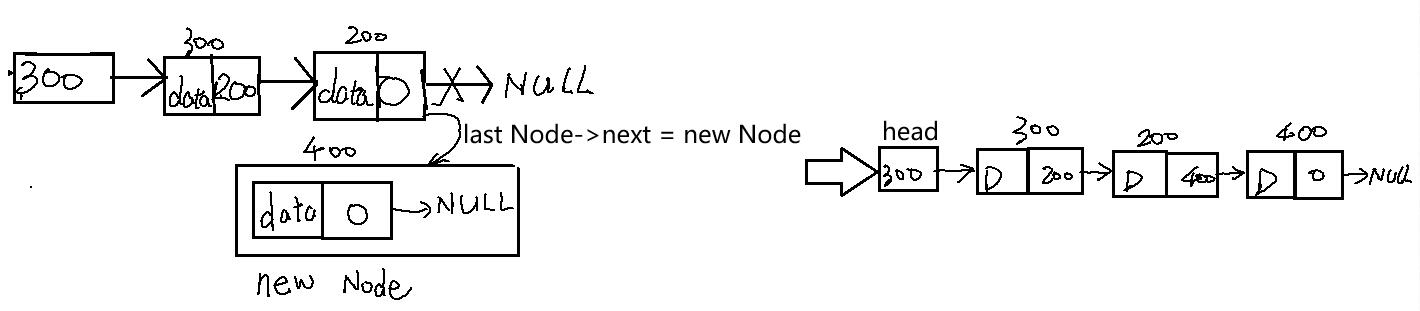
关键步骤:修改最后一个节点的next。利用头指针遍历到最后一个节点,可用循环实现。一直判断当前节点的下一节点是否为空,空就停止,因为最后一个节点的下一节点(next指针)为空,这样就可以正确找到最后一个节点,尾插入函数:
void push_Back(Node * head, int data) {
Node * newNode = createNode(data);
Node * temp = head;
while(temp->next != NULL){
temp = temp->next; //个人解读:当前临时节点 = 当前临时节点的下一节点
}
temp->next = newNode;
}
过程:
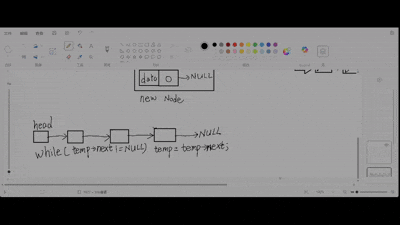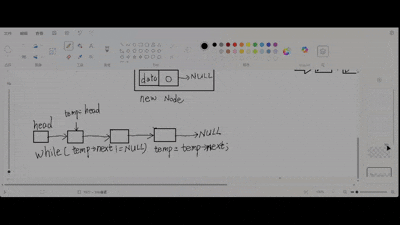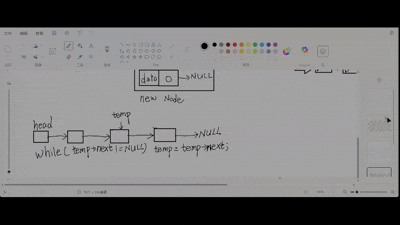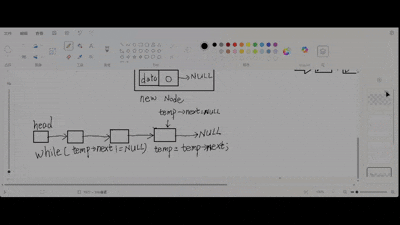
特殊情况:链表为空。按照在头插入节点方式修改代码,传入头指针的指针,在head空时按头插入执行。
void push_Back(Node ** head, int data) {
Node * newNode = createNode(data);
Node * temp = *head;
//添加判断头部情况
if(*head == NULL) {
*head = temp;
return;
}
while(temp->next != NULL){
temp = temp->next;
}
temp->next = newNode;
}
在任意位置插入一个节点
以在3位置插入一个节点为例。图示中已断开节点2和节点3的链接,在中间插入一个节点。需要将插入位置的 前一节点的next指针指向 插入节点,插入节点的next指针指向前一节点的next(前一节点的next指向为原先的下一个节点)。图示清晰展示:
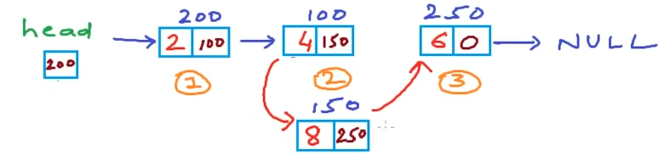
定义一个insert函数,传入参数Node ** head ,int data,返回void,并且创建好新节点。
void insert(Node ** head,int data){
Node * newNode = createNode(data);
}
给定一个临时节点,赋值为头指针,让临时节点循环到插入位置的前一节点。
Node * temp = *head;
for(int i=0;i<pos-2;i++){
temp = temp->next;
}
for中的语句与在插入尾部插入元素一样,执行一次temp就会跳一次,到下一节点。接下来须要建立新连接。此时temp为节点2
//先改变插入的节点的next 如果先改变temp的next会丢失节点3
newNode->next = temp->next;
//将当前节点与原先节点3连接 这样插入节点就占原先节点3的位置
temp->next = newNode;
但是还需要考虑pos = 1会导致pos - 2 < 0。需要添加判断,pos = 1为在位置1插入节点,就是在头部插入节点,按照在头部添加节点方法稍加修改即可。再加入pos的检测和超出链表长度的检测。完整插入函数:
void insert(Node ** head,int data,int pos){
Node * newNode = createNode(data);
if(pos < 1) return;
if(pos == 1) {
newNode->next = *head;
*head = newNode;
return;
}
Node * temp = *head;
for(int i=0; i<pos-2; i++){
//超出链表判断
if(temp->next == NULL) return;
temp = temp->next;
}
newNode->next = temp->next;
temp->next = newNode;
}
(3)删除
删除一个节点
以此处的节点3为例,断开节点2和节点3连接,连接节点2和节点4。需要得到节点2的地址,通过改变节点2的next指向和free节点3,就可以断开连接,实现删除。

步骤1:fix the links
经过上面的任意位置插入节点,你已经知道了如何到达节点2的位置。现在,得有一个变量记录节点2的地址,一个变量保存节点3地址。
Node * temp1 = head;
int i;
//跳到节点2
for(i = 0;i < pos-2;i++){
temp1 = temp1->next;
}
Node * temp2 = temp1->next; //temp2存储节点节点3
//修复连接 节点2的下一节点指向节点3的下一节点(节点4)
temp1->next = temp2->next;
步骤2:free the space
//最后释放节点3
free(temp2);
特殊情况,如插入一样当pos为1时(删除节点1),pos-2<0 。添加判断即可,完整删除函数:
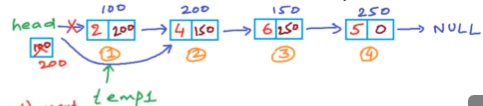
void remove(Node **head,int pos){
Node * temp1 = *head;
//判断pos
if(pos == 1){
*head = temp1->next;
free(temp1);
return;
}
int i;
//找到节点2
for(i = 0;i < pos-2;i++){
temp1 = temp1->next;
}
Node * temp2 = temp1->next; //temp2存储的节点3
//修改链接 节点2的下一节点指向节点3的下一节点(节点4)
temp1->next = temp2->next;
//清除释放节点3
free(temp2);
}
(4)反转一个链表
注意:此处的反转并未限定链表的节点数,当节点数大于2时,才能使用。
循环实现
给定一个链表。

反转后:

就是让原先的节点的next指针指向上一节点,并且重新设置头节点。
从第一个实际节点开始,反转链表时第一个节点将变为最后一个节点,由于节点的上一节点为NULL,所以它的next将赋值为NULL。
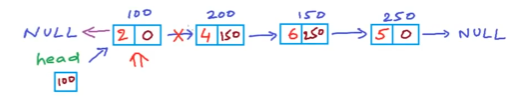
但此时会丢失节点2的地址,所以需要用另一个变量保存节点2的地址。改变节点2:
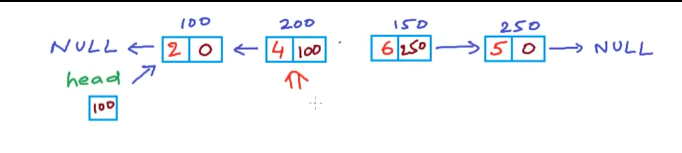
如此类推直到最后一个节点。现在开始吧:
先有3个变量一个为修改中的节点,另两个为这个节点的上一节点和下一节点。为了清晰知道变量含义,给名字为prev(前一个),current(当前),next(下一个)。第一个节点由head存储,前一节点为NULL。先以试着修改第一节点。
Node *prev, *current, *next;
next = current->next;
current = *head;
prev = NULL;
{
current->next = prev;
//修改完之后移动,所有变量代表节点都向后移动一次,移动顺序必须为prev,current,next
prev = current;
current = next;
next = current->next;
}
利用之前提到的循环遍历节点方法实现 { } 中的内容,直至当前节点为空,再修改head的指向。可以修改
next = current->next; 位置少一行代码。完整反转函数:
void reverse(Node **head){
Node *prev, *current, *next;
prev = NULL;current = *head;
while(current != NULL){
next = current->next;
current->next = prev;
prev = current;
current = next;
}
*head = prev;
}
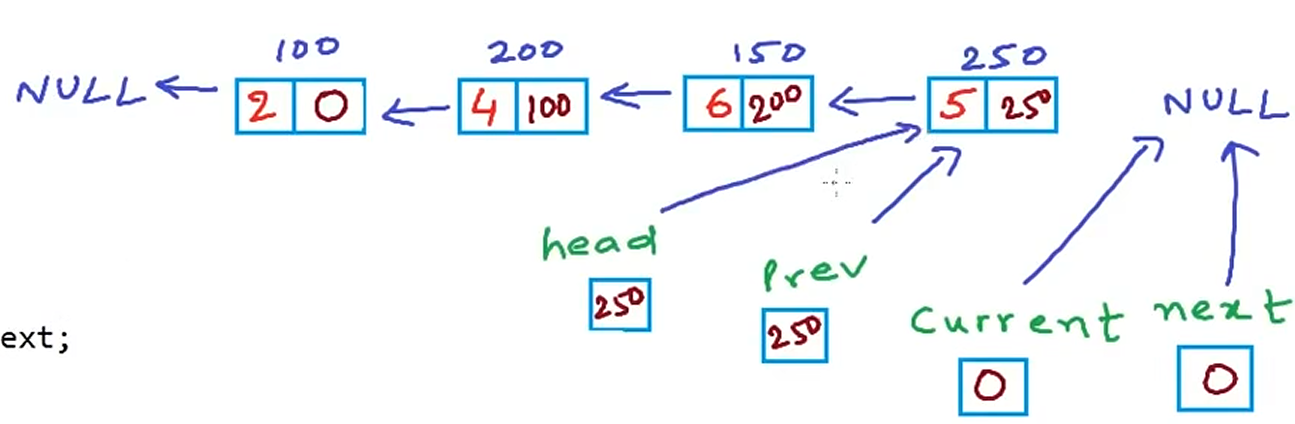
当current移动到最后一个节点时,反转之后,整体会再移动一次,结果就如上图所示.所以循环条件就是current是否空,head也应指向prev。
递归实现
递归实现代码更加简洁,但相对更难理解,必须对递归过程相当了解。递归必须有出口,否则爆栈。对于链表,递归到最后一个节点,判断它的next指针是否空。
if(current->next != NULL){
//到达最后一个节点 修改头并且退出函数
*head = current;
return;
}
由此应传入两个参数当前节点和头,先看看完整反转函数:
void reverse(Node **head ,Node * current){
if(current->next == NULL){
*head = current;
return;
}
reverse(head , current->next);
//反转操作
Node * temp = current->next;
temp->next = current;
current->next = NULL;
}
第二个参数可以传入头指针,它指向第一个实际节点。
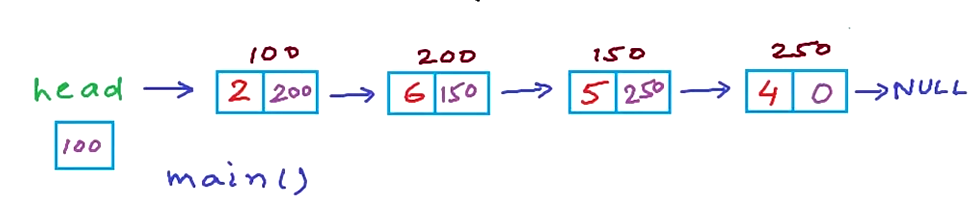
函数实在栈上的所以先执行的会在栈底,当递归到最后一个节点时,根据判断条件reverse会直接出栈。图示递归:
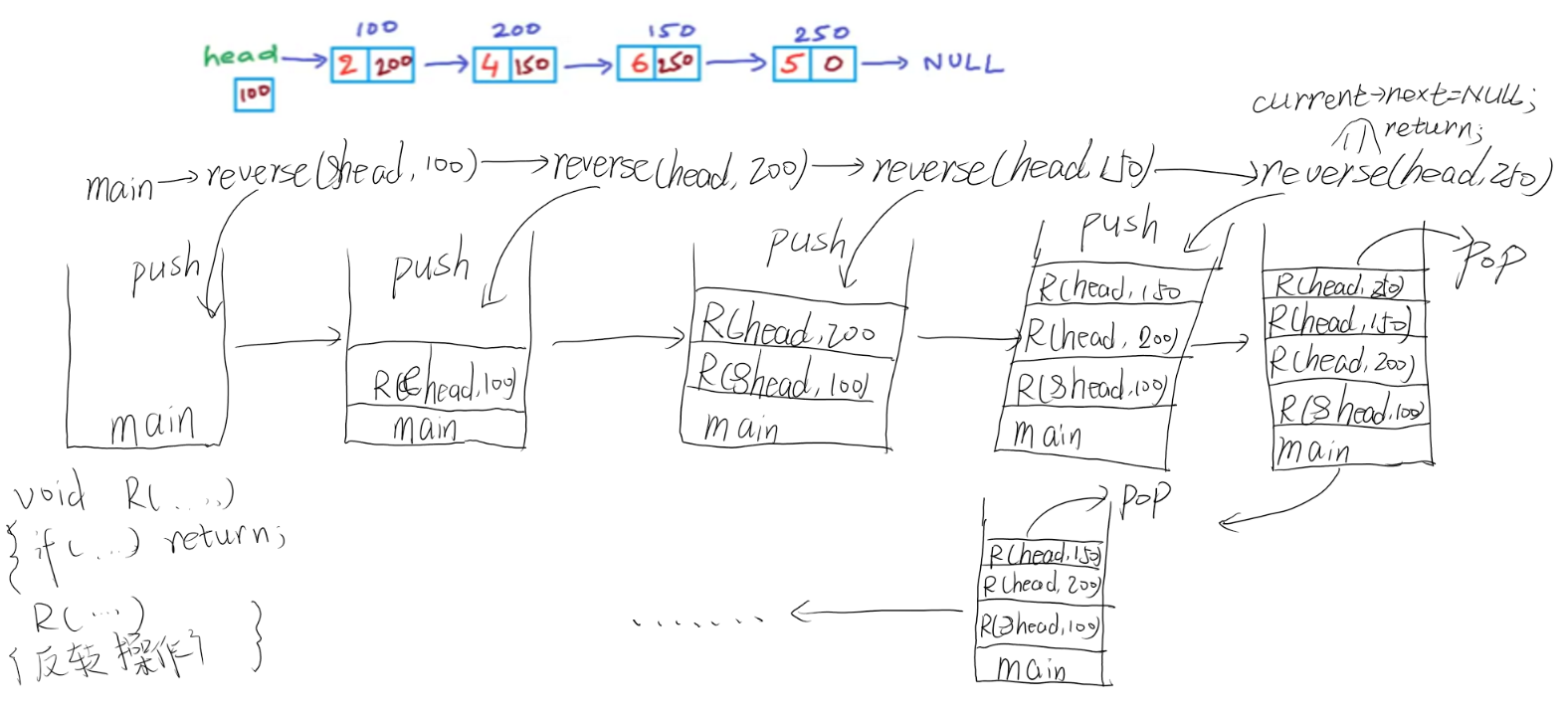
栈顶函数优先出栈,所以函数执行为先R(head, 250) 。此时下一节点为空,if条件成立,调整head。可以把所有的执行过程写出:

由此可以看出递归的过程,如果实在不懂,启动调试,逐语句进行,慢慢看执行过程。
结语
整个链表的基础就到此,后续会出双向链表。感谢Harsha Suryanarayana的视频。
如果有疑问或者文章中有误,欢迎私信,联系邮箱:aa2961363680@outlook.com。
坚持下去你也能成为像他一样的大神。





















 4288
4288

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








