二叉树----12.从前序与中序遍历序列构造二叉树

题目链接

/**

            已知:

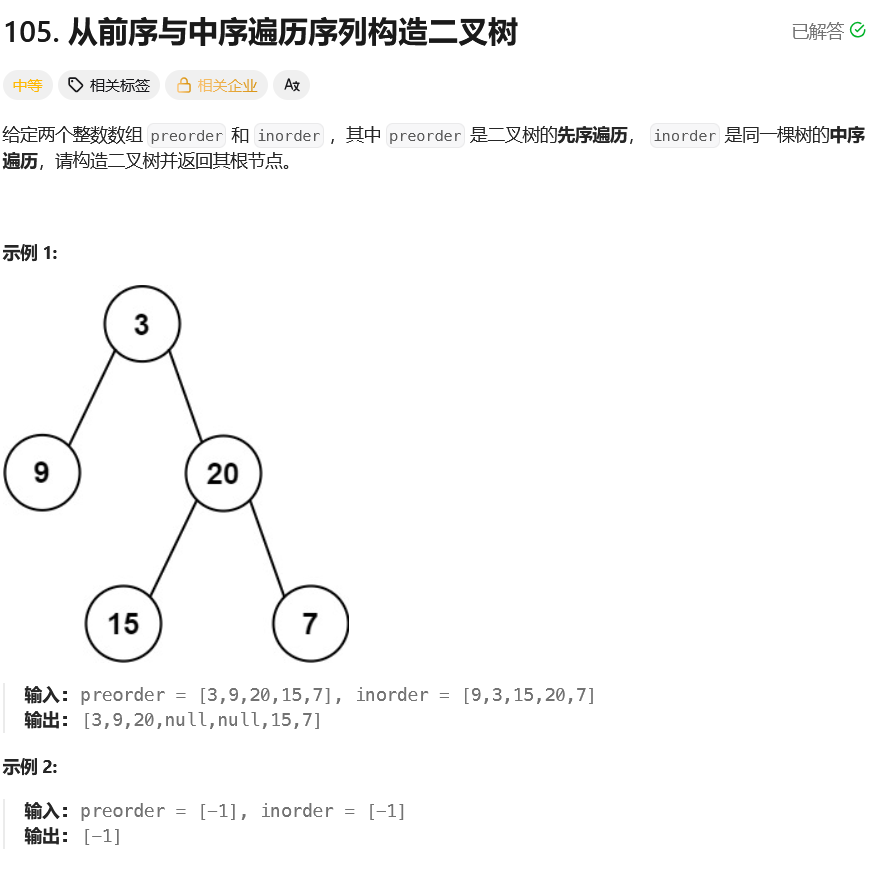
                先序遍历(根 左 右) 与 中序遍历(左 根 右)的顺序 构建二叉树

            解法:

                1.由先序遍历确定根节点(数组第一个元素)  创建节点实例

                2.在中序遍历的数组中找到根节点,根节点两侧的元素即为二叉树的左子树与右子树

                3.被分割的子数组 两侧第一个元素即为子树的根节点 重复上述流程即可

            由遍历序列构建二叉树的通解:

                                    中序序列必备 先序，后序序列任意

                                    由先序(第一个)或后序(最后一个)确定根节点

                                    再从中序序列中定位根节点 两侧即为左右子树的节点

                                    重复上述流程 递归构建即可

*/

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int[] preorder;
    private int[] inorder;
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        /**
            已知:
                先序遍历(根 左 右) 与 中序遍历(左 根 右)的顺序 构建二叉树
            解法: 
                1.由先序遍历确定根节点(数组第一个元素)  创建节点实例
                2.在中序遍历的数组中找到根节点,根节点两侧的元素即为二叉树的左子树与右子树
                3.被分割的子数组 两侧第一个元素即为子树的根节点 重复上述流程即可
            由遍历序列构建二叉树的通解:
                                    中序序列必备 先序，后序序列任意
                                    由先序(第一个)或后序(最后一个)确定根节点
                                    再从中序序列中定位根节点 两侧即为左右子树的节点
                                    重复上述流程 递归构建即可
        */
        this.preorder = preorder;
        this.inorder = inorder;
        return buildTree(0, preorder.length - 1, 0, inorder.length - 1);
    }


    private TreeNode buildTree(int preStart, int preEnd, int inStart, int inEnd) {
        if(preStart > preEnd || inStart > inEnd) { //任意一个数组为空 都代表构建完毕
            return null; 
        }

        //先序数组的第一个元素 即为根节点
        TreeNode root = new TreeNode(preorder[preStart]);

        //找到根节点在中序数组中的位置 区分左子树与右子树
        int index = -1;
        for(int i = inStart; i <= inEnd; i++) {
            if(inorder[i] == preorder[preStart]) {
                index = i;
                break;
            }
        }

        //计算左子树的节点个数
        //用于重新划定左 右子树 的先序数组
        int count = index - inStart;

        //递归构建左子树与右子树
        root.left = buildTree(preStart + 1, preStart + count, inStart, index - 1);
        root.right = buildTree(preStart + 1 + count, preEnd, index + 1, inEnd);

        return root;
    }
}