二叉树----11.二叉树展开为链表

题目链接

/**

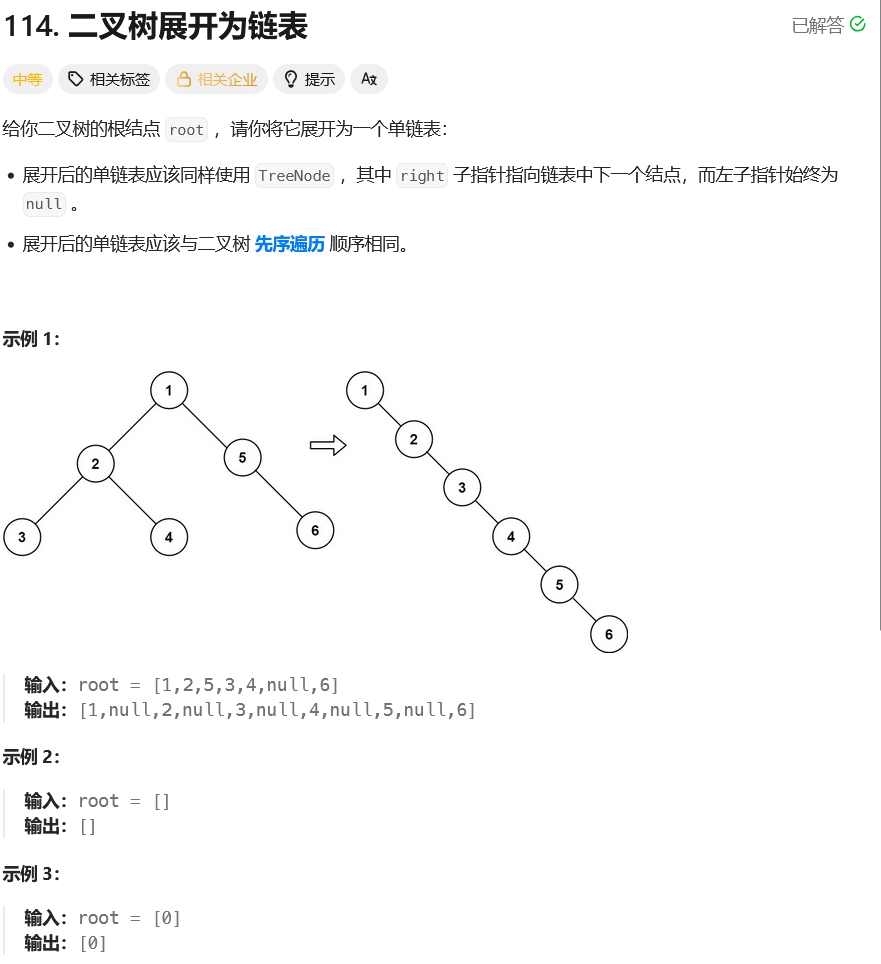
            展开后的链表与二叉树的先序遍历顺序相同

            即 链表顺序为 根节点-> 左子树所有节点(同样根左右)-> 右子树所有节点(同样根节点)

            解决方案:

                    引入队列 空间复杂度O(n):

                            最简思路,按先序遍历的顺序将元素存入队列中 再遍历队列构建链表 空间复杂度O(n)

                    原地算法 空间复杂度O(1):

                            最终所有节点都按先序遍历的顺序挂在根节点的右子树上,不断将每个节点的左子树合并到右子树上即可

                            合并的同时保证先序遍历的顺序;

                            即左子树与右子树的连接点为先序遍历顺序下左子树的最后一个节点(即根节点第一个左子节点最深的右子节点)

                            1.找到当前节点的左子节点(定位到要合并的左子树) 不存在左子节点 则直接移动到右子节点即可

                            2.沿着当前左子节点的right一直移动到尽头即可  即为最后一个节点(链接处)

                            3.链接左子树与右子树,再将链接后的子树变更为根节点的右子树

                            4.迭代到新的右子节点(原树的左子节点)

*/

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //利用栈保存节点
    private Queue<TreeNode> queue = new ArrayDeque<>();

    public void flatten(TreeNode root) {
        /**
            展开后的链表与二叉树的先序遍历顺序相同
            即 链表顺序为 根节点-> 左子树所有节点(同样根左右)-> 右子树所有节点(同样根节点)
            解决方案:
                    引入队列 空间复杂度O(n):
                            最简思路,按先序遍历的顺序将元素存入队列中 再遍历队列构建链表 空间复杂度O(n)
                    原地算法 空间复杂度O(1):
                            最终所有节点都按先序遍历的顺序挂在根节点的右子树上,不断将每个节点的左子树合并到右子树上即可
                            合并的同时保证先序遍历的顺序;
                            即左子树与右子树的连接点为先序遍历顺序下左子树的最后一个节点(即根节点第一个左子节点最深的右子节点)
                            1.找到当前节点的左子节点(定位到要合并的左子树) 不存在左子节点 则直接移动到右子节点即可
                            2.沿着当前左子节点的right一直移动到尽头即可  即为最后一个节点(链接处)
                            3.链接左子树与右子树,再将链接后的子树变更为根节点的右子树
                            4.迭代到新的右子节点(原树的左子节点)
        */

        //原地算法
        TreeNode curr = root;
        while(curr != null) {
            //在保证先序遍历顺序的前提下 将左子树合并到右子树
            if(curr.left != null) {
                //找到先序遍历顺序下左子树的最后一个节点,即最深的右子节点
                TreeNode deepestRight = curr.left;
                while(deepestRight.right != null) { //沿着当前左子节点的right一直移动到尽头即可
                    deepestRight = deepestRight.right;
                }

                //连接左子树与右子树
                deepestRight.right  = curr.right;
                //将新树变更为右树
                curr.right =  curr.left;
                curr.left = null;
            }
            curr  = curr.right;
        }


        /** 队列
        preorder(root);
        构建链表
        while(!queue.isEmpty()) {
            TreeNode node = queue.remove();
            node.right = queue.peek();
            node.left = null;
        }*/
    }

    private void preorder(TreeNode node) {
        if(node == null) {
            return;
        }

        //先序 将当前节点入栈
        queue.add(node);

        //左 右
        preorder(node.left);
        preorder(node.right);
    }
}