二叉树----10.二叉树的右视图

 

题目链接

/**

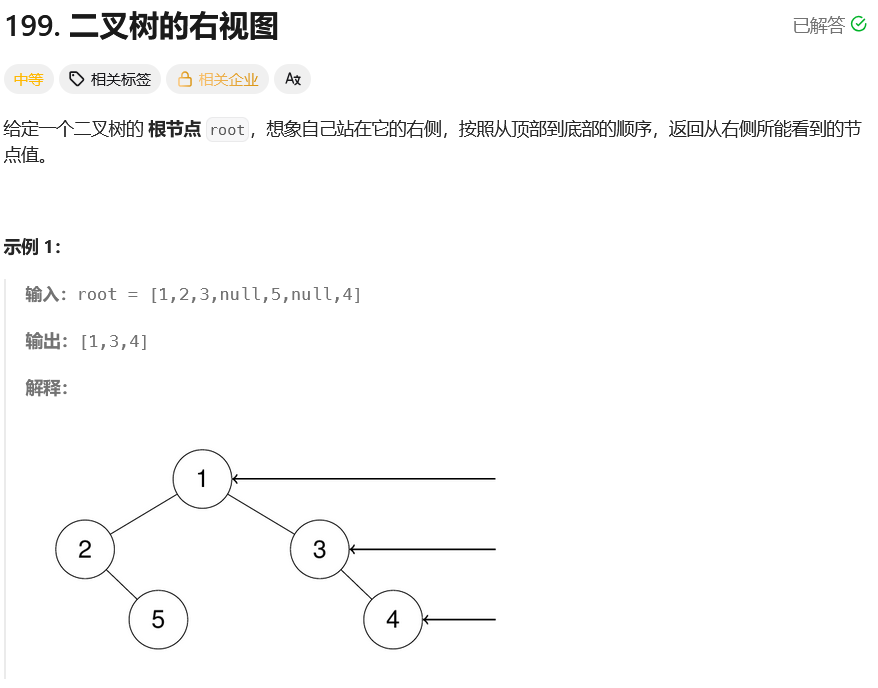
            能看到节点的优先级:

                            右子树外侧 > 右子树内侧 > 左子树内侧 > 左子树外侧;  

                            高优先级节点出现后,低优先级的节点不可见

            输出顺序:

                    从顶部开始按层级输出

            解决方案:

                    迭代法(广度优先):

                                    层序遍历(引入队列) + 优先级限制

                                    按先左后右的顺序入队 每层可见的元素必然是队尾元素,只保存每层队尾元素 其余直接移除即可

                    递归法(深度优先):

                                    按根 右 左的顺序递归遍历

                                    没层递归访问到的第一个元素就是最右侧的元素

*/

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {

    //保存 每层可见的节点
    List<Integer> list = new ArrayList<>();

    public List<Integer> rightSideView(TreeNode root) {
        /**
            能看到节点的优先级: 
                            右子树外侧 > 右子树内侧 > 左子树内侧 > 左子树外侧;  
                            高优先级节点出现后,低优先级的节点不可见
            输出顺序: 
                    从顶部开始按层级输出
            解决方案:
                    迭代法(广度优先): 
                                    层序遍历(引入队列) + 优先级限制
                                    按先左后右的顺序入队 每层可见的元素必然是队尾元素,只保存每层队尾元素 其余直接移除即可
                    递归法(深度优先): 
                                    按根 右 左的顺序递归遍历
                                    没层递归访问到的第一个元素就是最右侧的元素
        */
        
        //迭代法(广度优先)
        //bfs(root); 

        //递归法(深度优先)
        dfs(root,1); 
        return list;
    }

    //迭代(广度优先)
    private void bfs(TreeNode root) {
        if(root == null) {
            return;
        }
        
        //队列
        Queue<TreeNode> queue = new ArrayDeque<>();
        queue.add(root); //初始化

        while(!queue.isEmpty()) {
            //记录当前队列中的元素个数  即当前层中元素个数
            int size = queue.size();

            //遍历当前层 按先左后右的顺序入队 那么可见节点必然是队尾元素
            for(int i = 0; i < size; i++) {
                //出队
                TreeNode node = queue.poll();

                //只有队尾元素才可见保存起来 否则不保存
                if(i == size - 1) {
                    list.add(node.val);
                }

                //添加下一层的元素 提前记录队列中元素的意义, 避免此时的添加混淆各层的元素
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
            }
        }
    }

    //递归(深度优先)
    private void dfs(TreeNode root,int depth){
        if(root == null) {
            return;
        }

        //说明当前层级是第一次遍历到
        if(depth > list.size()) {
            //将当前节点保存
            list.add(root.val);
        }

        //先右 递归时记录当前层数
        dfs(root.right,depth + 1);
        dfs(root.left,depth + 1);
    } 

}