快速排序（1）

于 2025-04-15 14:51:40 发布
阅读量1.1k 收藏 10
点赞数 30
分类专栏： 数据结构初阶 文章标签： 排序算法 算法 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/LXdian_LX/article/details/147250055
版权

快速排序

今天来讲讲快排。整体代码如下：

sort.h

#include <stdio.h>

void PrintArray(int *a,int n);
void Swap(int *x,int *y);

//三数取中
int GetMiddle(int *a,int left,int right);
//原版
int PartSort1(int *a,int left,int right);
//挖坑
int PartSort2(int *a,int left,int right);
//前后指针
int PartSort3(int *a,int left,int right);

//快速排序
void QuickSort(int *a,int left,int right);

sort.c

#include "sort.h"

void PrintArray(int *a,int n)
{
    for(int i=0;i<n;i++)
    {
        printf("%d ",a[i]);
    }
    printf("\n");
}
void Swap(int *x,int *y)
{
    int tmp=*x;
    *x=*y;
    *y=tmp;
}

//三数取中
//取一个不大不小的值，差不多就是中位数的意思,但不完全是中位数，这主要是为了应付有序数列
int GetMiddle(int *a,int left,int right)
{
    int mid=(left+right)/2;
    if(a[mid]>a[left])  //left<mid
    {
        if(a[mid]<a[right])  //left<mid<right
            return mid;
        else if(a[left]<a[right])     //<left<right<mid
            return right;
        else                          //right<left<mid
            return left;
    }
    else  //mid<left
    {
        if(a[mid]>a[right]) //right<mid<left
            return mid;
        else if(a[left]<a[right])  //mid<left<right
            return left;
        else                       //mid<right<left
            return right;
    }

}

//原版
int PartSort1(int *a,int left,int right)
{
    int middle_i= GetMiddle(a,left,right);
    Swap(&a[middle_i],&a[left]);

    int key_i=left;
    while(left<right)
    {
        while(left<right&&a[right]>=a[key_i])
        {
            right--;
        }
        while(left<right&&a[left]<=a[key_i])
        {
            left++;
        }
        Swap(&a[left],&a[right]);
    }
    Swap(&a[key_i],&a[left]);

    return left;
}
//挖坑
int PartSort2(int *a,int left,int right)
{
    int middle_i= GetMiddle(a,left,right);
    Swap(&a[middle_i],&a[left]);

    int key=a[left];
    int hole=left;
    while(left<right)
    {
        while(left<right&&a[right]>=key)
        {
            right--;
        }
        a[hole]=a[right];
        hole=right;
        while(left<right&&a[left]<=key)
        {
            left++;
        }
        a[hole]=a[left];
        hole=left;
    }
    a[hole]=key;
    return hole;
}
//前后指针
int PartSort3(int *a,int left,int right)
{
    int after=left;
    int first=left+1;

    int key_i=left;
    while(first<=right)
    {
        if(a[first]<a[key_i] && after++!=first)
        {
            Swap(&a[after],&a[first]);
        }
        first++;
    }

    Swap(&a[after],&a[key_i]);

    return after;
}

//快速排序
void QuickSort(int *a,int left,int right)
{
    if(left>=right)
        return;

    int key_i= PartSort3(a,left,right);
    QuickSort(a,left,key_i-1);
    QuickSort(a,key_i+1,right);
}

test.c

#include "sort.h"

void Test()
{
    int a[]={6,1,2,7,9,3,4,5,10,8};
    QuickSort(a,0, sizeof(a)/ sizeof(int)-1);
    PrintArray(a, sizeof(a)/ sizeof(int));
}

int main()
{
    Test();
    return 0;
}

Hoare版本快速排序

在这里插入图片描述

代码：

//原版
int PartSort1(int *a,int left,int right)
{
    int key_i=left;
    while(left<right)
    {
        while(left<right&&a[right]>=a[key_i])
        {
            right--;
        }
        while(left<right&&a[left]<=a[key_i])
        {
            left++;
        }
        Swap(&a[left],&a[right]);
    }
    Swap(&a[key_i],&a[left]);

    return left;
}

这里大家可以看看这个动图，这个动图就是原版快速排序的一个主要思想，也就是快速排序中一趟排序的过程。接下来就是画图对这个过程的一个解析：

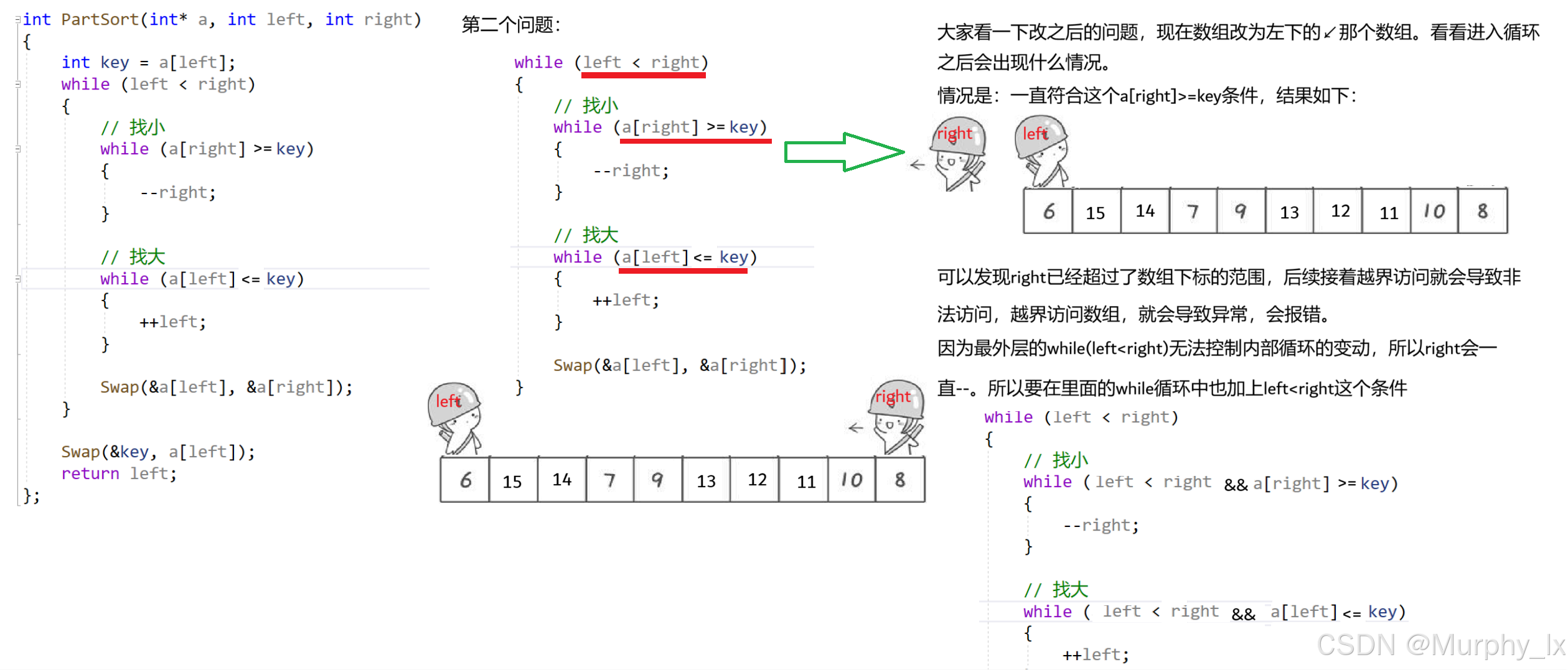
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

通过上面的解析，希望大家已经理解了单趟排序的意义，那么接下来就是完整的一个快速排序：

//原版
int PartSort1(int *a,int left,int right)
{
    int key_i=left;
    while(left<right)
    {
        while(left<right&&a[right]>=a[key_i])
        {
            right--;
        }
        while(left<right&&a[left]<=a[key_i])
        {
            left++;
        }
        Swap(&a[left],&a[right]);
    }
    Swap(&a[key_i],&a[left]);

    return left;
}
//快速排序
void QuickSort(int *a,int left,int right)
{
    if(left>=right)
        return;

    int key_i= PartSort1(a,left,right);
    QuickSort(a,left,key_i-1);
    QuickSort(a,key_i+1,right);
}

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

时间复杂度

  • 最好情况：每次划分都能将数组均匀地分成两部分，此时时间复杂度为 (O(nlogn))。假设数组长度为 n，第一次划分后，左右两个子数组的长度都为 (n/2)，需要 (O(n)) 的时间来划分；接下来对两个子数组分别进行快速排序，时间复杂度为 (2T(n/2))。根据主定理，可得 (T(n)=O(nlogn))。
  • 最坏情况：数组已经有序或基本有序时，每次划分只能减少一个元素，此时时间复杂度退化为 (O(n^{2}))。例如，数组已经升序排列，以第一个元素为基准进行划分，每次划分都只能将数组分成一个元素和 (n - 1) 个元素的两个子数组，需要进行 (n - 1) 次划分，每次划分需要 (O(n)) 的时间，所以时间复杂度为 (O(n^{2}))。
  • 平均情况：在随机情况下，快速排序的平均时间复杂度也是 (O(nlogn))。这是因为在平均情况下，每次划分将数组分成的两个子数组的大小是随机的，虽然不一定正好是 (n/2)，但可以证明其时间复杂度仍然是 (O(nlogn))。

空间复杂度

  • 最好情况：每次划分都能将数组均匀地分成两部分，递归树的高度为 logn，每一层需要的额外空间为 (O(n))，但由于可以复用空间，所以总的空间复杂度为 (O(logn))。
  • 最坏情况：数组已经有序或基本有序时，递归树的高度为 n，需要 (O(n)) 的栈空间来存储递归调用的信息，所以空间复杂度为 (O(n))。
  • 平均情况：平均空间复杂度为 (O(logn))。这是因为在平均情况下，递归树的高度近似为 logn，虽然在不同的划分情况下栈空间的使用会有所不同，但总体上平均空间复杂度仍然是 (O(logn))。

在这里插入图片描述

所以为了改良快速排序在遇到有序数列时候的窘境，出现一个“三数取中”的方法。这个方法的意思就是选择一个大不大不小的数，因为我们选择key值一般都是选择左边嘛，如果是有序数列，比如升序数列，1234，最左边的值就是1，是最小值，就无法把数组分成两份，或者说降序4321，最左边的值是4，是最大值，也无法把数组分成两份。所以我们就选择这个数组中一个不大不小的值，让这个不大不小的值充当key。这样就可以在遇到有序数组的时候很好的将数组分成两份。届时，有序数组就会从最坏的情况变成最好的情况。很好的解决这个问题。

//三数取中
//取一个不大不小的值，差不多就是中位数的意思,但不完全是中位数，这主要是为了应付有序数列
int GetMiddle(int *a,int left,int right)
{
    int mid=(left+right)/2;
    if(a[mid]>a[left])  //left<mid
    {
        if(a[mid]<a[right])  //left<mid<right
            return mid;
        else if(a[left]<a[right])     //<left<right<mid
            return right;
        else                          //right<left<mid
            return left;
    }
    else  //mid<left
    {
        if(a[mid]>a[right]) //right<mid<left
            return mid;
        else if(a[left]<a[right])  //mid<left<right
            return left;
        else                       //mid<right<left
            return right;
    }

}

注释写的也比较清楚了，我们不是一定要找数组中数值最中间的那个数，我们只需要找一个不是最大不是最小的就好了，比如1 2 3 4，只要不是1和4就行，像2和3都是可以选择的，明白吧。然后把这个三数取中放到我们的快速排序里面去：

//三数取中
//取一个不大不小的值，差不多就是中位数的意思,但不完全是中位数，这主要是为了应付有序数列
int GetMiddle(int *a,int left,int right)
{
    int mid=(left+right)/2;
    if(a[mid]>a[left])  //left<mid
    {
        if(a[mid]<a[right])  //left<mid<right
            return mid;
        else if(a[left]<a[right])     //<left<right<mid
            return right;
        else                          //right<left<mid
            return left;
    }
    else  //mid<left
    {
        if(a[mid]>a[right]) //right<mid<left
            return mid;
        else if(a[left]<a[right])  //mid<left<right
            return left;
        else                       //mid<right<left
            return right;
    }

}

//原版
int PartSort1(int *a,int left,int right)
{
    int middle_i= GetMiddle(a,left,right);
    Swap(&a[middle_i],&a[left]);

    int key_i=left;
    while(left<right)
    {
        while(left<right&&a[right]>=a[key_i])
        {
            right--;
        }
        while(left<right&&a[left]<=a[key_i])
        {
            left++;
        }
        Swap(&a[left],&a[right]);
    }
    Swap(&a[key_i],&a[left]);

    return left;
}
//快速排序
void QuickSort(int *a,int left,int right)
{
    if(left>=right)
        return;

    int key_i= PartSort1(a,left,right);
    QuickSort(a,left,key_i-1);
    QuickSort(a,key_i+1,right);
}

那么原版快速排序以及其中一个优化就讲完了，接下来讲的就是与原版类似的别的快速排序，啥意思呢？就是思想是几乎一样的，但是解释方法不同而已，如果已经了解了上面的方法，下面的方法不会有啥难处。这里不同的地方就是单趟排序的解释方法不同：

挖坑法快速排序

在这里插入图片描述

先看动图，这个应该很好理解，如果理解了上面的Hoare的。

//三数取中
//取一个不大不小的值，差不多就是中位数的意思,但不完全是中位数，这主要是为了应付有序数列
int GetMiddle(int *a,int left,int right)
{
    int mid=(left+right)/2;
    if(a[mid]>a[left])  //left<mid
    {
        if(a[mid]<a[right])  //left<mid<right
            return mid;
        else if(a[left]<a[right])     //<left<right<mid
            return right;
        else                          //right<left<mid
            return left;
    }
    else  //mid<left
    {
        if(a[mid]>a[right]) //right<mid<left
            return mid;
        else if(a[left]<a[right])  //mid<left<right
            return left;
        else                       //mid<right<left
            return right;
    }

}

//挖坑
int PartSort2(int *a,int left,int right)
{
    int middle_i= GetMiddle(a,left,right);
    Swap(&a[middle_i],&a[left]);

    int key=a[left];
    int hole=left;
    while(left<right)
    {
        while(left<right&&a[right]>=key)
        {
            right--;
        }
        a[hole]=a[right];
        hole=right;
        while(left<right&&a[left]<=key)
        {
            left++;
        }
        a[hole]=a[left];
        hole=left;
    }
    a[hole]=key;
    return hole;
}

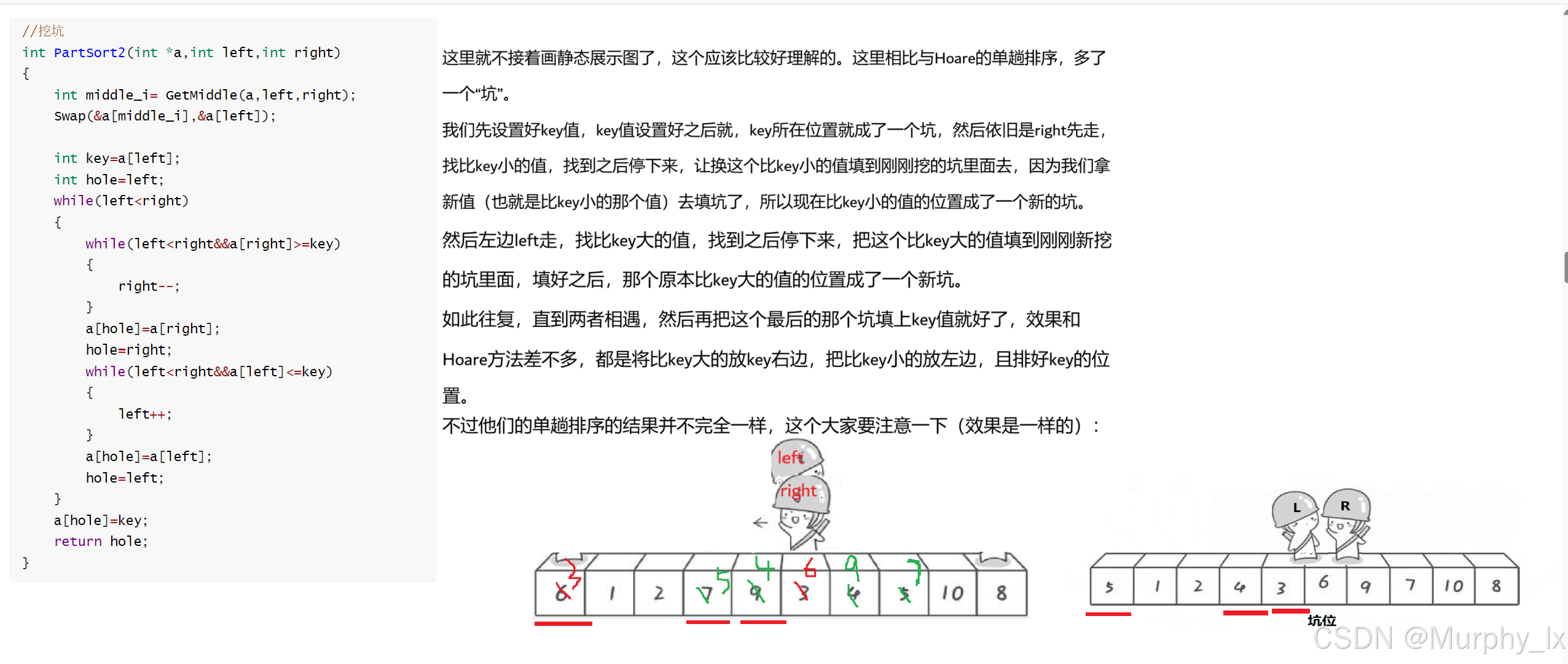
在这里插入图片描述

然后还有一个

前后指针法

动图：
在这里插入图片描述

//三数取中
//取一个不大不小的值，差不多就是中位数的意思,但不完全是中位数，这主要是为了应付有序数列
int GetMiddle(int *a,int left,int right)
{
    int mid=(left+right)/2;
    if(a[mid]>a[left])  //left<mid
    {
        if(a[mid]<a[right])  //left<mid<right
            return mid;
        else if(a[left]<a[right])     //<left<right<mid
            return right;
        else                          //right<left<mid
            return left;
    }
    else  //mid<left
    {
        if(a[mid]>a[right]) //right<mid<left
            return mid;
        else if(a[left]<a[right])  //mid<left<right
            return left;
        else                       //mid<right<left
            return right;
    }

}

//前后指针
int PartSort3(int *a,int left,int right)
{
    int middle_i= GetMiddle(a,left,right);
    Swap(&a[middle_i],&a[left]);
    
    int after=left;
    int first=left+1;

    int key_i=left;
    while(first<=right)
    {
        if(a[first]<a[key_i] && after++!=first)
        {
            Swap(&a[after],&a[first]);
        }
        first++;
    }

    Swap(&a[after],&a[key_i]);

    return after;
}

在这里插入图片描述

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值