Day13|二叉树理论基础、二叉树前中后序遍历、二叉树层序遍历

二叉树理论基础：

1.要知道的4种二叉树：

①满二叉树。除了底层节点度为0，其他所有节点度为2.

②完全二叉树。最底层节点可能没填满，且都集中在最左边，满二叉树属于完全二叉树。

③二叉搜索树。左子树小于根节点，右子树大于根节点

④平衡二叉搜索树。加了平衡2字，左右两个子树的高度差不超过1。

2.存储方式：

①链式存储。包含：节点值、左指针、右指针。

②顺序存储（很少用，了解即可）。数组存储，下标从左到右、从上到下，如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

3.遍历方式：

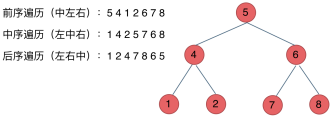
①深度优先遍历：先往深走，遇到叶子节点再往回走。不撞南墙不回头。

前中后，其实指的就是中间节点的遍历顺序。

②广度优先遍历：层序遍历。

144.二叉树的前序遍历

94.二叉树的中序遍历

145.二叉树的后序遍历

Ⅰ二叉树递归遍历

①确定递归函数的参数和返回值

②确定终止条件

③确定单层递归的逻辑

Ⅱ二叉树的迭代遍历

Ⅲ二叉树的统一迭代法

这几天情绪一直紧绷着，连“感觉”也钝化了，也不知道自己在烦什么。这次先放下，跳过这两个稍微有点难度的，过后一定补上。

层序遍历

102.二叉树的层序遍历(opens new window)

自己的思考：用了两个队列交替完全弹出操作。

class Solution {
public:
    void travesal(queue<TreeNode*>& q1, queue<TreeNode*>& q2, vector<int>& v) {
        TreeNode* node = q1.front();
        v.push_back(node->val);
        if(node->left != nullptr) q2.push(node->left);
        if(node->right != nullptr) q2.push(node->right);
        q1.pop();
    }

    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> v;
        if (root == nullptr) return v;
        queue<TreeNode*> q1, q2;
        q1.push(root);
        int i = 0;
        while (!q1.empty() || !q2.empty()) {
            vector<int> vec;
            v.push_back(vec);
            if (!q1.empty()) {
                while (!q1.empty()) travesal(q1, q2, v[i]);
                i++;
            }
            else {
                while (!q2.empty()) travesal(q2, q1, v[i]);    
                i++;         
            }
        }
        return v;
    }
};

参考解法：用了size来记录某层的节点数量，节省一个队列，其他地方基本一致。

107.二叉树的层次遍历II

199.二叉树的右视图

637.二叉树的层平均值

429.N叉树的层序遍历

下面5道题（都看过题目了，没做）没啥新点，会写层遍历方法就能写。

515.在每个树行中找最大值

116.填充每个节点的下一个右侧节点指针

117.填充每个节点的下一个右侧节点指针II

104.二叉树的最大深度

111.二叉树的最小深度