容斥原理求解算法-优快云博客

传送门

求指定区间内与n互素的数的个数：

给出整数n和r。求区间[1;r]中与n互素的数的个数。

去解决它的逆问题，求不与n互素的数的个数。

考虑n的所有素因子pi(i=1…k)

在[1;r]中有多少数能被pi整除呢？它就是：

然而，如果我们单纯将所有结果相加，会得到错误答案。有些数可能被统计多次（被好几个素因子整除）。所以，我们要运用容斥原理来解决。

我们可以用2^k的算法求出所有的pi组合，然后计算每种组合的pi乘积，通过容斥原理来对结果进行加减处理。

既然要找的是1-r中与n互素的数字的个数，找互素的数字不好找，那么可以思考逆向求解，找与n有共同因子的数字的个数，这样用总的数字减掉找到的有共同因子的数字的个数，就是我们要求的与n互素的数字的个数。

那么求与n有共同因子的数字该怎么求呢？？

首先，先找出2-n以内n的基本因子。
然后再找1-r中与n有相同基本因子的数字，计数。
找出所有与n有共同因子的数字个数之后
用总数减去与n有共同因子的数字个数
就是我们要求的数字的个数

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
#include<string.h>
#include<vector>
using namespace std;
int n,r;
int solve(int n,int r)
{
   vector<int>p;
   for(int i=2;i*i<=n;++i)
   {
       if(n%i==0)
	   {
	      p.push_back(i);
		  while(n%i==0)
		  {
		     n=n/i;		  	
		  }

	   } 	
   }
	   if(n>1)
	      p.push_back(n); 

	   int sum=0;
	   for(int msk=1;msk<(1<<p.size());++msk)
	   {
	      int mult=1,bits=0;
		   
		  for(int i=0;i<(int)p.size();++i)
		  {
		     if(msk & (1<<i)) //目的在于找到所有的因子
		     {
		     	++bits;
		     	mult*=p[i];
			 }		  	
		  }

		  int cur=r/mult; //求个数
		  if(bits%2==1)
		  {
		  	  sum+=cur;
		  }
		  else
		      sum-=cur;
	   }

	   return r-sum;	
} 
int main()
{
	while(scanf("%d%d",&n,&r)!=EOF)
	{
	cout<<solve(n,r)<<endl;		
	}
	return 0;
}

HDU 1796 How many integers can you find

题意：求在1-（n-1）中，能够被给定序列中的任意数字整除的数字的个数。

注意：

用 long long
当输入是0的时候就不再考虑

上一个自己写的错误代码

/*
#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
#include<string.h>
#include<vector>
using namespace std;
typedef long long int ll;
ll q[20];
ll solve(ll n,ll r)
{
	vector<ll>p;
	for(int i=0;i<n;i++)
	{
		p.push_back(q[i]);
	}
	//for(int i=0;i<p.size();i++)
	//printf("%d ",p[i]);
    ll sum=0;
	for(int msk=1;msk<(1<<p.size());msk++)
	{
	  ll bits=0,mult=1;
	  for(int i=0;i<p.size();i++)
	  {
	  	  if(msk & (1<<i))
	  	  {
	  	      bits++;
			  mult*=p[i];	
		  }
	  }
	  ll cur=r/mult;
	  if(bits%2==1)
	  {
	  	sum+=cur; 
	  }
	  else{
	  	sum-=cur;
	  }
	}
 return sum;
} 
int main()
{
	ll n,m;
	while(cin>>n>>m){
		ll sum=0;
	for(int i=0;i<m;i++)
	{
		ll x;
		cin>>x;
		if(x>0)
		 q[i]=x;
	}
	sum+=solve(m,n-1);
	cout<<sum<<endl;		
	}
	return 0;
} */

上一个别人写的正确代码

#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <cstdio>
using namespace std;
#define INT long long
const int N = 12;
INT p[N];
INT gcd(INT a, INT b)
{
    if(b == 0) return a;
    return gcd(b, a % b);
}
 
INT lcm(INT a, INT b)
{
    return a * b / gcd(a, b);
}
 
INT solve(INT n, INT m)
{
    INT ans = 0;
    for(INT i = 1; i < (1 << m); i ++){
        INT cnt = 0, tmp = 1;
        for(INT j = 0; j < m; j ++){
            if(i & (1 << j)){
                cnt ++;
                tmp = lcm(tmp, p[j]);
            }
 
        }
        if(cnt % 2) ans += n / tmp;
        else ans -= n / tmp;
    }
    return ans;
}
 
int main()
{
    INT n, m;
    while(cin >> n >> m){
        INT t = 0, x;
        for(INT i = 0; i < m; i ++){
            cin >> x;
            if(x > 0) p[t ++] = x;
        }
        m = t;
        cout << solve(n - 1, m) << endl;
    }
    return 0;
}

T^TOJ 2332 电灯泡

V_Dragon有n栈电灯泡，编号为1-n，每个灯泡都有一个开关。那么问题来了

所有灯泡初始时为不亮的

V_Dragon分别进行三次操作

每次操作他都选一个质数x，将编号为x和x的整数倍的灯泡的开关都拨动一下（如果灯为亮，那么拨动以后灯为不亮,如果灯不亮，拨动以后变为亮）

求最后亮着的灯的数量

起初给出三个灯都是不亮的，当按一次之后，灯就全部亮了。按两次之后，灯就熄灭了。这样就可以总结出一个规律：按奇数次的时候，灯是亮的；按偶数次的时候，灯是熄灭的。

下面用一个容斥定理的例子来解释这个问题。

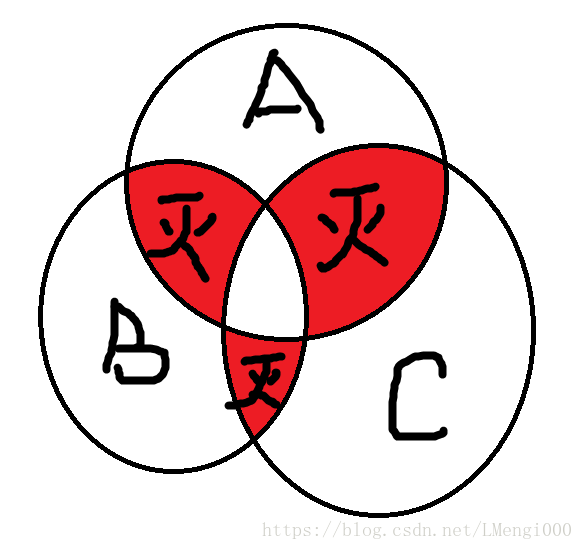
设S=（A∪B∪C）=A +B+C-(A∩B+A∩C+B∩C)+(A∩B∩C)

A +B+C，把A、B、C中所有的数字都加了一遍，包括A∩B、A∩C、B∩C 重叠的部分。
加A的时候，加了一次A∩B，加B的时候，加了一次A∩B，这样就加了两次A∩B，A∩B这一部分是熄灭的，不是我们最终想要的结果，因此，要把加上的这两次都减去。
A∩C、B∩C同理，加上的两次都要减去。
加A的时候，加了一次A∩B∩C，加B、C的时候也是加了一次A∩B∩C，这样就是加了3次A∩B∩C。
减A∩B的时候，减了两次，A∩B∩C也是减了两次，同理减A∩C、B∩C的时候，都是各减两次，这样就是减了6次
A∩B∩C是按了奇数次的，我们应当保留一次，所以 +3-6=-3，最后应当加上四倍的A∩B∩C。

上图中的空白部分就是要求的数字。


#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
#include<string.h>
#include<vector>
using namespace std;
typedef long long int ll;
ll t,n,a,b,c;
int main()
{
	scanf("%lld",&t);
	while(t--)
	{
		scanf("%lld",&n);
		scanf("%lld%lld%lld",&a,&b,&c);
		ll sum=n/a+n/b+n/c-2*((n/(a*b))+(n/(a*c))+(n/(b*c)))+4*(n/(a*b*c));
		cout<<sum<<endl;
//由于题目要求，数字之间是互质的，所以任意两个数字之间的最大公因数就是1
//如果没有互质这一个前提条件的话
// (n*gcd(a,b)/a*b) n是要乘上一个最大公因数
//int 时还可以这样写 int sum=n/a+n/b+n/c-2*(n/a/b+n/a/c+n/b/c)+4*(n/a/b/c); 
	}
	return 0;
}