HihoCoder第十二周——树上DP

最新推荐文章于 2024-04-23 10:17:44 发布

原创最新推荐文章于 2024-04-23 10:17:44 发布 · 531 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#dp #算法

DP 同时被 2 个专栏收录

5 篇文章

订阅专栏

hihoCoder

4 篇文章

订阅专栏

这篇博客讨论了如何在树形结构中使用动态规划（DP）策略，以求得最大权值和。作者首先介绍了问题背景，给定一棵树，每个节点带有权值，目标是选择一部分节点进行涂漆，使得涂漆节点的权值和最大。接着，分析了DP的状态转移方程，定义了f(t, m)表示以节点t为根的子树中，选取包含t的m个连通节点的最大权值。最后，提供了具体的代码实现来解决这个问题。" 84915050,7411278,Visual Paradigm IT项目管理框架详解,"['项目管理', '框架', 'IT项目管理', 'Visual Paradigm']

刷油漆

题目

给定一棵树，每个节点有一个权值，将包含1号结点的一部分连通的结点进行涂漆（这里的连通指的是这一些涂漆的结点可以互相到达并且不会经过没有涂漆的结点），使权值和最大。

分析

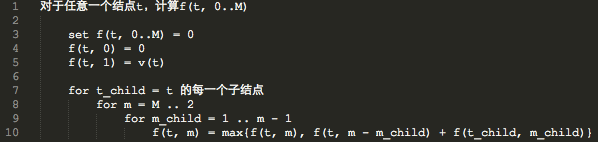
f(t, m)表示，在以t为根的一棵树中，选出包含根节点t的m个连通的结点，能够获得的最高的评分，然后我们的答案就是f(1, M)。
针对于每一个t，同时求解它的f(t, 0..M)，这样的话，我就可以把m视作背包容量，把每个子结点t_child都视作一件单位重量为1的物品，但是和背包问题不同的是，这件物品的总价值并不是单位价值乘以总重量，而是重量为m_child的该物品的价值为f(t_child, m_child)
树上DP

代码

#include <stdio.h>
#include <string.h>
#include <vector>
#include <iostream>
using namespace std;

int n, m, a[101], p[101][101], s, t, used[101];
vector<int> v[101];

void dfs(int k)
{
    for(int i=0; i<v[k].size(); ++i)
    {
        if(used[v[k][i]])
            continue;
        used[v[k][i]] = 1;
        dfs(v[k][i]);
        for(int j=m; j>0; --j)
        {
            for(int x=j; x>0; --x)
                p[k][j] = max(p[k][j],p[k][j-x]+p[v[k][i]][x]);
        }
    }
    for(int i=m; i>0; --i)
        p[k][i] = p[k][i-1] + a[k-1];
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i=0; i<n; ++i)
        scanf("%d", a+i);
    for(int i=0; i<n-1; ++i)
    {
        scanf("%d%d", &s, &t);
        v[s].push_back(t);
        v[t].push_back(s);
    }
    used[1] = 1;
    dfs(1);
    cout<<p[1][m]<<endl;
}