120. Triangle 三角形最少花费路径

问题：

给出三角形数组，从顶层到底层每层找出一个数连接成一条路径，找出一条和最小的路径，要求路径中两层的数必须相邻。

思路：
从倒数第二层开始，用当前层中的每个数+下层的最短路径，就是一个从当前数开始向下的最短的路径，以供上一层选择。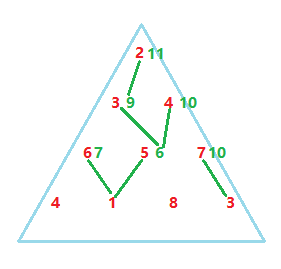

 

代码：

新建一个长度为三角形数组层数的数组a[N]，先将最底一层的数填入，作为初始的最短路径；

从底至顶

每一层中的每个数+下层中相邻两个数中最短的路径，变成了一个子最短路径，可用来让上一层选择。

int minimumTotal(vector<vector<int>>& triangle) {
    int N=triangle.size();
    int a[N];  
    for(int i=0;i<N;i++)
    {
        a[i]=triangle[N-1][i];  //初始最短路径和
    }

    for(int i=N-2;i>=0;i--)  //从倒数第二层到顶层
    {
        for(int j=0;j<=i ;j++) {
             //每层的每个数加上下一层中最短的路径和作为当前层当前数的最短路径和
            a[j]=triangle[i][j]+fmin(a[j], a[j+1]);
            //当前数最短路径和         //下层相邻数最短路径和1   //下层相邻数最短路径和2
        }
    }
    return a[0];

}

参考：https://www.cnblogs.com/liujinhong/p/5551932.html