比较坐标系之间的差异

        在检测中，点线面，面面面，面圆圆建立坐标系是一种常见的做法。但是有些复杂的工件并没有相应的点线面用来建立坐标系，因为工件的本身都是一些曲面，那么为了保证检测的一致性和为了使检测结果能符合对功能或者制程的控制，那么在建立坐标系的时候就需要去定义规定的点或者特殊的几何元素去建立坐标系，比如曲线和曲面。

        简单的来介绍一下点建立坐标系的原理：实际上就是在空间坐标下，用点去约束整个工件，用点去拟合我们CAD模型的坐标系。但是在实际探测的过程中，第一次的探测不可能准确的采集到名义的坐标点。但是通过这几个实际探测点的采集我们是可以计算出一个初步的坐标系，那么在这个坐标系下我们就可以计算出实际点和名义的之间的差异。所以通过多次迭代我们可以约束这个差异，最终的目标是使差异最小，最理想的状态是接近0.

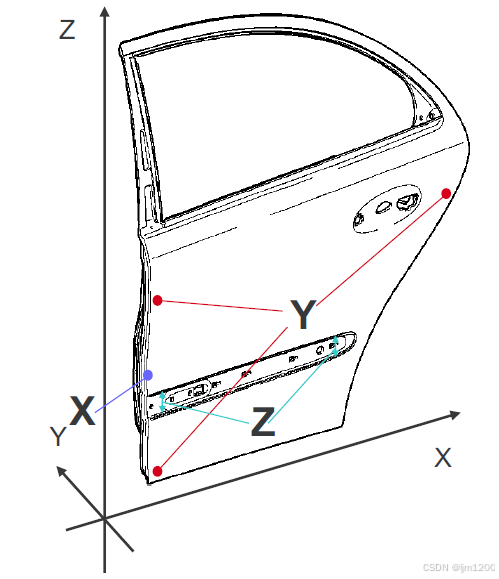
所以拟合状态好坏，我们可以计算实际点和名义点的空间偏差。

        但是在软件中关于坐标系的最佳拟合，怎么判断当前坐标系是否拟合到目标坐标系。我们使用了一个value A的指标。对这个ValueA传统意义上的解释是，这是两个坐标系之间的差异，是一个综合的数值不仅是坐标方向上还有坐标原点上的差异。

        怎么判断这个差异的大小是否符合要求呢？ 简单的想法肯定是越小越好，但是实际的工件的加工偏差，不可能完全使实际坐标系完全拟合到理论坐标系上，那到底拟合到多少才是符合要求呢？一般的拟合原则是1/10法则，就是工件图纸最小公差的1/10。但是这也要考虑工件的加工状况，因为拟合的数据越小，拟合的时间就会越久，所以也要考虑到精度和时间效益的平衡。

        我们再次回到这个拟合差异到底是什么的问题？在回答这个问题之前我们先要讲明白坐标系到底是什么？在坐标坐标计算中，坐标系实际上是一个单位矩阵

任何的数据乘以单位矩阵，还保持原来的数据。

如果我们把这个矩阵再增加一列写成如下的格式

把坐标变换的形式写成下面的形式

那么两个坐标系的差异就可以简单的写为

如果坐标系完全一样，ValueA 数值是{1+1+1-3}+0，当然如果有差异就是{x+y+z-3}+原点变动量