二分模板2_二分模板 returnleft-优快云博客

本文链接：https://blog.youkuaiyun.com/LEewhITe2003/article/details/121608826

这篇博客探讨了二分查找算法的应用，详细解释了如何在有序数组中使用二分查找法寻找目标值，并指出在处理旋转数组时需要注意防止错误的转折点判断。文章强调了在旋转数组中找到最小元素时，避免使用‘找下降’的策略，以防错过搜索点。同时，博主指出了代码实现中的关键细节，如防止整数溢出和确保索引的有效性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

模板2

int binarySearch(vector<int>& nums, int target){
  if(nums.size() == 0)
    return -1;

  int left = 0, right = nums.size();"这里right是nums.size(),故意越界"
  while(left < right){
    // Prevent (left + right) overflow
    int mid = left + (right - left) / 2;
    if(nums[mid] == target){ return mid; }
    else if(nums[mid] < target) { left = mid + 1; }
    else { right = mid; }
     "else没给出这里的条件，应该是nums[mid]>=target，"
    "所以mid可能等于nums[mid],所以要做最后的尾处理"
  }

  // Post-processing:
  // End Condition: left == right
  if(left != nums.size() && nums[left] == target) return left;
    "先判断left的索引值是否合法，然后再判断最后一个元素是否是目标元素"
  return -1;
}

另外一种写法，要注意mid的写法有了不同，是为了跳出循环（最后一步，left和right相邻的时候，mid按照原先的写法（mid=left+(right-left)/2)就等于left本身，而left=mid起到了同样的效果，mid和left不动，陷入死循环了。）

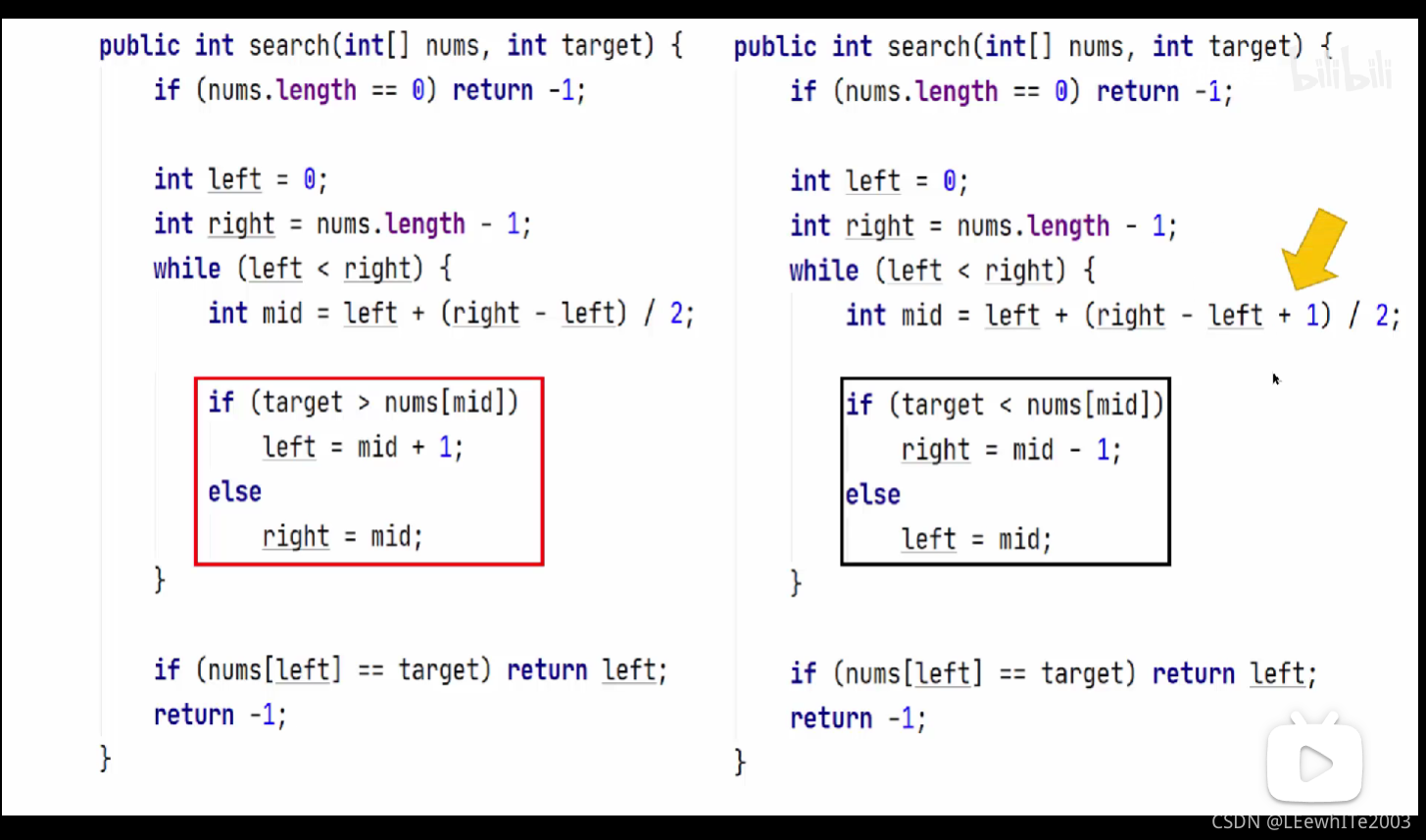
PS：这幅图中，最后的nums[left]前没有判断索引值 “left” 是否合法，这里应该要判断的，图上漏了。

旋转数组最小元素

先说思路，基本思路就是，不断和第一个数或者最后一个数作比较，找到转折点。

注意：这里千万不能通过“找下降”的思想去找转折点，因为如果你的判断条件是“nums[mid]>nums[mid+1]”这样会跳过一些搜索点，致使整个搜索失败。

class Solution {
public:
    int findMin(vector<int>& nums) {
        int left=0,right=nums.size()-1,mid=left+(right-left)/2;
        while(left<right){
            if(nums[mid]>=nums[0])
                left=mid+1;
            else
                right=mid;
            mid=left+(right-left)/2;
        }
        if(right==nums.size()-1&&nums[right]>nums[0])
            return nums[0];
        return nums[left];
    }
};

这里使用模板2进行解题，但是呢，这里有个细节一直被忽略了，那就是"nums[mid]>=nums[0]"，

这里的"="十分重要，如果没有等于号，那么测试数据“2，1”是过不了的。