排序思路:抽象实现多个桶用来储存所需要排序的基数,再递归的调用到每一次数上(通俗点讲,先按个位进行分类,再按十位进行分类,依次排到最高位,最后将所有分类的数连在一起就是排完的序列)
优点:在合适的条件下能实现近乎线性的时间复杂度
缺点:开辟大量的桶可能造成空间上的浪费
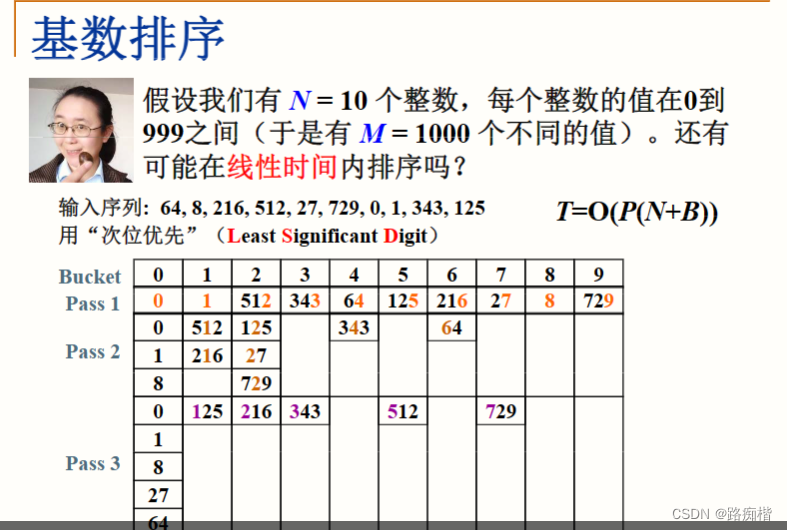
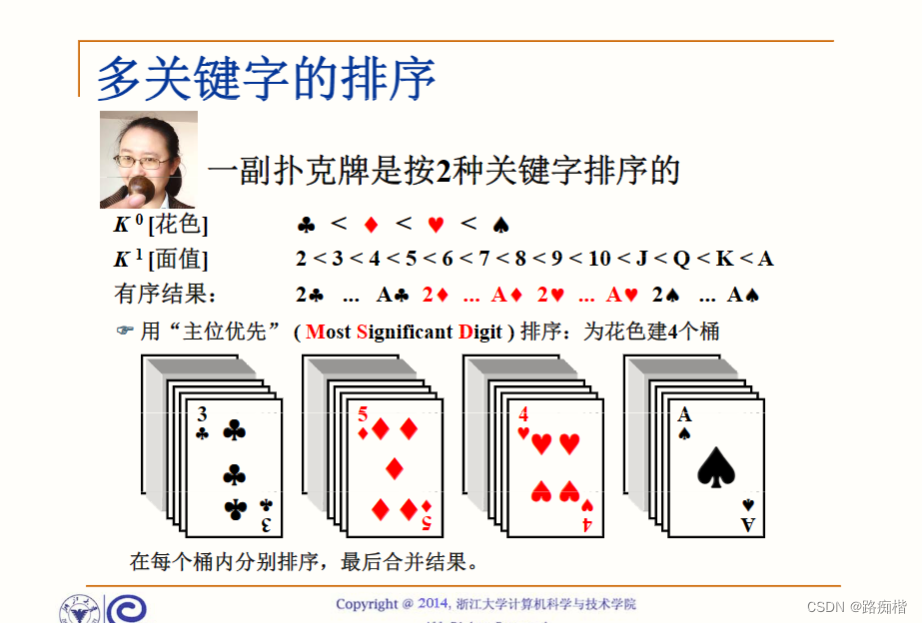
 本文介绍了基数排序的基本思想,利用多个桶对数字按位进行分类,可实现接近线性的时间复杂度,但可能会占用较多空间。
本文介绍了基数排序的基本思想,利用多个桶对数字按位进行分类,可实现接近线性的时间复杂度,但可能会占用较多空间。
排序思路:抽象实现多个桶用来储存所需要排序的基数,再递归的调用到每一次数上(通俗点讲,先按个位进行分类,再按十位进行分类,依次排到最高位,最后将所有分类的数连在一起就是排完的序列)
优点:在合适的条件下能实现近乎线性的时间复杂度
缺点:开辟大量的桶可能造成空间上的浪费



 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


