牛客-k进制

说实话，这道题真的让我很挫败。

写了一个多小时，好不容易测试样例都过了结果提交之后就对了2个，其他都是错误跟超时。

早上又花了4个小时，把每个函数都单独测了一遍，都没啥问题，但是还是不行。

想看题解也都是用C++写的，很奔溃。

虽然没过，但是这个题用到的知识点挺不错的，涉及了进制转换，位数排列。

只学了C的小伙伴也可以参考一下（仅供参考），以后有机会再看看怎么该（累了）。也希望能有大佬帮我看看问题出在哪里。

 

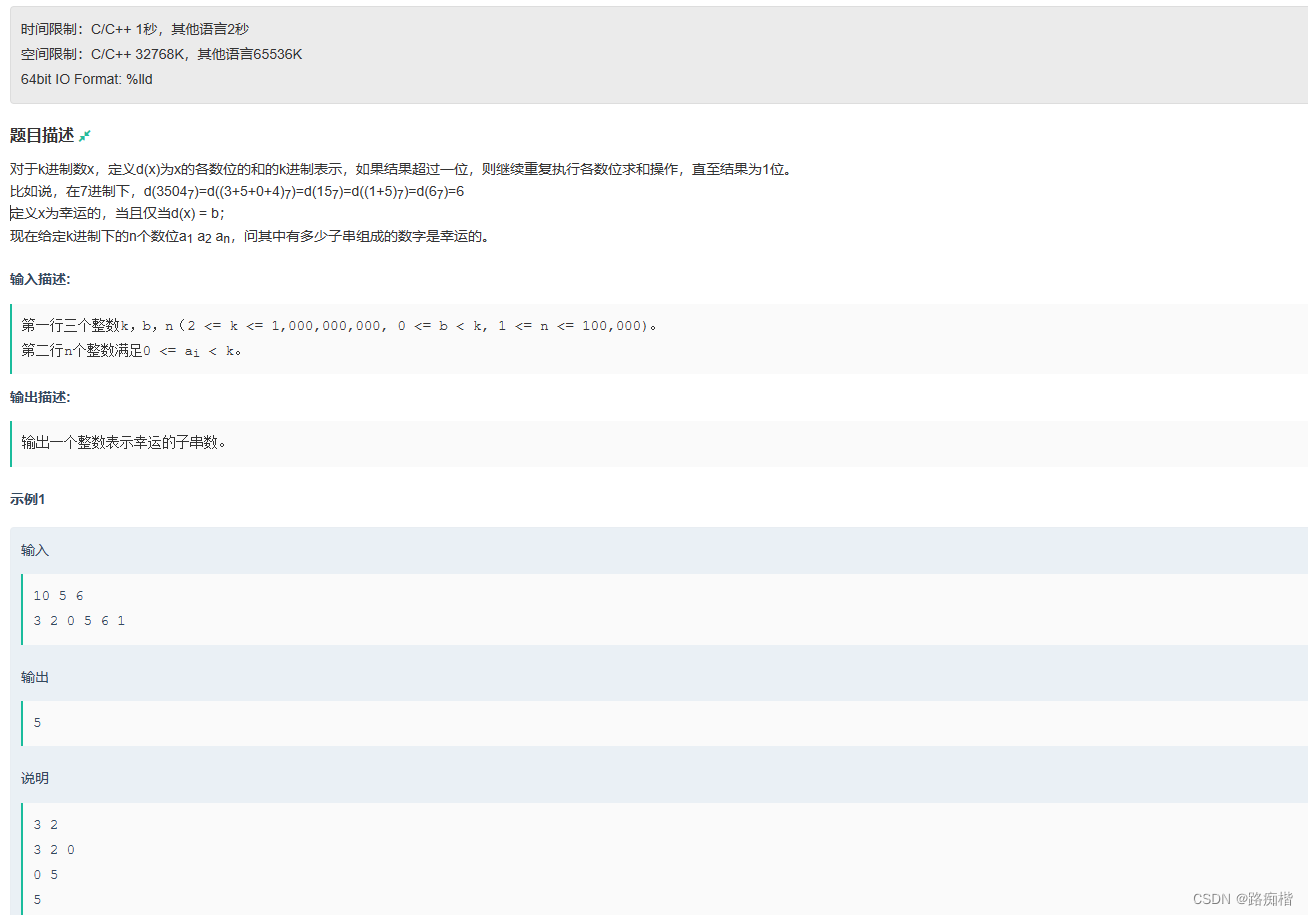
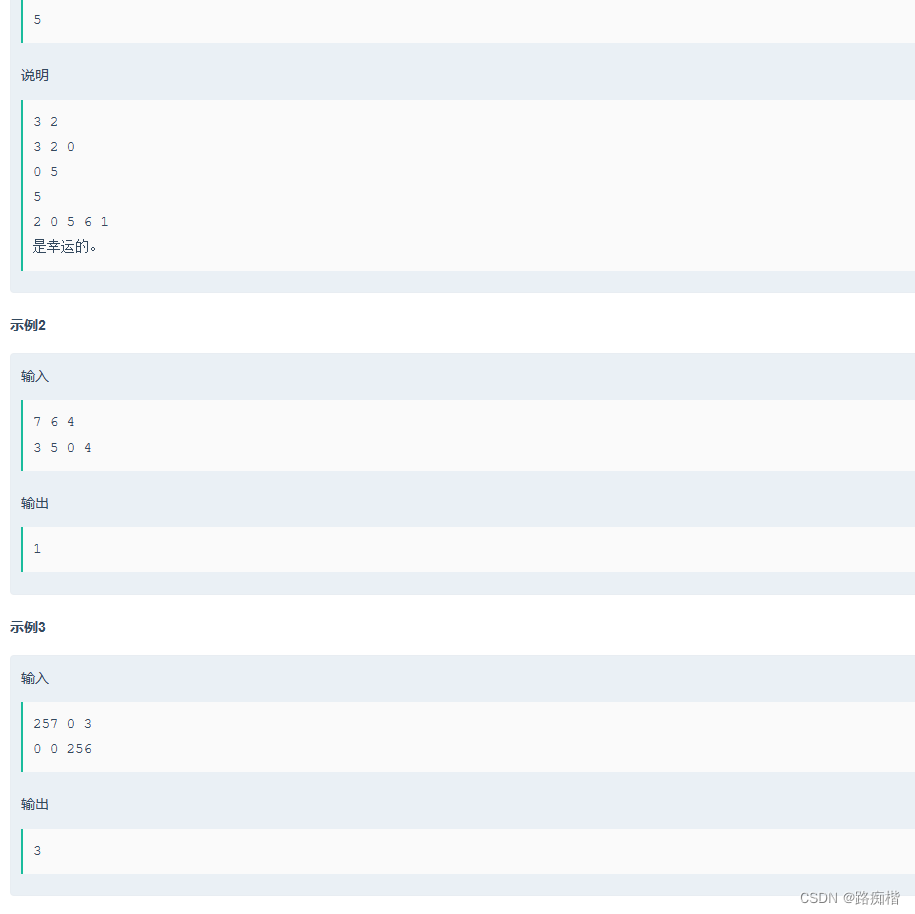
上代码

#include<stdio.h>
#include<stdlib.h>
int jinzhi(int k, int n)
{
    int sum = 0;
    int i = 0;

    int jg = 0;
    for (; n > 0; n /= 10)
    {
        sum += n % 10;
    }
    for (i = 1; sum > 0; i *= 10)
    {
        jg = jg + (sum % k * i);
        sum /= k;
    }
    // printf("   %d   ",jg);
    return jg;
}

int zuheshu(int k, int* num, int n, int b)
{
    int tmp = 0;//组合结果数
    int cnt = 0;
    for (int i = 0; i < n; i++)
    {
        tmp = 0;
        for (int j = i; j < n; j++)
        {

            int tmp2 = 0;//化简结果数
            int tmp_ws = num[j], ws;//判断输入数组的位数
            for (ws = 1; tmp_ws > 0; ws *= 10)
            {
                tmp_ws /= 10;
            }
            tmp *= ws;

            tmp += num[j];
            tmp2 = tmp;
            while (tmp2 > k)
            {
                tmp2 = jinzhi(k, tmp2);
            }
            if (tmp2 == b)
            {
                cnt++;
                //    printf("幸福数：%d\n",tmp);
            }
            //tmp *= 10;//这里有点问题！！！若K的值是大于10则不成立
        }
    }
    return cnt;
}

int main()
{
    int k, b, n;
    int* num;
    int j;
    scanf("%d %d %d", &k, &b, &n);
    num = (int*)malloc(sizeof(int) * n);
    for (int i = 0; i < n; i++)
    {
        scanf("%d", &num[i]);
    }
    j = zuheshu(k, num, n, b);

    printf("%d", j);

    return 0;
}