快速寻找9位数内的自幂数

首先了解自幂数的定义，自幂数是指一个 n 位数，它的每个位上的数字的 n 次幂之和等于它本身。(例如:当n为3时，有1 ^ 3 + 5 ^ 3 + 3 ^ 3 = 153，153即是n为3时的一个自幂数)
自幂数包括:独身数、水仙花数、四叶玫瑰数、五角星数、六合数、北斗七星数、八仙数、九九重阳数、十全十美数。
先介绍基本的方法，代码如下：

#include <stdio.h>
#include <time.h>
#include <math.h>

#include "Nmec.h"

boolean isSelfPower(int num);
int intLen(int num);

boolean isSelfPower(int num) {
	int n;
	int len;
	int sum = 0;

	len = intLen(num);
	for (n = num; n; n /= 10) {
		sum += pow(n % 10, len);
	}

	return num == sum;
}

int intLen(int num) {
	int cnt = 0;

	while(num) {
		cnt++;
		num /= 10;
	}

	return cnt;
}

int main() {
	int maxNum;
	int i;
	long startTime;
	long endTime;
	long deltaTime;

	printf("请输入数值范围:");
	scanf("%d", &maxNum);

	startTime = clock();
	for (i = 0; i < maxNum; i++) {
		if (isSelfPower(i)) {
			printf("%d是自幂数\n", i);
		}
	}
	endTime = clock();
	deltaTime = endTime - startTime;
	printf("耗时:%ld.%03lds", deltaTime / CLOCKS_PER_SEC, deltaTime % CLOCKS_PER_SEC);

	return 0;
}

代码中的头文件 **“Nmec.h”**内容如下:

#ifndef _NMEC_H_
#define _NMEC_H_

typedef unsigned char boolean;

#define TRUE	1
#define FALSE   0
#define NOT_FOUND   -1

#endif

按照这个方法寻找9位数内的自幂数， 所需时间很长，等了6分钟就没在等。 下面介绍一种可以在一分半内找出9位数内的自幂数，话不多说放代码:

#include <stdio.h>
#include <time.h>

#include "Nmec.h"

const int array[][10] = {
	0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 
	0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
	0, 1, 2*2, 3*3, 4*4, 5*5, 6*6, 7*7, 8*8, 9*9,
	0, 1, 2*2*2, 3*3*3, 4*4*4, 5*5*5, 6*6*6, 7*7*7, 8*8*8, 9*9*9,
	0, 1, 2*2*2*2, 3*3*3*3, 4*4*4*4, 5*5*5*5, 6*6*6*6, 7*7*7*7, 8*8*8*8, 9*9*9*9,
	0, 1, 2*2*2*2*2, 3*3*3*3*3, 4*4*4*4*4, 5*5*5*5*5, 6*6*6*6*6, 7*7*7*7*7, 8*8*8*8*8, 9*9*9*9*9,
	0, 1, 2*2*2*2*2*2, 3*3*3*3*3*3, 4*4*4*4*4*4, 5*5*5*5*5*5, 6*6*6*6*6*6, 7*7*7*7*7*7, 8*8*8*8*8*8, 9*9*9*9*9*9,
	0, 1, 2*2*2*2*2*2*2, 3*3*3*3*3*3*3, 4*4*4*4*4*4*4, 5*5*5*5*5*5*5, 6*6*6*6*6*6*6, 7*7*7*7*7*7*7, 8*8*8*8*8*8*8, 9*9*9*9*9*9*9,
	0, 1, 2*2*2*2*2*2*2*2, 3*3*3*3*3*3*3*3, 4*4*4*4*4*4*4*4, 5*5*5*5*5*5*5*5, 6*6*6*6*6*6*6*6, 7*7*7*7*7*7*7*7, 8*8*8*8*8*8*8*8, 9*9*9*9*9*9*9*9,
	0, 1, 2*2*2*2*2*2*2*2*2, 3*3*3*3*3*3*3*3*3, 4*4*4*4*4*4*4*4*4, 5*5*5*5*5*5*5*5*5, 6*6*6*6*6*6*6*6*6, 7*7*7*7*7*7*7*7*7, 8*8*8*8*8*8*8*8*8, 9*9*9*9*9*9*9*9*9,
};

boolean isSelfPower(int num);
int intLen(int num);
int numPower(int a, int p);

boolean isSelfPower(int num) {
	int n;
	int len;
	int sum = 0;

	len = intLen(num);
	for (n = num; n; n /= 10) {
	sum += numPower(n % 10, len);		
	}

	return num == sum;
}

int intLen(int num) {
	if (num < 0) {
		return 0;
	}
	if (num >= 100000000 && num <= 999999999) {
		return 9;
	}
	if (num >= 10000000 && num <= 99999999) {
		return 8;
	}
	if (num >= 1000000 && num <= 9999999) {
		return 7;
	}
	if (num >= 100000 && num <= 999999) {
		return 6;
	}
	if (num >= 10000 && num <= 99999) {
		return 5;
	}
	if (num >= 1000 && num <= 9999) {
		return 4;
	}
	if (num >= 100 && num <= 999) {
		return 3;
	}
	if (num >= 10 && num <= 99) {
		return 2;
	}
	return 1;
}

int numPower(int a, int p) {
	return array[p][a];
}

int main() {
	int maxNum;
	int i;
	long startTime;
	long endTime;
	long deltaTime;

	printf("请输入数值范围:");
	scanf("%d", &maxNum);

	startTime = clock();
	for (i = 0; i < maxNum; i++) {
		if (isSelfPower(i)) {
			printf("%d是自幂数\n", i);
		}
	}
	endTime = clock();
	deltaTime = endTime - startTime;
	printf("耗时:%ld.%03lds", deltaTime / CLOCKS_PER_SEC, deltaTime % CLOCKS_PER_SEC);

	return 0;
}

第二种方法程序运行结果如下：

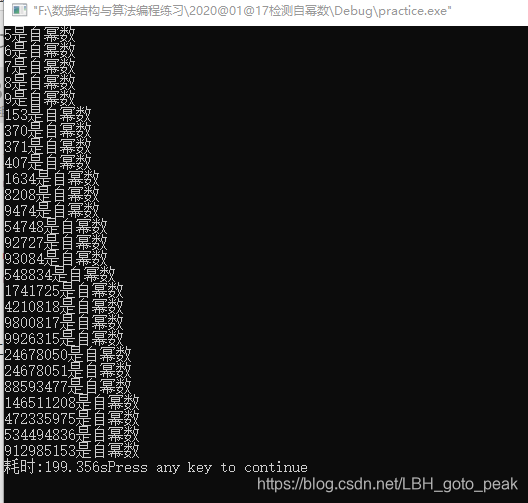
由此可见，第二种方法出结果速度明显加快。对于比较好的机子，可以将时间控制在一分半内。
至此，我的第一篇博文就此问世，在此感谢教主的教诲。