【递推】P1028 数的计算

最新推荐文章于 2024-12-14 11:22:28 发布

原创最新推荐文章于 2024-12-14 11:22:28 发布 · 247 阅读

0 ·

CC 4.0 BY-SA版权

本文解析洛谷P1028题目，介绍了一种通过递归求解的方法，但指出其在大数据时会超时。随后提出了两种优化方案：一是预计算并存储1000种答案；二是通过观察递归结果找出规律，采用递推公式高效求解。最终给出了基于规律的递推解法代码。

题目链接：https://www.luogu.com.cn/problem/P1028

考点：找规律，递推

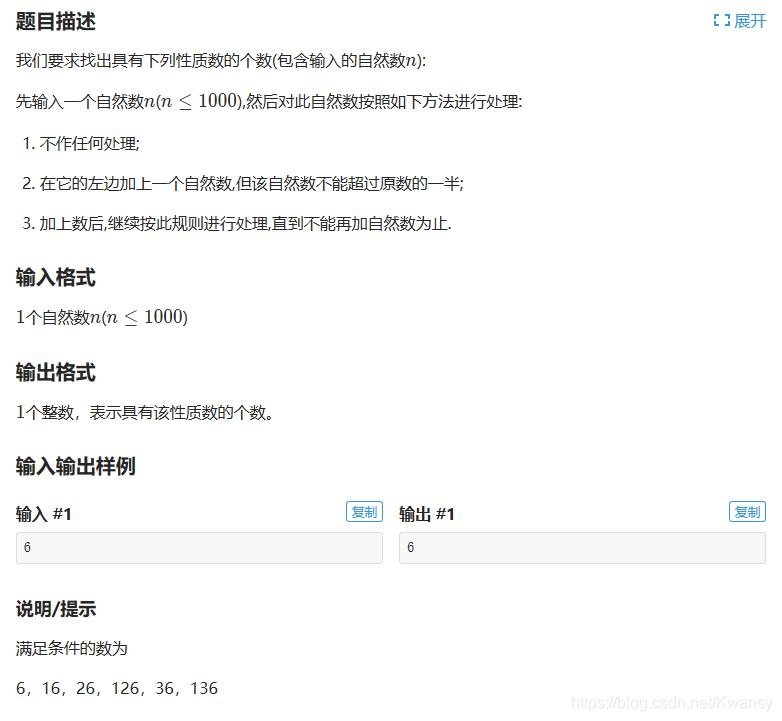在这里插入图片描述 题意：
给一个整数n(n≤1000），在n左边添加一个不大于n/2的数构成一个新数，然后对添加的数也做相同处理。统计所有可能性。
以10举例，可以有以下14种可能性：

110
210,1210,
310,1310,
410,1410,2410,12410,
510,1510,2510,12510,
10

解法一（递归）：
理解了题意之后，不难写出递归的解法：

#include <bits/stdc++.h>
using namespace std;
int n,cnt=1;
int A[1005];
void dfs(int x){
	for(int i=1;i<=x/2;i++){
		cnt++;
		dfs(i);
	}
}
int main(){
	cin >> n;
	dfs(n);
	cout << cnt;
}

输出：

这个解法可以得出正确答案，但是数据大了会超时。接下来主要有两种做法，一种是用递归把1000种答案算出来，把答案写在代码里，根据输入来输出答案，时间复杂度是O(1)，这样做的好处是不需要动脑，实在找不到规律就只能用这个笨办法了，题目数据是1000，所以花个几十分钟还是可以算出来的；第二种办法是小范围的打印出前几项答案，找规律，改用递推公式解。
在这里插入图片描述找规律的代码：

#include <bits/stdc++.h>
using namespace std;
int n,cnt=1;
int A[1005];
void dfs(int x){
	for(int i=1;i<=x/2;i++){
		cnt++;
		dfs(i);
	}
}
int main(){
	for (int i = 0; i <= 50; i++) {
		cnt = 1;
		dfs(i);
		printf("%d:%d\n", i, cnt);
		A[i] = cnt;
	}
}

输出：

0:1
1:1
2:2
3:2
4:4
5:4
6:6
7:6
8:10
9:10
10:14
11:14
12:20
13:20
14:26
15:26
16:36
17:36
18:46
19:46
20:60
...

解法二（递推）：
根据以上结果，可以找出两条规律。
规律一：当n是奇数，A[i] = A[i-1]
规律二：当n是偶数，A[i] = A[i-1] + A[i/2]

因此答案如下：

#include <bits/stdc++.h>
using namespace std;
int A[1005]; // 记录答案
/* 根据题意算出前几项，以便找规律
  i     0 1 2 3 4 5 6 7  8  9 ...
  A[i]  1 1 2 2 4 4 6 6 10 10 ...
  规律一：当n是奇数，A[i] = A[i-1]
  规律二：当n是偶数，A[i] = A[i-1] + A[i/2]
*/
int main() {
	int n; cin >> n;
	A[0] = 1; A[1] = 1;
	for (int i = 2; i < 1000; i++) {
		if (i % 2 != 0) {
			A[i] = A[i-1];
		} else {
			A[i] = A[i-1] + A[i/2];
		}
	}
	cout << A[n];
    return 0;
}