[15]和有限的最长子序列和从前序与中序遍历序列构造二叉树-优快云博客

文章介绍了如何使用排序和二分查找算法找到数组中元素之和小于等于特定值的最长子序列的长度。此外，还讨论了从先序遍历和中序遍历序列构建二叉树的递归和迭代方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.和有限的最长子序列

题目要求

给你一个长度为 n 的整数数组 nums ，和一个长度为 m 的整数数组 queries 。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是 nums 中元素之和小于等于 queries[i] 的 子序列 的最大长度。

子序列 是由一个数组删除某些元素（也可以不删除）但不改变剩余元素顺序得到的一个数组。

示例 1：

输入：nums = [4,5,2,1], queries = [3,10,21]
输出：[2,3,4]
解释：queries 对应的 answer 如下：
- 子序列 [2,1] 的和小于或等于 3 。可以证明满足题目要求的子序列的最大长度是 2 ，所以 answer[0] = 2 。
- 子序列 [4,5,1] 的和小于或等于 10 。可以证明满足题目要求的子序列的最大长度是 3 ，所以 answer[1] = 3 。
- 子序列 [4,5,2,1] 的和小于或等于 21 。可以证明满足题目要求的子序列的最大长度是 4 ，所以 answer[2] = 4 。

思路

首先，我是一个弱智。

其次，这个题虽然给出了子序列的定义，但是这道题要求返回的并不是子序列，而是子序列的最大长度，所以具体子序列啥样的不用管。

所以可以直接排序数组之后来完成。

由题意可知，nums的元素次序对结果无影响，因此我们对 nums 从小到大进行排序。显然和有限的最长子序列由最小的前几个数组成。使用数组 f 保存 nums的前缀和，其中 f[i]表示前 iii 个元素之和（不包括 nums[i]）。遍历 queries，假设当前查询值为 q，使用二分查找获取满足 f[i]>q的最小的 i，那么和小于等于 q的最长子序列长度为 i−1。

class Solution:
    def answerQueries(self, nums: List[int], queries: List[int]) -> List[int]:
        f = list(accumulate(sorted(nums)))
        return [bisect_right(f, q) for q in queries]

顺带给出官方题解所用到函数的定义

itertools.accumulate(iterable[, func, *, initial=None])

创建一个迭代器，返回累积汇总值或其他双目运算函数的累积结果值（通过可选的 func 参数指定）。

如果提供了 func，它应当为带有两个参数的函数。输入 iterable 的元素可以是能被 func 接受为参数的任意类型。（例如，对于默认的加法运算，元素可以是任何可相加的类型包括 Decimal 或 Fraction。）

通常，输出的元素数量与输入的可迭代对象是一致的。但是，如果提供了关键字参数 initial，则累加会以 initial 值开始，这样输出就比输入的可迭代对象多一个元素。

bisect.bisect_right(a, x, lo=0, hi=len(a), *, key=None)

bisect.bisect(a, x, lo=0, hi=len(a), *, key=None)

类似于 bisect_left()，但是返回的插入点是 a 中已存在元素 x 的右侧。

返回的插入点 i 将数组 a 分成两半，使得左半边为 all(val <= x for val in a[lo : i]) 而右半边为 all(val > x for val in a[i : hi])。

key 指定带有单个参数的 key function 用来从数组的每个元素中提取比较键。为了支持搜索复杂记录，键函数不会被应用到 x 值。

如果 key 为 None，则将直接进行元素比较而不需要中间的函数调用。

2.从前序与中序遍历序列构造二叉树

题目要求

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

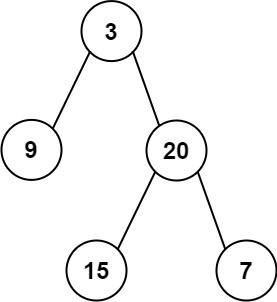
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

思路

。。。

官方分别给出了递归和迭代两种思路。

递归

只要我们在中序遍历中定位到根节点，那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的，因此我们就可以对应到前序遍历的结果中，对上述形式中的所有左右括号进行定位。

这样以来，我们就知道了左子树的前序遍历和中序遍历结果，以及右子树的前序遍历和中序遍历结果，我们就可以递归地对构造出左子树和右子树，再将这两颗子树接到根节点的左右位置。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        #递归
        def getTree(preorderLeft,preorderRight,inorderLeft,inorderRight):
            if preorderLeft > preorderRight:
                return None
            root = TreeNode(preorder[preorderLeft])
            inorderRoot = inorder.index(root.val)
            sizeOfLeft = inorderRoot - inorderLeft

            root.left = getTree(preorderLeft+1,preorderLeft+sizeOfLeft,inorderLeft,inorderRoot-1)
            root.right = getTree(preorderLeft+sizeOfLeft+1,preorderRight,inorderRoot+1,inorderRight)
            return root
        n = len(preorder)
        return getTree(0,n-1,0,n-1)

迭代

对于前序遍历中的任意两个连续节点 u 和 v，根据前序遍历的流程，我们可以知道 u 和 v 只有两种可能的关系：

v 是 u 的左儿子。这是因为在遍历到 u 之后，下一个遍历的节点就是 u 的左儿子，即 v；

u 没有左儿子，并且 v 是 u 的某个祖先节点（或者 u 本身）的右儿子。如果 u 没有左儿子，那么下一个遍历的节点就是 u 的右儿子。如果 u 没有右儿子，我们就会向上回溯，直到遇到第一个有右儿子（且 u 不在它的右儿子的子树中）的节点 ua，那么 v 就是 ua的右儿子。

我们归纳出上述例子中的算法流程：

我们用一个栈和一个指针辅助进行二叉树的构造。初始时栈中存放了根节点（前序遍历的第一个节点），指针指向中序遍历的第一个节点；

我们依次枚举前序遍历中除了第一个节点以外的每个节点。如果 index 恰好指向栈顶节点，那么我们不断地弹出栈顶节点并向右移动 index，并将当前节点作为最后一个弹出的节点的右儿子；如果 index 和栈顶节点不同，我们将当前节点作为栈顶节点的左儿子；

无论是哪一种情况，我们最后都将当前的节点入栈。

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        #迭代
        if not preorder:
            return None
        root = TreeNode(preorder[0])
        nodeStack = [root]
        inorderIndex = 0
        for i in range(1,len(preorder)):
            preorderVal = preorder[i]
            node =nodeStack[-1]
            if node.val == inorder[inorderIndex]:
                while nodeStack and nodeStack[-1].val == inorder[inorderIndex]:
                    node = nodeStack.pop()
                    inorderIndex += 1
                node.right = TreeNode(preorderVal)
                nodeStack.append(node.right)
            else:
                node.left = TreeNode(preorderVal)
                nodeStack.append(node.left)
        return root