数据结构 树【重建二叉树】

一、题目描述

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

例如输入前序遍历序列{1,2,4,7,3,5,6,8}

和中序遍历序列{4,7,2,1,5,3,8,6}，

则重建二叉树并返回。

输入

[1,2,3,4,5,6,7],[3,2,4,1,6,5,7]

返回值

{1,2,5,3,4,6,7}

 

二、思路 

本题思路是递归思想。

首先分析根结点，将这棵树分成根+左+右的结构，

再依次将其左子树和右子树按照上述方式进行递归，直至某结点的左右子树为空。

那么此时这个结点也就是叶子结点了。

下图中，

pre:先序遍历

vin:中序遍历

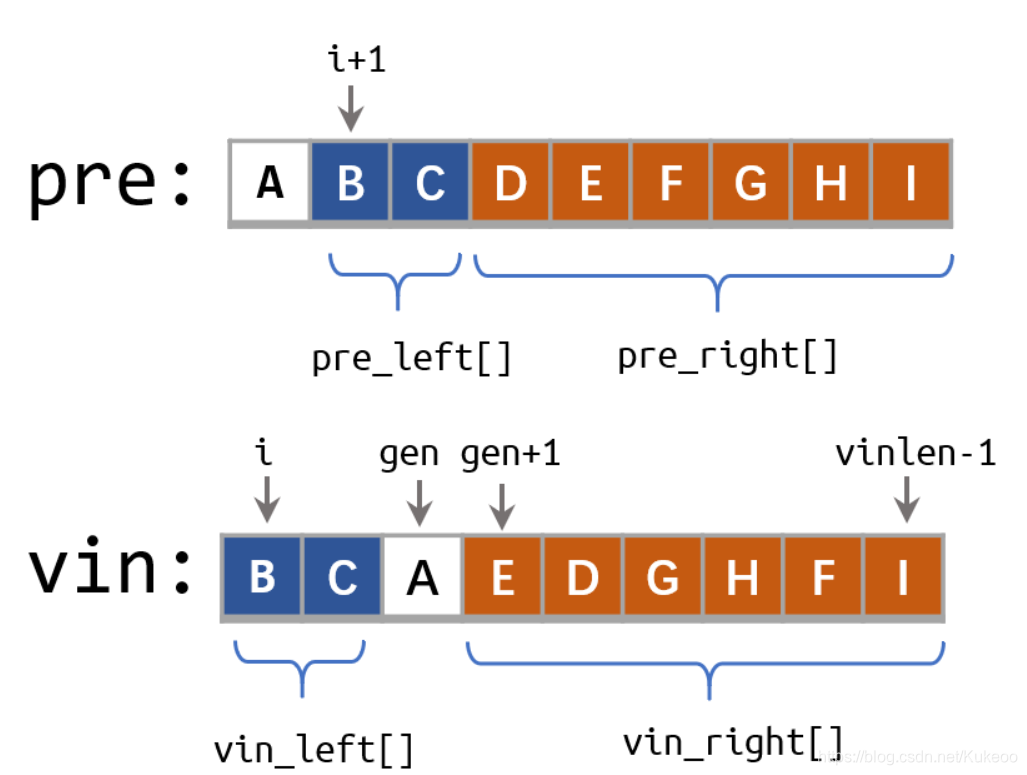
每次构造四个容器：

先序遍历的左子树容器pre_left[]

先序遍历的右子树容器pre_right[]

中序遍历的左子树容器vin_left[]

中序遍历的右子树容器vin_right[]

然后：

1. 由先序序列第一个pre[0]在中序序列中找到根节点位置gen
2. 以gen为中心遍历
   • 0~gen左子树
     • 子中序序列：0~gen-1，放入vin_left[]
     • 子先序序列：1~gen放入pre_left[]，+1可以看图，因为头部有根节点
   • gen+1~vinlen为右子树
     • 子中序序列：gen+1 ~ vinlen-1放入vin_right[]
     • 子先序序列：gen+1 ~ vinlen-1放入pre_right[]
3. 由先序序列pre[0]创建根节点
4. 连接左子树，按照左子树子序列递归（pre_left[]和vin_left[]）
5. 连接右子树，按照右子树子序列递归（pre_right[]和vin_right[]）
6. 返回根节点

 

三、代码

Tree rebuild(vector<Tree> pre, vector<Tree> vin)
{
	//如果容器大小为0，则返回空，无需继续遍历
	int vinlen = vin.size();
	if (vinlen == 0)
	{
		return NULL;
	}
	//创建四个子容器
	vector<Tree> pre_left, pre_right, vin_left, vin_right;
	//创建根结点，注意，这里的根结点只是本次遍历的根结点，
	//如果是首轮，则是整棵树的根结点；
	//如果不是首轮，则是子树的根结点。
	Node* head = (Node*)malloc(sizeof(Node));
	//初始化根结点
	head->data = pre[0]->data;
	int rootLocation = 0;
	//开始寻找根结点
	for (int i = 0; i < vinlen; i++) 
	{
		if (vin[i]->data == pre[0]->data)
		{
			rootLocation = i;
			break;
		}
	}

	//开始将建立左子树的前序遍历与中序遍历
	for (int i = 0; i < rootLocation; i++)
	{
		//中序最后一个是根结点
		Node* n = (Node*)malloc(sizeof(Node));
		n = vin[i];
		vin_left.push_back(vin[i]);
		//先序第一个为根节点
		pre_left.push_back(pre[i + 1]);
	}
	//同样的方法：右子树
	for (int i = rootLocation + 1; i < vinlen; i++) {
		vin_right.push_back(vin[i]);
		pre_right.push_back(pre[i]);
	}
	head->left = rebuild(pre_left, vin_left);
	head->right = rebuild(pre_right, vin_right);
	return head;
}

四、测试

int main()
{
	vector<Tree> pre;
	vector<Tree> vin;
	int pre_x = 7;
	while (pre_x)
	{
		int x;
		cin >> x;
		Node* p = (Node*)malloc(sizeof(Node));
		p->data = x;
		p->left = NULL;
		p->right = NULL;
		pre.push_back(p);
		pre_x--;
	}
	int vin_x = 7;
	while (vin_x)
	{
		int x;
		cin >> x;
		Node* p = (Node*)malloc(sizeof(Node));
		p->data = x;
		p->left = NULL;
		p->right = NULL;
		vin.push_back(p);
		vin_x--;
	}
	Tree t = rebuild(pre, vin);
	levelOrder(t);
	releaseTree(t);
	return 0;
}

 

运行截图：