前言:
递归是一个很强大和奇妙的方法,在计算机当中递归算法很强大的算法,它可以使解决问题的方法变得相当简单,递归是通过递归函数实现的,计算机通过不停的调用递归函数,使得问题分解成小型的问题,而这些问题又和递归函数相同,使得代码变得优雅和简洁。
递归分类
递归在分类分为基本递归和尾递归
- 基本递归:
基本递归是一种强大的方法,如果一个问题可以通过调用自身来得以解决,那么这个问题就带有递归的特性,那么程序员便可以使用递归函数通过在这个函数中调用自身解决问题。 - 尾递归:
递归的一种方式,由于这种特殊的递归在编译器中会进行代码的优化,所以可以在利用递归的有点(简单优雅)的同时,大大减少递归带来的不足(空间利用率低下)。
为了区别这两种递归的不同:
我们举一个求 n! 的例子分别使用基本递归和尾递归的方式进行代码的分析。开始之前我们先分析阶乘的公式:
F
(
n
)
=
n
!
=
n
(
n
−
1
)
(
n
−
2
)
⋯
(
1
)
F(n)=n!=n (n-1)(n-2)\cdots(1)
F(n)=n!=n(n−1)(n−2)⋯(1)
对这个公式进行优化可以看为
F
(
n
)
=
n
∗
F
(
n
−
1
)
n
>
1
F(n)=n*F(n-1) \qquad\qquad n>1
F(n)=n∗F(n−1)n>1
最后公式化成基本递归的形式是:
F
(
n
)
=
{
1
如
果
n
=
0
,
n
=
1
F
(
n
)
=
n
∗
F
(
n
−
1
)
,
n
>
1
n
∈
N
F(n)= \begin{cases}1\quad \ \ & 如果n = 0,n=1\\ F(n)=n*F(n-1), \quad \ \ & n>1 \quad n\in N \end{cases}
F(n)={1 F(n)=n∗F(n−1), 如果n=0,n=1n>1n∈N
求阶乘的基本递归代码的形式:
int fact1(int n)
{
if (n < 0)
{
return 0;
}
else if (n == 0)
{
return 1;
}
else if (n == 1)
{
return 1;
}
else
return n * fact1(n - 1);
}
在理解递归中的内存分配机制,我们先讨论一下内存的机制(有需要可以看看我之前的内存四区模型的文章 C语言内存四区的概念)简单的说就是系统在开辟一个内存给函数的时候,一般是在栈上开辟的。这个时候栈就分出一个 存储空间给这个函数使用。这个时候我们可以称这个这个存储空间为这个函数的栈帧,当这个函数运行的时候,这个栈帧就是活跃的或者存在的。当函数运行结束完成后,这个栈帧就死亡被系统自动释放,一个栈帧分为以下几个部分。
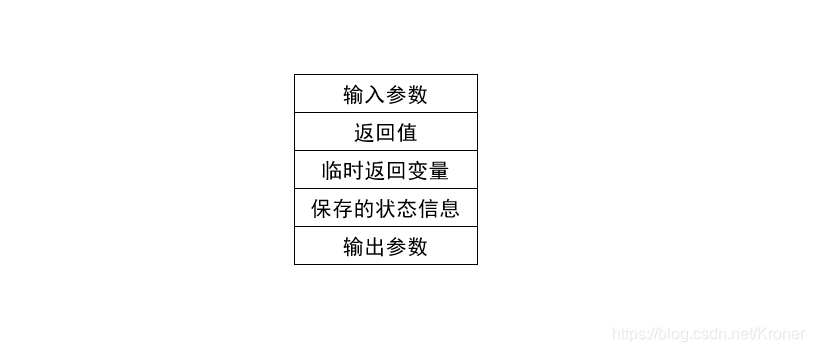
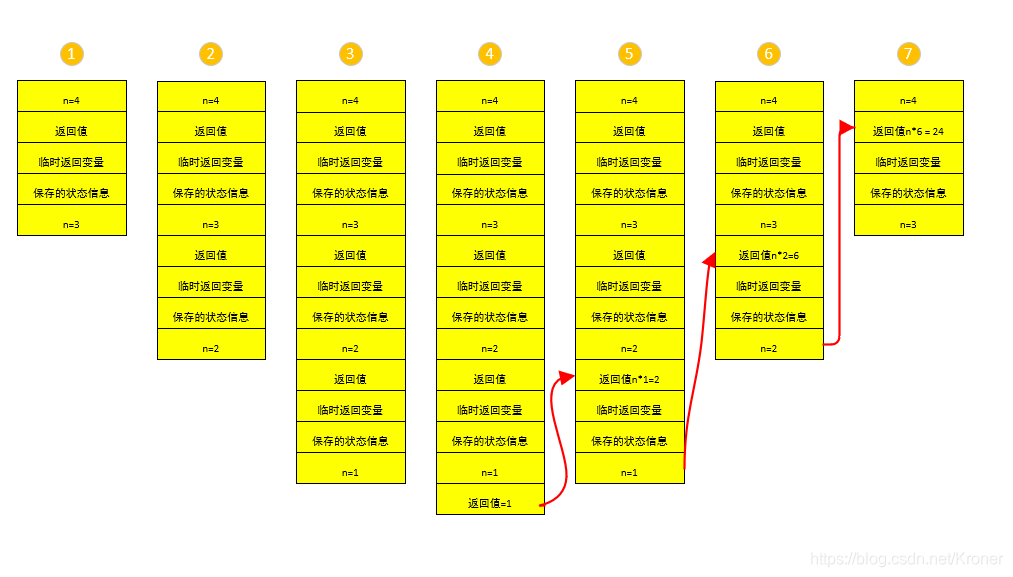
下面这副图简单的表示这个代码运行中的栈空间的运行情况:在n=4的时候,由于这个数值并没有满足函数的结束条件,所以这个时候编译器会接的开辟一个新的栈帧。将上一个函数的栈帧的输出参数n=3作为下一个栈帧的输入参数直到第四步,到第四步的时候满足递归的结束条件,于是返回值一步一步的返回,栈帧被一步一步的释放。
栈作为存储函数调用信息的存储结构是很好,因为栈是后进先出的特点,但是这也带来一些不足,只有当栈中信息完全没有作用的时候,这个栈帧才会被释放。这就说明,系统为维护栈帧必须占用相当大的内存,当数据很大的时候,相当大的内存的花销会造成系统的缓慢甚至崩溃,为了避免发生这种情况,我们就必须对基本的递归加以优化,使用迭代的方法将基本递归变成一种叫尾递归形式的递归方式。
同样为了了解尾递归的工作方式,我们同样选择同样的例子进行分析。将求n!的公式加以优化为尾递归的形式:
F
(
n
)
=
{
a
如
果
n
=
0
,
n
=
1
F
(
n
)
=
F
(
n
−
1
,
n
a
)
,
n
>
1
n
∈
N
F(n)= \begin{cases}a\quad \ \ & 如果n = 0,n=1\\ F(n)=F(n-1,na), \quad \ \ & n>1 \quad n\in N \end{cases}
F(n)={a F(n)=F(n−1,na), 如果n=0,n=1n>1n∈N
求阶乘的尾递归代码的形式:
int fact2(int n, int a)
{
if (n < 0)
{
return 0;
}
else if (n == 0)
{
return 1;
}
else if (n == 1)
{
return a;
}
else
return fact2(n - 1,n*a);
}
下面这张图是尾递归的栈运行中的过程图。因为对函数的单词递归的执行的最后一条语句也是递归,在执行最后一条语句后。编译器便会自动优化这段代码,因为新的栈帧和旧的栈帧是相同的迭代器结构,这不会改变函数的输出,但是却可以避免一次额外的函数调用,结果上提高了效率。
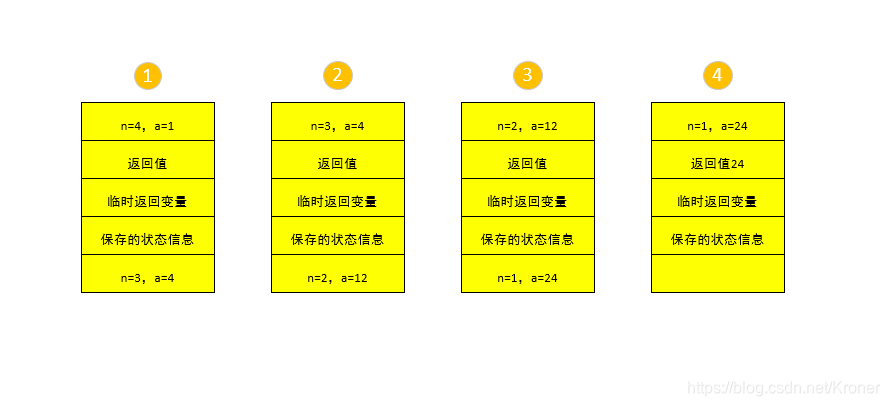





 本文介绍了计算机科学中的递归算法,包括递归的定义及其在解决问题时的优势。递归主要分为基本递归和尾递归。基本递归通过函数自身调用来解决问题,而尾递归则在编译器优化下能提高效率,减少空间消耗。通过求阶乘的例子,详细解析了两种递归的工作原理和内存分配机制。
本文介绍了计算机科学中的递归算法,包括递归的定义及其在解决问题时的优势。递归主要分为基本递归和尾递归。基本递归通过函数自身调用来解决问题,而尾递归则在编译器优化下能提高效率,减少空间消耗。通过求阶乘的例子,详细解析了两种递归的工作原理和内存分配机制。
















 1639
1639

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








