论文CLIP-EBC（基于CLIP的人群统计模型）详解

视频讲解

论文下载：https://arxiv.org/pdf/2403.09281v3.pdf

代码下载：https://github.com/Yiming-M/CLIP-EBC

论文Distribution Matching for Crowd Counting详解

论文Distribution Matching for Crowd Counting中人群统计损失（C Loss），最优化传输损失（OT Loss）以及总的变化损失（TV Loss）

 

        前面已讲过关于人群计数的几篇论文，在看本文论文之前希望大家先去看一下之前讲到的DMCount（Distribution Matching for Crowd Counting）和CLIP预训练对比语言模型，因为CLIP-EBC在损失函数方面使用到了DMCount提出的损失。CLIP-EBC并不是第一个将CLIP应用到人群计数领域的论文，前面还有一篇CrowdCLIP已经将CLIP应用到人群计数。不同是CLIP-EBC是基于全监督范式，而CrowdCLIP是基于Zero-shot范式。

目录

一 提出目的和方法

提出目的

提出方法

长尾分布问题

CLIP在人群计数中面临的挑战

贡献点

块级人群计数分布

二 整体模型架构

提升块级分类

离散化

标签纠正

损失函数设计

文本提示词设计

综合实验对比

块大小选择

消融实验

模型架构消融

可视化对比

总结

---

一 提出目的和方法

提出目的

        CLIP（对比语言-图像预训练）模型在识别任务（如零样本图像分类和目标检测）中展现出卓越性能，但其计数能力尚未得到充分研究——这源于将回归任务的计数转化为识别任务的内在挑战。本文重点探究CLIP在人群规模估计中的计数潜力。现有基于分类的人群计数方法存在离散化策略不当等问题，既阻碍了CLIP的应用，也导致性能欠佳。

提出方法

        提出增强型分块分类（EBC）框架。与传统方法不同，EBC采用整数值区间划分，有助于学习鲁棒的决策边界。在这一模型无关的EBC框架内，我们首次构建了完全基于CLIP的密度图生成模型CLIP-EBC。

长尾分布问题

        计数值呈现长尾分布的特性，导致高密度区域样本严重不足。针对这一挑战，部分研究通过将计数值分箱（归类）重构为分类任务，从而增加稀有值的样本量。与回归方法类似，这些基于分类的方法同样采用分块预测策略，但输出的是缩减空间尺寸的概率图——每个空间位置的向量表示各分箱的概率得分。推理阶段通过加权聚合各分箱均值生成密度图，最终积分获得预测计数。但这些方法存在若干导致性能不佳的缺陷：首先，与回归方法类似，它们对真实密度图进行高斯平滑预处理时面临核心问题——核宽度的选择。

        由于透视畸变导致图像中头部尺寸差异，理想情况应根据头部实际大小匹配核宽度，但计数任务通常不提供该信息，致使现有分类方法在标注中引入噪声而降低性能。其次，高斯平滑将离散计数值转换至连续空间[0,∞)，迫使采用实数区间分箱策略，这使得边界附近样本难以分类，模型无法学习最优决策边界。现有方法的另一局限是仅关注分类误差而忽视预测计数值与真值的接近程度，导致测试时可能出现分类误差相同但期望值不同的概率分布，从而影响性能表现。

CLIP在人群计数中面临的挑战

        (1) 专为识别设计的CLIP与回归性质的计数任务存在本质差异；

        (2) 现有基于分类的计数方法存在局限且效果欠佳。为此，本文聚焦人群计数任务，提出增强型分块分类(EBC)框架，专门解决当前分类方法的固有缺陷。通过最小化修改，现有回归方法可无缝融入EBC框架并获得显著性能提升

贡献点

提出创新的增强型分块分类（EBC）框架，从离散化策略、标签校正和损失函数三个维度显著改进了现有分类方法；

基于EBC框架，首次构建了完全基于CLIP的人群计数模型CLIP-EBC。该模型最大限度保留CLIP原始架构，不仅能够估计人群规模，还可生成精细的分布密度图；

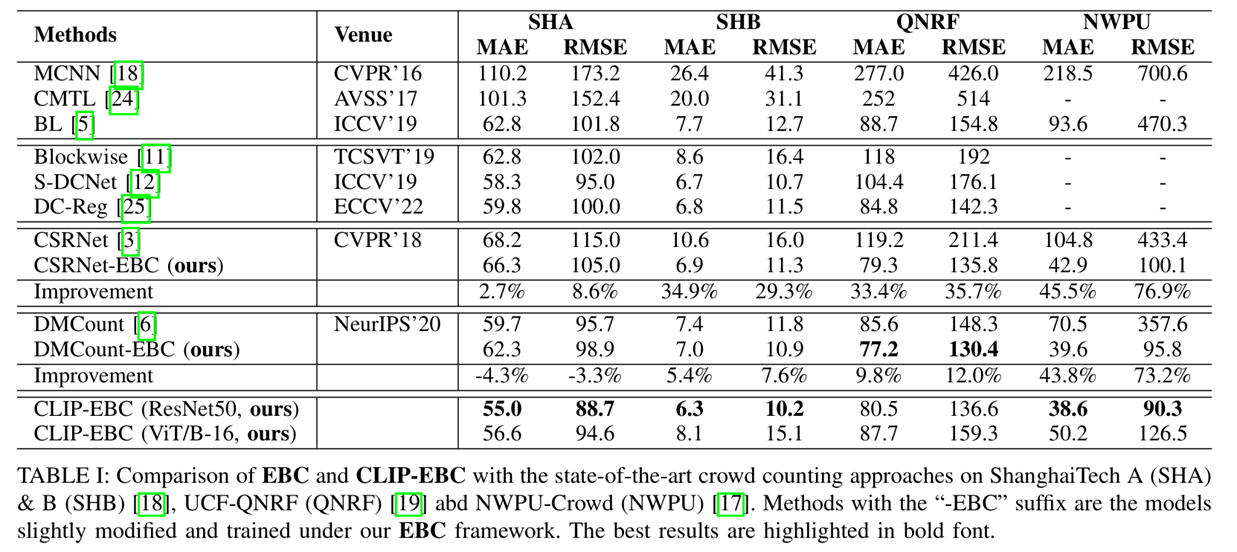
通过在多个数据集上的大量实验，验证了EBC框架对现有方法的提升效果（最高提升76.9%），同时证明CLIP-EBC作为最先进人群计数方法的卓越性能。

块级人群计数分布

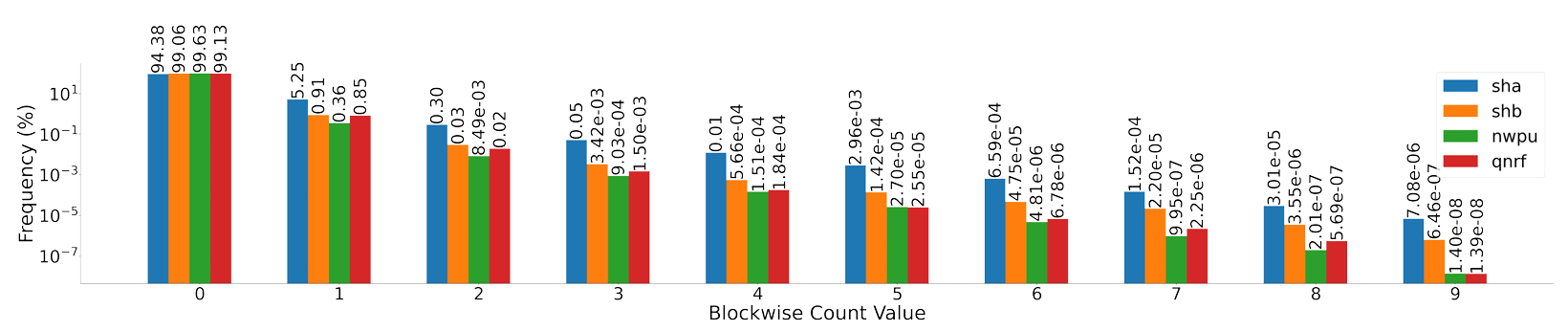
8×8块中人数分布。该块大小在许多论文中被广泛使用。所有数据集，即 ShanghaiTech A & B、NWPU-Crowd 和 UCF-QNRF，都表明0是主要值，而其他值严重欠采样。        

        有基于分类的方法旨在解决计数值长尾分布问题（如图所示），其中大数值区域样本严重不足，影响回归模型的性能。这些方法将取值范围[0, ∞)划分为互不重叠的区间以增加每类样本量，推理时通过加权各区间中点概率得分求和得到预测计数。DCNet采用相同分箱策略进行多尺度预测，但忽略了局部区域出现大数值概率较低的特性，反而加剧了类别不平衡。研究中提出的分块分类概念，模型输出概率图（每个像素的向量表示预测概率分布）。然而与回归方法类似，这些方法同样采用高斯核平滑真实密度图，导致两个关键问题：

（1）高斯平滑会引入标签噪声；

（2）平滑操作将离散整数计数值转换至连续实数空间，迫使采用临界相邻区间划分（如(0,0.5]和(0.5,1]），这种量化策略使边界附近样本难以分类。更重要的是，这些方法仅关注分类误差，却忽略了两个概率分布可能具有相同分类错误但期望值不同的情况，从而严重影响测试性能。

二 整体模型架构

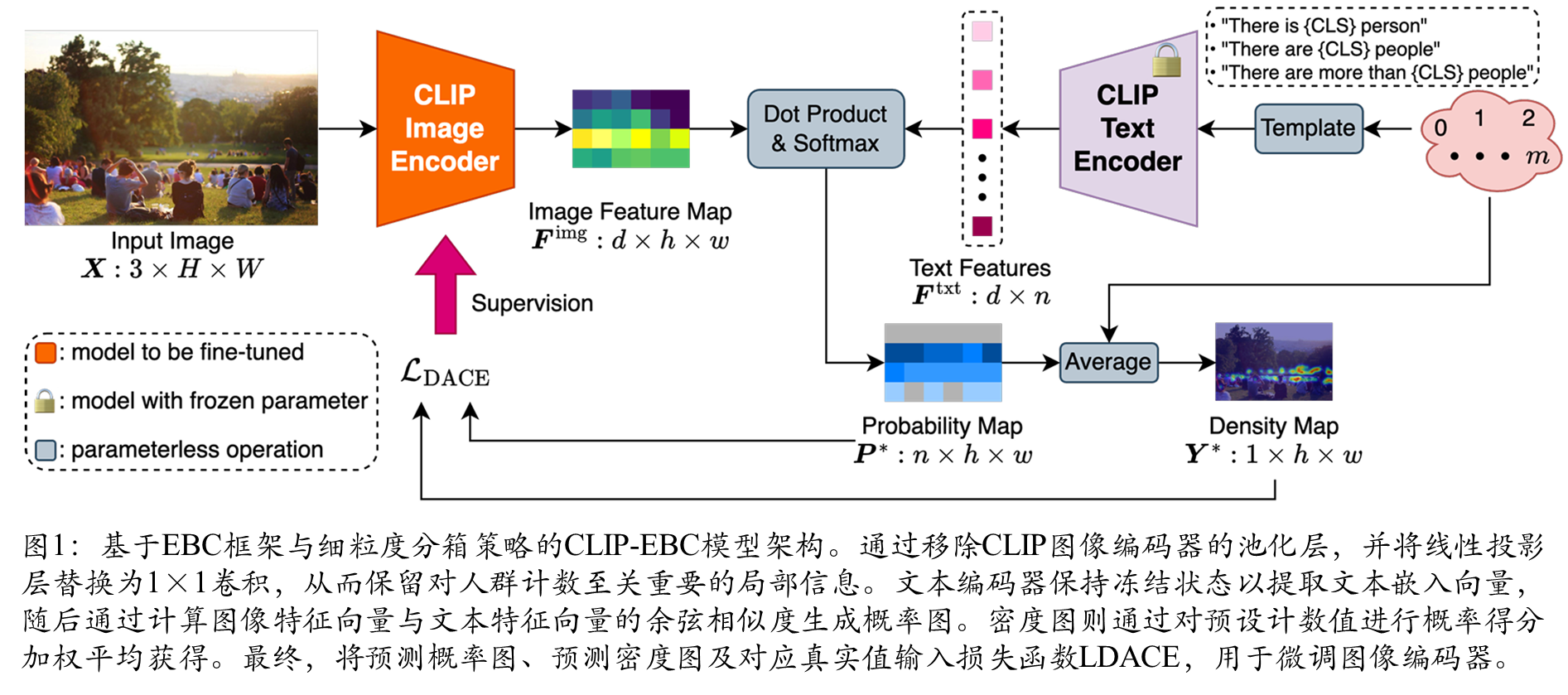
图像编码器架构​​

1. ​ ​特征提取模块​ ​

1. 移除 CLIP 原编码器的最终池化层和线性投影层

2. 保留骨干网络提取特征图 H ∈ ℝ^(c×(H//r)×(W//r))

1. c ：输出通道数（ ResNet 骨干）或嵌入维度（ ViT 骨干）

2. r ：缩减因子（ ResNet ）或分块尺寸（ ViT ）

2. ​ ​空间特征转换​ ​

1. 采用 1×1 卷积层替代多级投影层

2. 将 H 映射至 CLIP 嵌入空间，生成 F _ img ∈ ℝ^(d×(H//r)×(W//r))

​​与图4的对应关系​​

• 延续右图 EBC 框架的块预测机制

• 创新点：

• 细粒度分箱策略（每个整数独立分箱）

• CLIP 特征空间的直接利用率提升

• 通过 1×1 卷积实现空间维度保留

提升块级分类

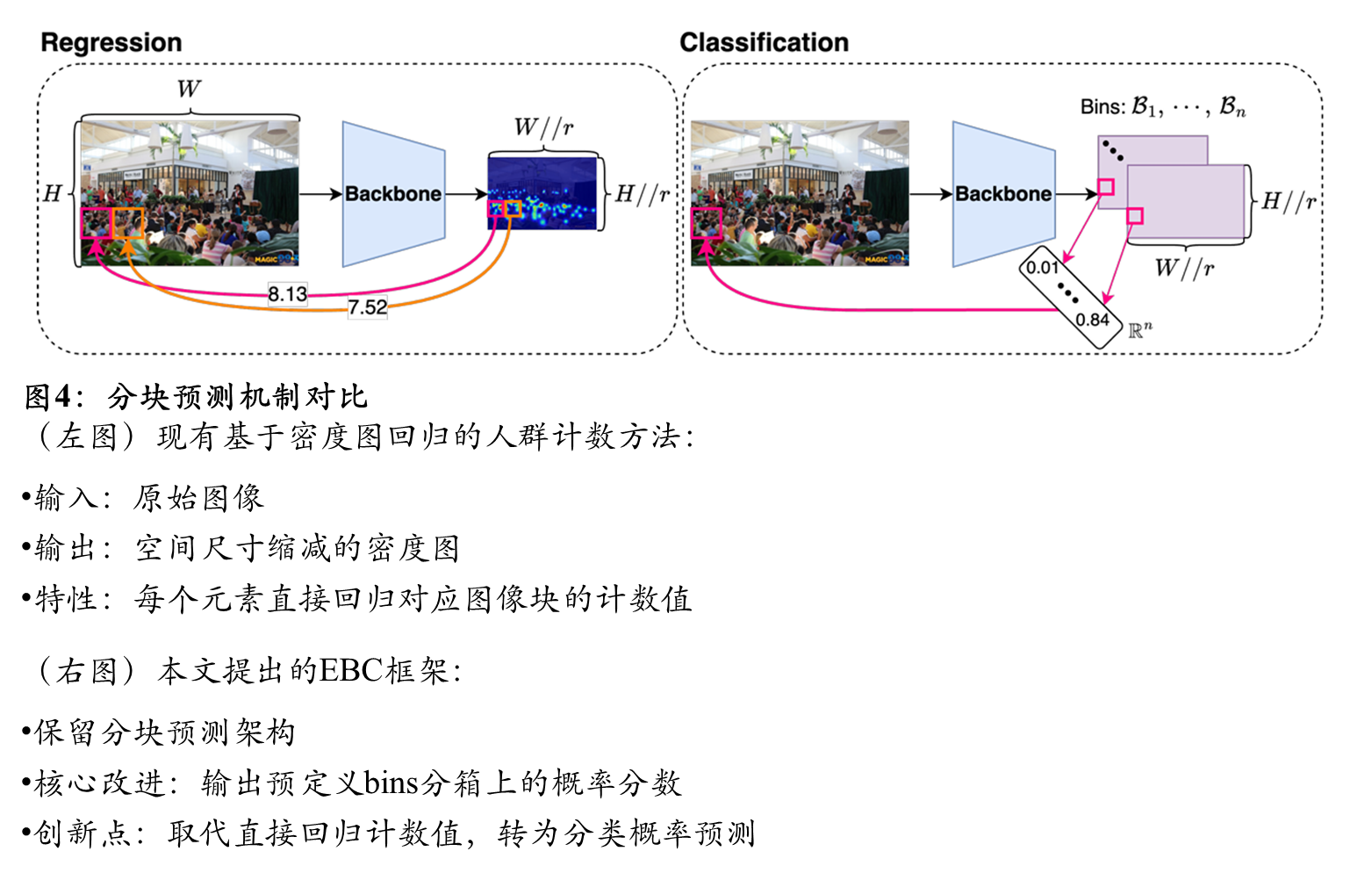
离散化

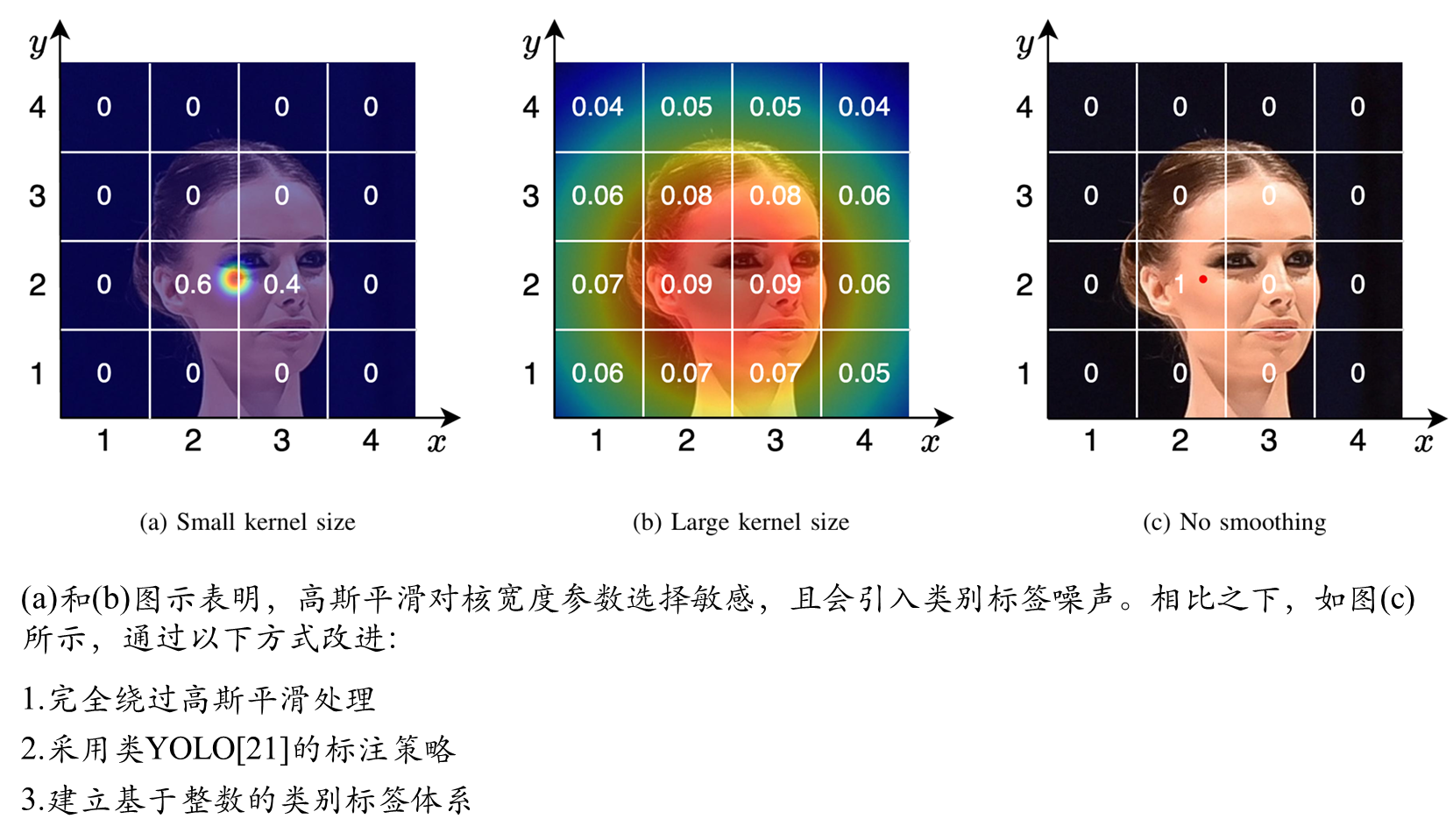
        先前基于回归的方法，现有的基于分类的方法使用高斯核对真实密度图进行平滑处理。这将support 集S⊂N转换为R+的子集。相应地，为了覆盖新的support 集，这些方法使用相邻区间作为分箱：{0}、(0,0.05]、(0.05,0.1]···。这种策略使得标签接近边界（例如0.05）的样本难以分类。此外，由于人群计数通常不提供头部尺寸，高斯平滑可能会在标签中引入额外噪声。如图3a和图3b所示，当核大小设置不当时，高斯平滑会产生错误的类别标签。为了解决这些问题，提出绕过高斯平滑并采用类似YOLO的方法（见图3c）：如果个体位于特定块内，强制仅该块预测该个体的存在，同时排除其他块进行此类预测。这种策略保留了计数的固有离散性。本文计数值support 集是S={0,1,···,m}，其中m表示最大允许计数值。本文提出了三种不同粒度的分箱策略：精细、动态和粗粒度。在精细级别，每个分箱仅包含一个整数；动态分箱策略创建不同大小的分箱；在粗粒度级别，每个分箱包含多个整数。

先前工作另一个缺点是它们使用每个区间的中点作为代表性计数值，这忽略了计数值不遵循均匀分布的事实。为了解决这个问题，建议使用每个分箱中的平均计数值作为代表点。

标签纠正

标签校正：现有方法均未解决高密度区域标注的核心难题——如图5所示，在64×64像素的洋红色标注框（坐标(646,301)）内，虽然标注人数为196人，但实际放大显示（图5c）可见：

        1. 因人群严重重叠导致个体位置难以辨识

        2. 低分辨率（源自 ShanghaiTech A 数据集的 IMG_120.jpg ）加剧标注误差

        3. 图像后处理（如尺寸调整）进一步引入噪声

现有方法均忽视了一个关键现实挑战——高密度区域的标注极易出现严重误差和噪声，导致与真实可观测的人数和位置存在显著偏差（如图所示）。该问题源于两个因素：

        1）低分辨率图像中标注者难以准确统计密集区域头部数量；

        2）标注后为了优化存储和训练时间进行的图像尺寸调整。此类错误会给人群计数模型传递错误的反向传播信号，严重损害实际性能。为此，提出将固定尺寸图像块中可观测人数的最大值约束为仅由块尺寸决定的小常数，具体设定最小可识别人体尺寸为s×s像素。因此，最大允许计数值m=(r //s )^2，如，当s=8时，图中包含区域的所有64 x 64块的最大允许计数值被限制为（64 // 8）^2 = 64，而不是195

损失函数设计

文本提示词设计

综合实验对比

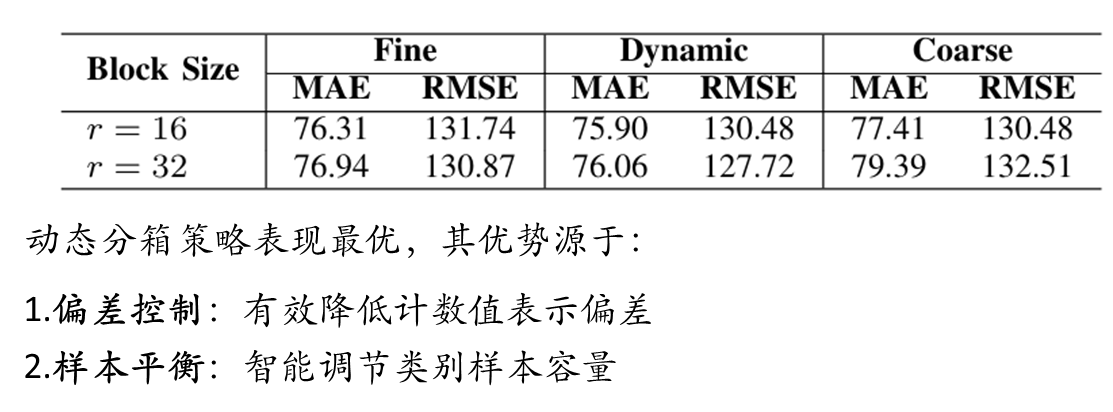
模型配置：为了与现有方法进行公平比较，主要关注块大小为 r=8。利用双线性插值来调整特征图的空间尺寸。设定最小可识别尺度为 s=4，因此每个块中的最大允许计数值为 m=(8//4)^2=4。该配置产生五个细粒度的bin：{0},{1},{2},{3},{4}。此外，还探索了另外两种块大小：r=16 和 r=32。 

 

1. ​ ​EBC 框架的普适性提升​ ​

1. 通过改造 CSRNet/DMCount 得到 CSRNet-EBC 和 DMCount-EBC

2. 在 NWPU 验证集上实现显著提升：

1. MAE 指标： CSRNet 提升 45.5% ， DMCount 提升 43.8%

2. RMSE 指标： CSRNet 提升 76.9% ， DMCount 提升 73.2%

2. ​ ​ CLIP-EBC 的竞争优势​ ​

1. 基于 ResNet 的 CLIP-EBC 创三项最佳记录：

1. ShanghaiTech A ： 55.0 MAE

2. ShanghaiTech B ： 6.3 MAE

3. NWPU ： 38.6 MAE

2. 证实 CLIP 原生架构在人群计数中的卓越潜力

块大小选择

消融实验

1. 分箱策略革新​ ​

1. 基线模型 Blockwise （ 连续区间分箱）： MAE 140.6

2. 改用整数分箱策略： MAE 降至 88.3 （提升 37.1% ）
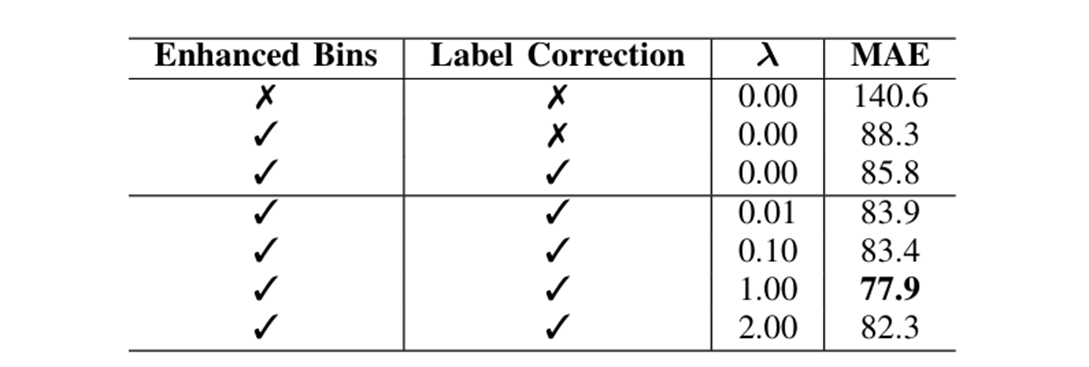
→ 验证离散化分箱能学习更优决策边界

2. ​ ​标签约束优化​ ​

1. 限制标签最大计数值： MAE 进一步降至 85.8

3. ​ ​损失权重影响​ ​

1. λ=0 （纯分类损失）：性能基准线

2. λ=1 （最优配置）： MAE 77.9

3. λ=2 ：模型泛化能力下降

模型架构消融

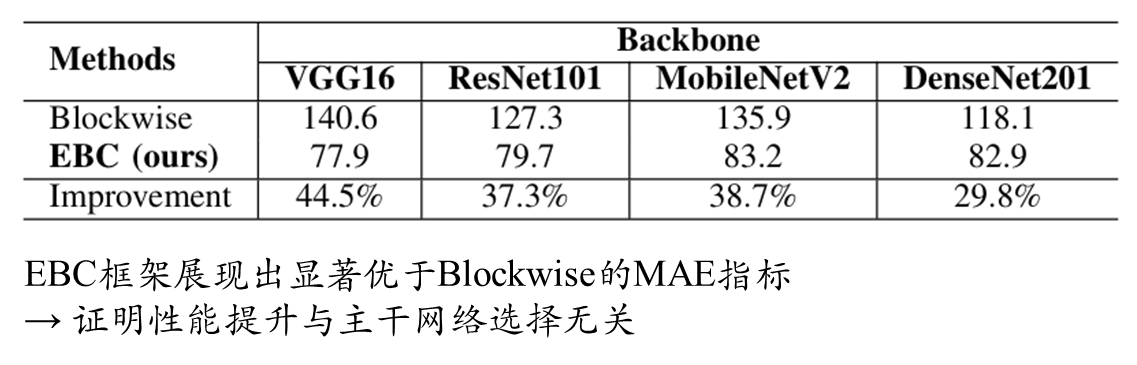
可视化对比

第一行​​：输入的人群图像
​​第二行​​：经高斯平滑处理的真实密度图
​​第三行​​：本方法CLIP-EBC（ResNet50）预测的密度图

​​场景分布​​

• 左侧三列：稀疏场景示例（来自 Part B ）

• 右侧三列：过度拥挤场景示例（来自 Part A ）

总结

社会影响声明	隐私风险： 与现有计数技术类似存在监控伦理问题； 实际部署可能引发 " 被计数 " 的心理不适。	数据偏差： 训练集偏见可能导致预测偏差； 或加剧特定人群的统计失衡现象。
技术局限	当前局限： 仅验证人类计数场景； 未充分挖掘 CLIP 多物体计数潜力。	发展路线： 后续研究将探索通用物体计数应用； 重点突破非人类对象的密度估计。