二叉树的基本性质

一、二叉树的定义：
二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。
如图所示为一颗二叉树：
​
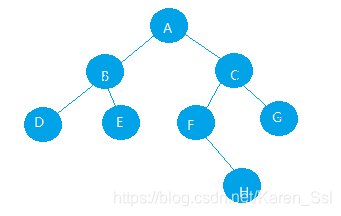
二、二叉树的基本性质：
1、子树不能相交
2、除了根节点外，每个结点有且仅有一个父节点
3、一颗N个结点的树有N-1条边

4、一个结点的子树的个数叫结点的度

5、在完全二叉树的情况下可以得到最多的叶子结点，叶子结点最多的个数与节点总数的奇偶数有关，奇数有（n-1）/2+1个，偶数个有n/2个

6、若规定根节点的层数为1，则一颗非空二叉树的第i层上最多有2的（i-1）次方个结点，其中i>0.
7、若规定只有根节点的二叉树的深度为1，则深度为K的二叉树的最大结点数是2^k - 1(k>=0)
8、对任何一颗二叉树，如果其叶结点个数为n0，度为2的非叶结点个数为n2，则有n0=n2+19、具有n个结点的完全二叉树的深度k为​上取整
10、对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有节点从0开始编号，则对于序号为i的节点有：
若i>0,双亲序号： (i-1)/2; i=0,则i为根节点编号，无双亲结点。
若2i+1<n,左孩子序号：2i+1，否则无左孩子
若2i+2<n,右孩子序号：2i+2，否则无右孩子

​