BP神经网络

BP(Back Propagation) 算法是神经网络深度学习中最重要的算法之一，了解BP算法可以让我们更理解神经网络深度学习模型训练的本质，属于内功修行的部分。

BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念，是一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最广泛的神经网络模型之一 。Minsky和Papert在颇具影响力的"perceptron" 一书中指出，简单的感知器只能求解线性问题，能够求解非线性问题的网络应该具有感知层，但是对隐藏层神经元的学习规则还没有合理的理论依据。

从前面介绍的感知器学习规则来看，其权值的调整取决于期望输出与实际输出之差：

但是对于各个隐藏层的节点来说，不存在已知的期望输出，因而该学习规则不能用于隐藏层的权值调整。

BP算法的基本思想是：学习过程由信号的正向传播和误差的反向传播两个过程组成。

正向传播时，把样本的特征从输入层进行输入，信号经过各个隐藏层的处理后，最后从输出层传出。对于网络的实际的输出与期望输出之间的误差，把误差信号从最后一层逐层反传，从而获得各个层的误差学习信号，然后再根据误差学习信号来修正各层神经元的权值。

这种信号正向传播与误差反向传播，然后各层调整权值的过程是周而复始地进行的。权值不断调整的过程，也就是网络学习训练的过程。进行此过程直到网络输出误差减小到预先设置的阈值以下，或者超过预先设置的最大训练次数。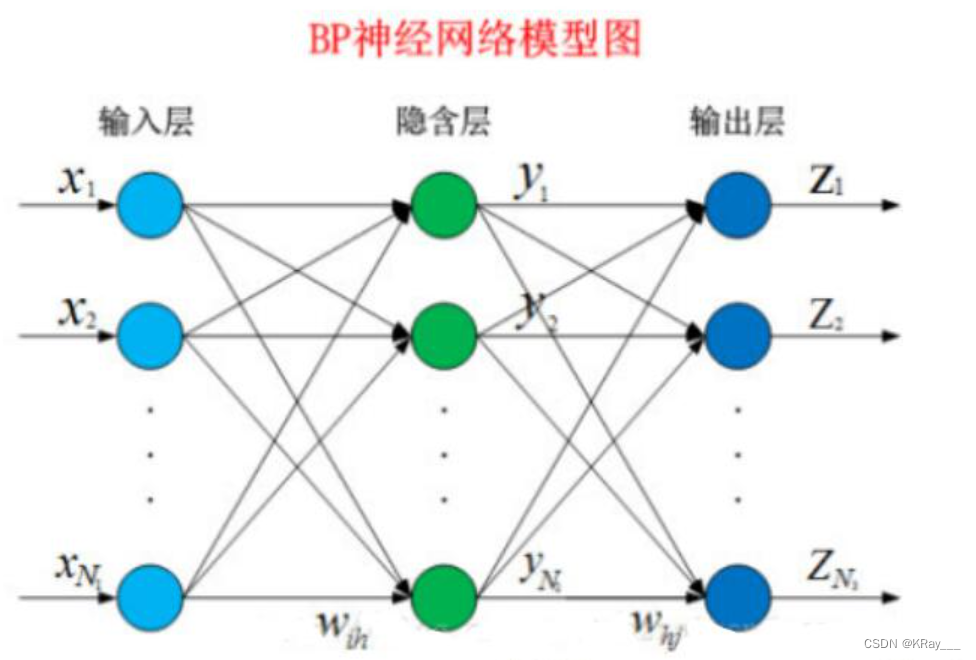

 已经知道在BP神经网络模型中，我们有三层结构，输入层、隐藏层、输出层,因此输入层到隐藏层的权值，设为,隐藏层第h个神经元的阈值我们设为。隐藏层到输出层的权值，设为​,输出层第j个神经元的阈值我们用表示。在下面这张图里，有输入神经元,个隐藏神经元，隐藏有个隐藏神经元阈值，个输出神经元，因此有个输出神经元阈值。

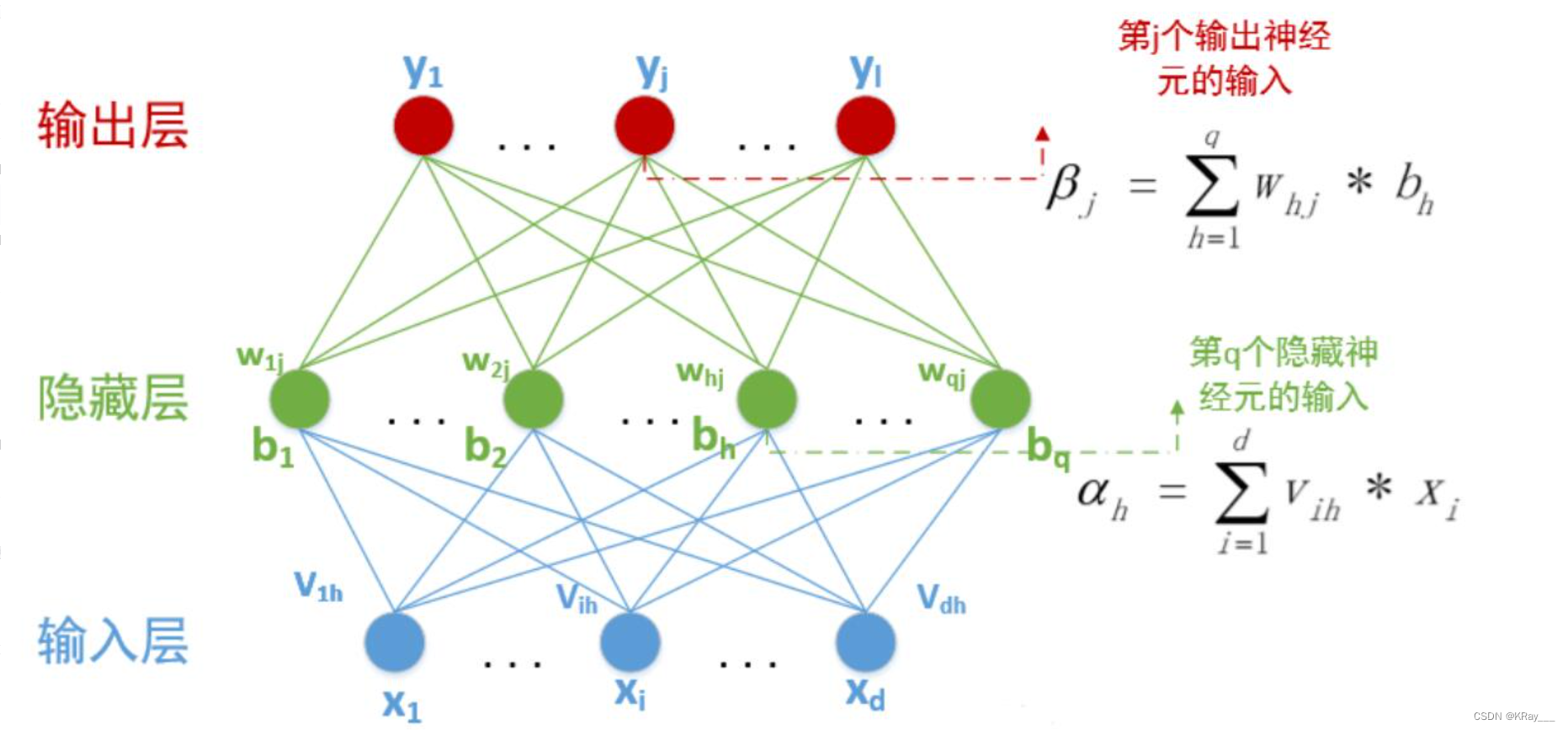
 对于第i个神经元，X1、X2、…、Xj为神经元的输入，输入常为对系统模型关键影响的自变量，W1、W2、…、Wj为连接权值调节各个输入量的占重比。将信号结合输入到神经元有多种方式，选取最便捷的线性加权求和可得neti神经元净输入:

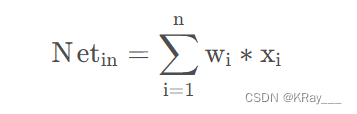
          θ \thetaθi表示该神经元的阈值，根据生物学中的知识，只有当神经元接收到的信息达到阈值是才会被激活。因此，我们将N e t i n Net 和θ j 进行比较，然后通过激活函数处理以产生神经元的输出。
  激活函数：激活函数这里我们不多重述。如果输出值有一定的范围约束，比如用来分类，一般我们用的最多的是Sigmod函数，它可以把输入从负无穷大到正无穷大的信号变换成0到1之间输出。如果没有约束的话，我们可以使用线性激活函数(即权值相乘之和)。这样我们得到的输出为：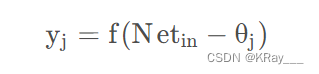

我们可以将公式化简一下，设第一个输入永远值为θ \thetaθ,权值为-1，则我们可以得到公式：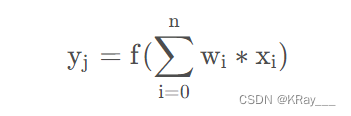

其中w0=-1,x0=θj,其中f为选择的激活函数。
  已经知道在BP神经网络模型中，我们有三层结构，输入层、隐藏层、输出层,因此输入层到隐藏层的权值，设为v i ,隐藏层第h个神经元的阈值我们设为γ h 隐藏层到输出层的权值，设为Whj 
 ,输出层第j个神经元的阈值我们用θj表示。在下面这张图里，有d输入神经元,q个隐藏神经元，隐藏有q个隐藏神经元阈值，1个输出神经元，因此有1个输出神经元阈值。