最近点对的定义:已知一系列的点对,需要找出最近的一对点。
在二维空间里,可用分治法求解最近点对问题。预处理:分别根据点的x轴和y轴坐标进行排序,得到X和Y,很显然此时X和Y中的点就是S中的点。
情况一: 点数小于等于三时
当只有两个点或者只有三个点的时候我们可以直接计算最近的两个点之间的距离。
情况二: 点数大于三时
首先把集合S分为两个集合分别表示为SL和SR,并且要保证集合SL中的的没一个点都必须位于集合SR的左边,还需要保证左右两集合的内的点数相同。然后在分别求出左右两边集合的的最近点对的距离DL和DR。令d=min(DL,DR)。如果S中的最近点对(P1,P2),P1,P2一个在SL中一个在SR中那么P1,P2一定在一L为中心的间隙内以L-d L+d 为边界,如下图所示:
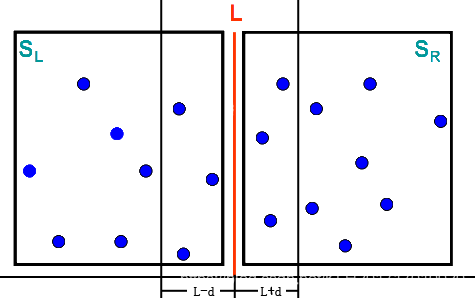
如果在SL中的点P和在SR中的点Q成为最近点对,那么P和Q的距离必定小于d。因此对间隙中的每一个点,在合并步骤中,只需要检验yp+d和yp-d内的点即可。
步骤1:根据点的y值和x值对S中的点排序。
步骤2:找出中线L将S划分为SL和SR
步骤3:将步骤2递归的应用解决SL和SR的最近点对问题,并令d=min(dL,dR)。
步骤4:将L-dL+d内的点以y值排序,对于每一个点(x1,y1)找出y值在y1-dy1+d内的所有点,计算距离为d’。 如果d’小于d,令d=d’,最后的d值就是答案。
如果此篇文章看懂以后可以去杭电OJ做一下1007这个题目,这个题目就是应用了这个思想可以练练手。







 本文详细解析了在二维空间中使用分治法求解最近点对问题的算法过程,包括预处理步骤、两种基本情况的处理,以及核心的分治递归策略。通过实例讲解,帮助读者理解并掌握该算法,最后推荐实践题目巩固学习。
本文详细解析了在二维空间中使用分治法求解最近点对问题的算法过程,包括预处理步骤、两种基本情况的处理,以及核心的分治递归策略。通过实例讲解,帮助读者理解并掌握该算法,最后推荐实践题目巩固学习。
















 1211
1211

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








