【HNU】数据结构-实验-图-多路径

原创已于 2025-06-03 17:03:06 修改 · 906 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #c++ #图论

于 2025-06-03 17:00:59 首次发布

大一下-数据结构专栏收录该内容

4 篇文章

订阅专栏

这是HNU数据结构课程的实验六，实际上来源于Codeforces 1547G，还是有一定难度的，让我们来看看这次的题目吧！

原题链接：1547G How Many Paths?

题目

【问题描述】

给定一个有向图 $G$ ，可以包含环，也可以有自环（节点连接到自身）,一对顶点之间最多有一条边相连。顶点编号从 $\sim n$ 。
从顶点 $u$ 到 $v$ 的路径是一个边的序列，描述如下：

顶点 $u$ 是路径上第一条边的开始顶点
顶点 $v$ 是路径上最后一条边的结束顶点
对于所有相邻边对，后一条边的开始顶点是前一条边的结束顶点

假定边的空序列是从 $u$ 到 $u$ 的路径。

对于每个顶点 $v$ ，输出以下四个值之一：

$0$ ，表示从顶点 $1$ 到 $v$ 没有路径
$1$ ，表示从顶点 $1$ 到 $v$ 只有一条路径
$2$ ，表示从顶点 $1$ 到 $v$ 有超过一条路径，且路径数是有限的
$- 1$ ，表示从顶点 $1$ 到 $v$ 有无穷多条路径

示例如下：

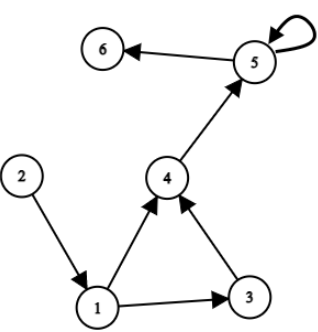
那么，

顶点 $1$ 的结果为 $1$ ：从 $1$ 到 $1$ 只有一条路径（路径长度为 $0$ ）
顶点 $2$ 的结果为 $0$ ：从 $1$ 到 $2$ 没有路径
顶点 $3$ 的结果为 $1$ ：从 $1$ 到 $3$ 仅有一条路径（为边 $(1, 3)$ ）
顶点 $4$ 的结果为 $2$ ：从 $1$ 到 $4$ 有超过一条路径，但路径数量是有限的（两条路径： $[(1, 3), (3, 4)]$ 和 $[(1, 4)]$ ）
顶点 $5$ 的结果为 $- 1$ ：从 $1$ 到 $5$ 的路径数是无穷的（环可以用于路径无穷多次）
顶点 $6$ 的结果为 $- 1$ ：从 $1$ 到 $6$ 的路径数是无穷的（环可以用于路径无穷多次）

【输入形式】

输入的第一行为一个整数 $\ (1 \leq t \leq 10^4)$ ，表示测试用例的组数，接下来是 $t$ 个测试用例，每个测试用例前有一个空行，这个空行的作用仅为阅读方便，有否不影响最终结果。

每个测试用例的第一行为两个整数 $n$ 和 $\ (1 \leq n \leq 4 \times 10^5, 1 \leq m \leq 4 \times 10^5)$ ，分别表示图的顶点数和边数。接下来的 $m$ 行包括了对边的描述，每行两个整数 $a_i$ 、 $b_i \ (1 \leq a_i, b_i \leq n)$ ，表示第 $i$ 边的开始点和结束点，图的顶点编号从 $1$ 至 $n$ ，给定的图中可以包含环（可能有 $a_i = b_i$ ）, 但不可以包含多边（即对于 $\neq j$ ，不可能有 $a_i = a_j$ 以及 $b_i = b_j$ ）。

所有测试用例中 $n$ 之和不超过 $\times 10^4$ ，同样的，所有的 $m$ 之和不超过 $\times 10^4$ 。

【输出形式】

输出包括 $t$ 行，第 $i$ 行是第 $i$ 个测试用例的答案，为一个 $n$ 个整数序列，取值在 $- 1$ 到 $2$ 之间。

【样例输入】

【样例输出】

1 0 1 2 -1 -1 
1 
-1 -1 -1 
1 0 0 0 0 
1 1 2 1

题目分析

看到这道题目首先容易想到的是强联通缩点+拓扑排序。

考虑从 $1$ 号顶点到某个顶点路径数为无穷的情况。若一个点处于顶点数大于 $1$ 的 $\mathrm{SCC}$ 中，并且顶点 $1$ 可到达此 $\mathrm{SCC}$ ，则到该点的路径数为无穷。因为来到此 $\mathrm{SCC}$ 后，其中的任意顶点互相可达，可以不断绕圈。另外，若一个点存在自旋边，则从顶点 $1$ 到该点的路径数显然也为无穷。

所以先使用 $\mathrm{Tarjan}$ 进行缩点，得到一个 $\mathrm{DAG}$ ，每个 $\mathrm{SCC}$ 内的点路径数显然是相同的。此时 $\mathrm{SCC}$ 序号恰为新 $\mathrm{DAG}$ 的拓扑序逆序，直接在新图上进行一次 $\mathrm{DP}$ 即可。

另外此题还有染色+多次 $\mathrm{DFS}$ 的官方解法，个人认为比较难想到。

代码

#include <bits/stdc++.h>
using namespace std;

template <typename T>
using vec2 = vector<vector<T>>;

vec2<int> G;
vector<int> low, num, scc_id, scc_size;
stack<int> dfs_s; //dfs栈
int dfn; //dfs序
int cnt; //强联通分量个数

void dfs(int u) {
    dfs_s.push(u);
    low[u] = num[u] = ++dfn;
    for (auto v : G[u]) {
        if (!num[v]) {
            dfs(v);
            low[u] = min(low[u], low[v]);
        } else {
            //处理回退边
            if (!scc_id[v]) {
                low[u] = min(low[u], num[v]);
            }
        }
    }
    if (low[u] == num[u]) {
        //u是scc祖先
        cnt++;
        int v;
        scc_size.push_back(0);
        do {
            v = dfs_s.top();
            dfs_s.pop();
            scc_id[v] = cnt;
            scc_size[cnt]++;
        } while (u != v);
    }
}

void Tarjan(int n) {
    cnt = dfn = 0;
    low = vector<int>(n + 1);
    num = vector<int>(n + 1);
    scc_id = vector<int>(n + 1);
    scc_size = vector<int>{0};

    for (int i = 1; i <= n; i++) {
        if (!num[i]) {
            dfs(i);
        }
    }
}

int main() {
    cin.tie(nullptr)->sync_with_stdio(false);

    int t;
    cin >> t;
    while (t--) {
        int n, m;
        cin >> n >> m;

        G = vec2<int>(n + 1, vector<int>());

        for (int i = 0; i < m; i++) {
            int u, v;
            cin >> u >> v;
            G[u].push_back(v);
        }

        Tarjan(n);

        vec2<int> G2(cnt + 1, vector<int>()); //scc缩点后的图
        vector<bool> self_loop(n + 1); //scc是否是单点自环
        for (int i = 1; i <= n; i++) {
            for (auto j : G[i]) {
                int u = scc_id[i], v = scc_id[j];
                if (u != v) {
                    G2[u].push_back(v);
                } else if (i == j) {
                    self_loop[u] = 1;
                }
            }
        }

        vector<int> dp(cnt + 1);
        int s = scc_id[1];
        //边界条件
        if (scc_size[s] > 1 || self_loop[s]) {
            dp[s] = -1;
        } else {
            dp[s] = 1;
        }

        //scc编号为逆拓扑序
        for (int u = cnt; u >= 1; u--) {
            //不可达的点对后续没有贡献
            if (dp[u] == 0) continue;
            for (auto v : G2[u]) {
                //状态转移
                if (dp[u] == -1 || scc_size[v] > 1 || self_loop[v]) {
                    dp[v] = -1;
                } else if (dp[v] != -1) {
                    dp[v] = min(dp[v] + dp[u], 2);
                }
            }
        }

        for (int i = 1; i <= n; i++) {
            cout << dp[scc_id[i]] << " \n"[i == n];
        }
    }


    return 0;
}