1 实验图
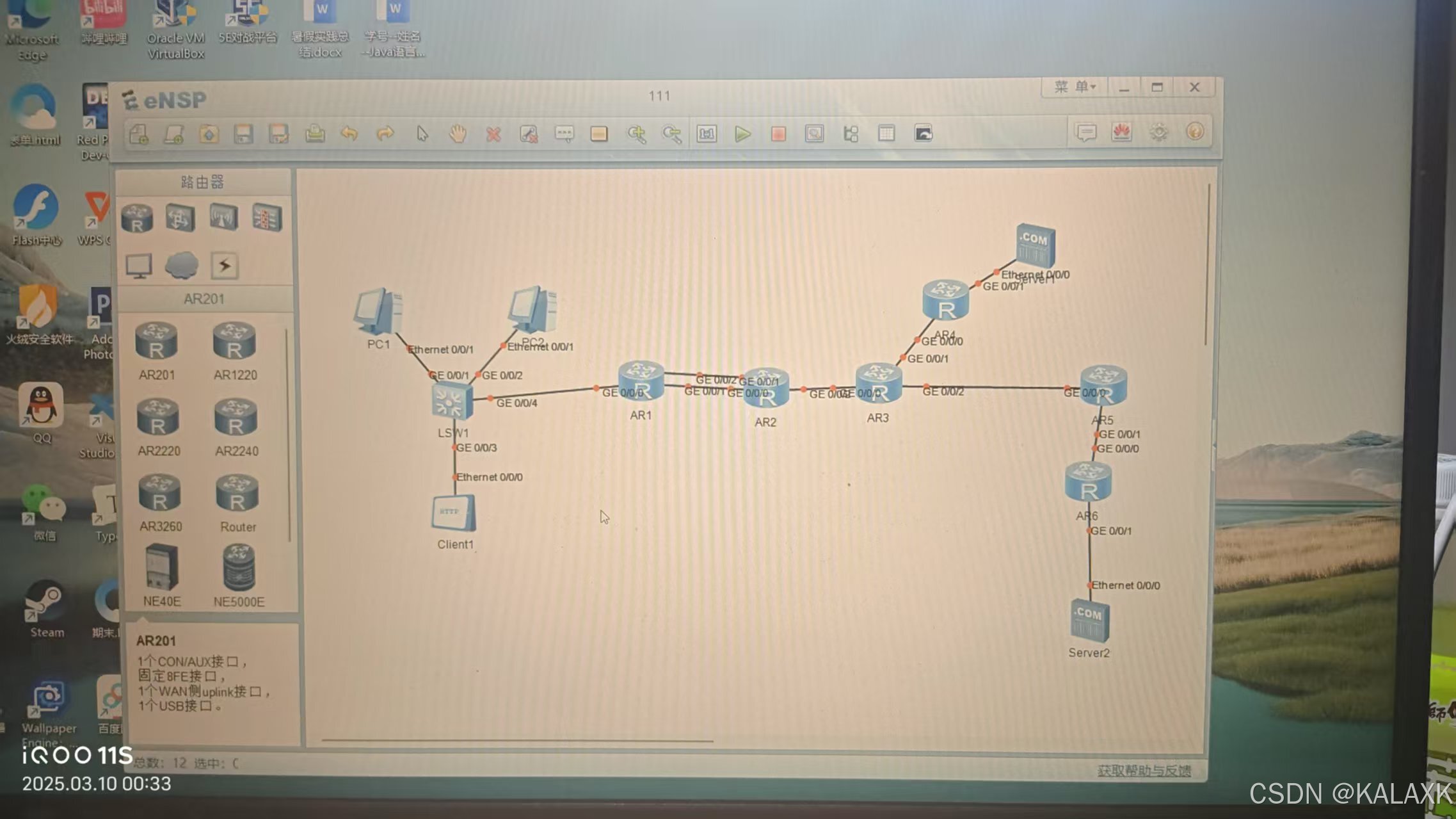 2 实验过程
2 实验过程
对各个路由器民命对学校网络进行基于192.168.1.0/24的子网划分,对运营商、百度网络进行基于3/3/3/0/24的子网划分,后期为满足要求,将采取配置ACL以允许PC1访问3.3.3.0/24网段,
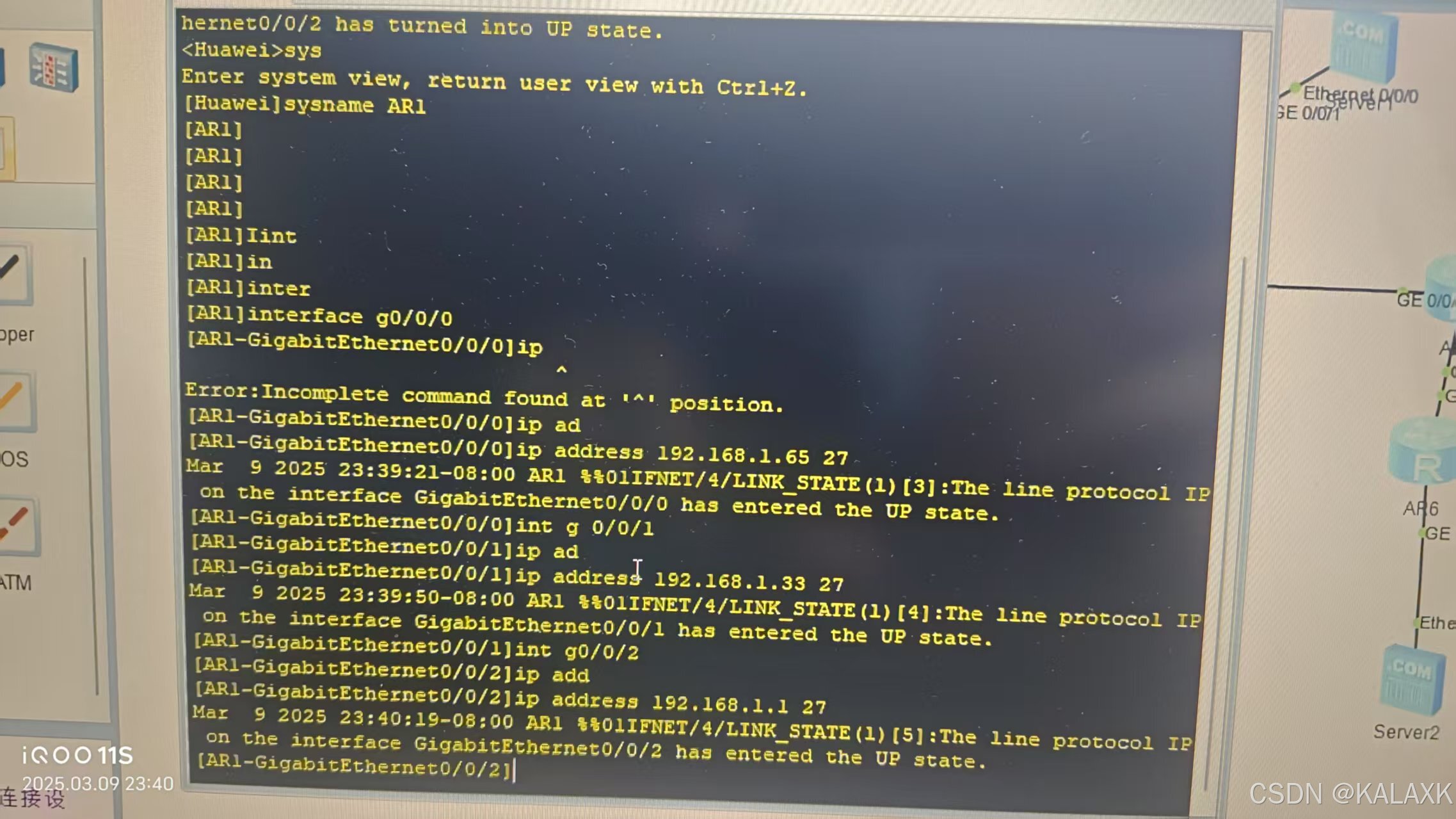
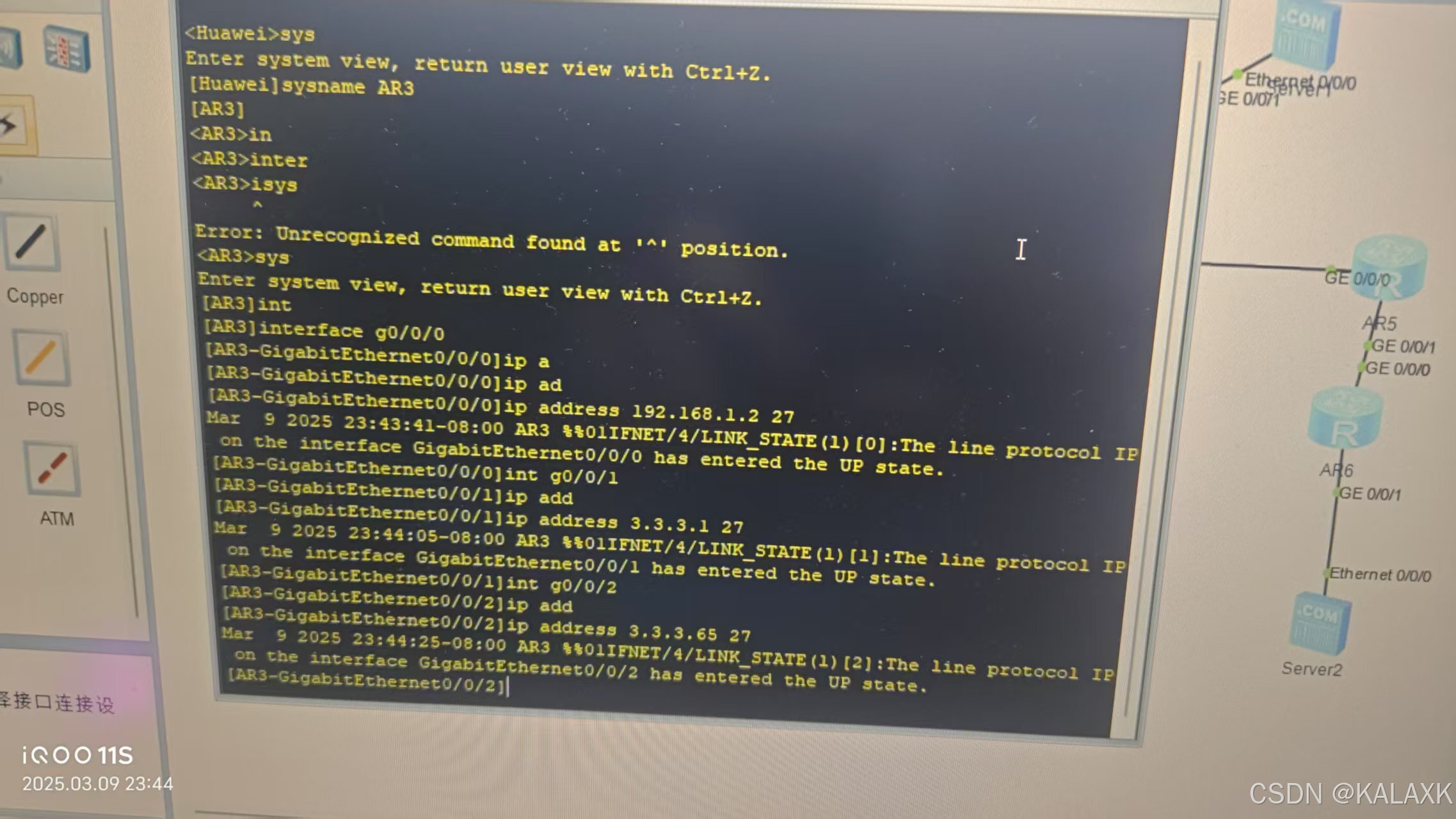
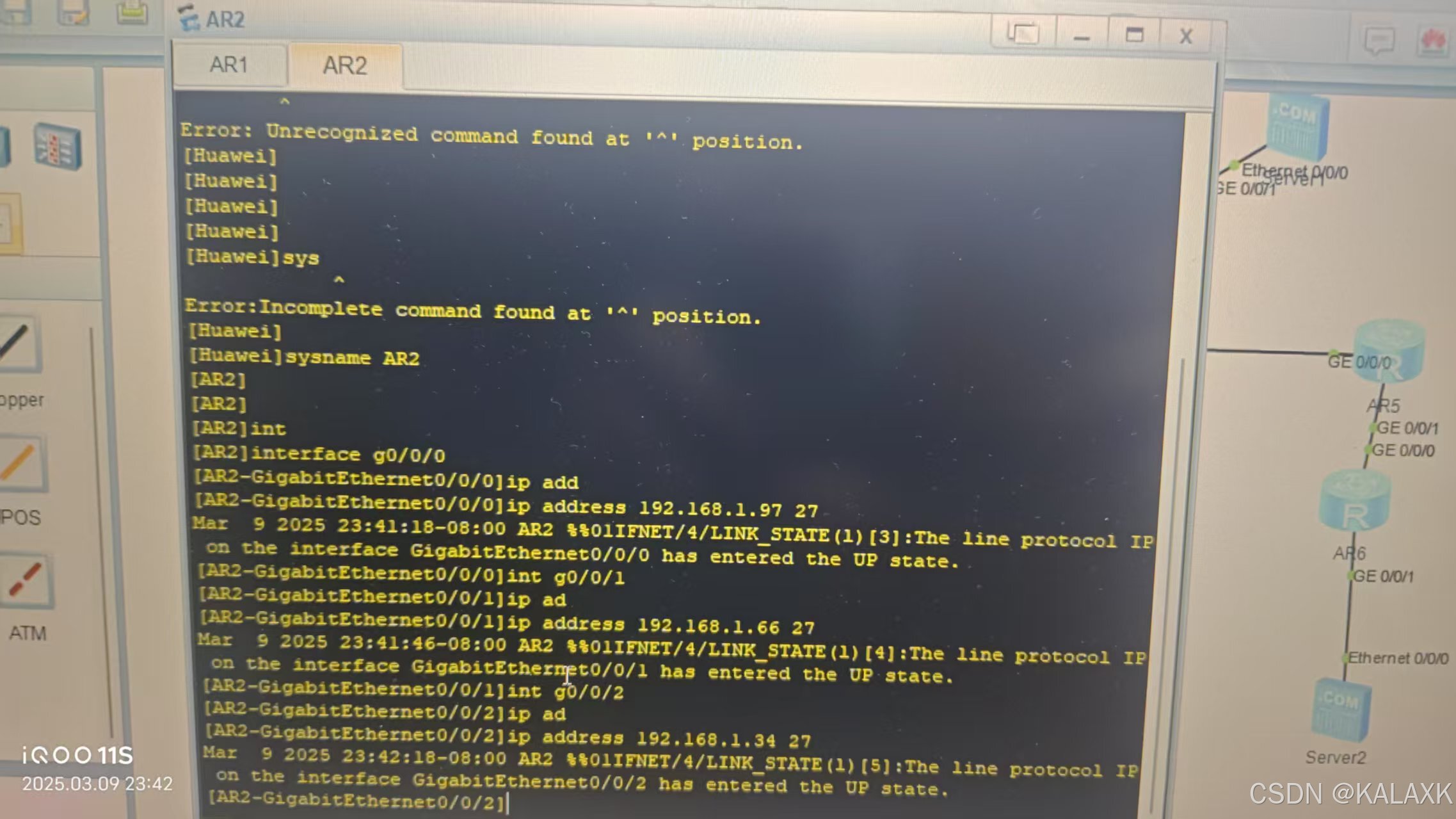
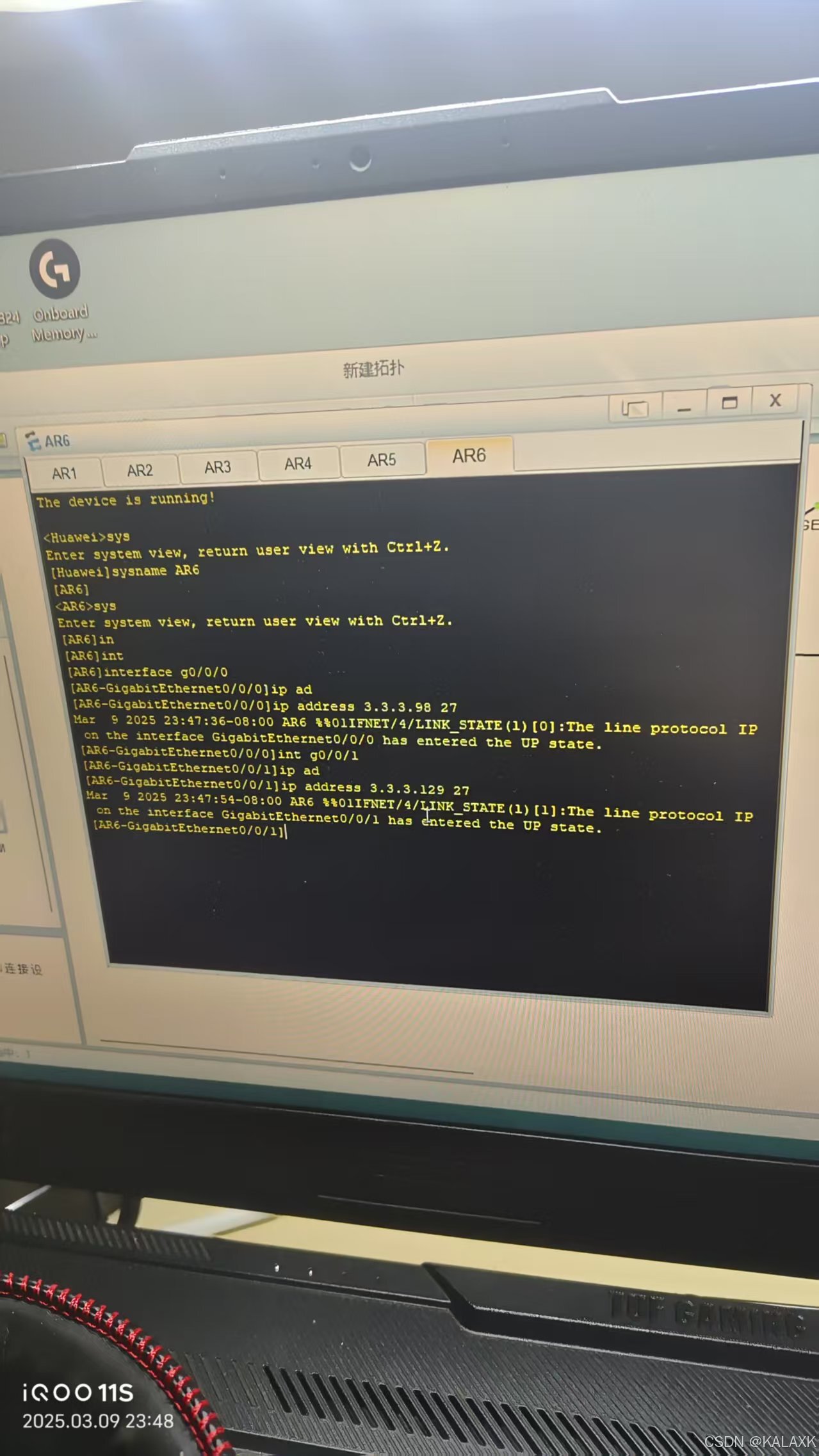
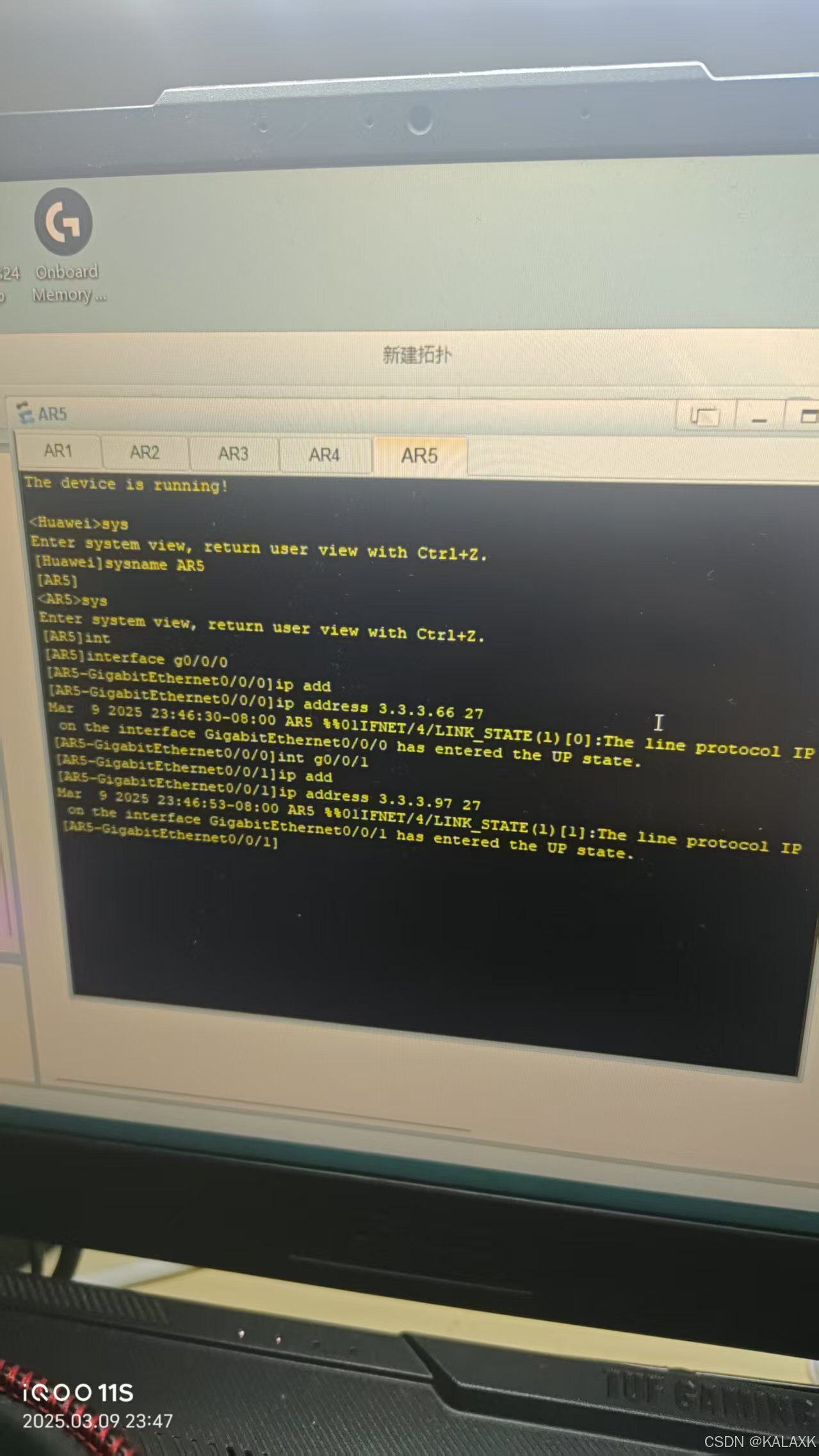
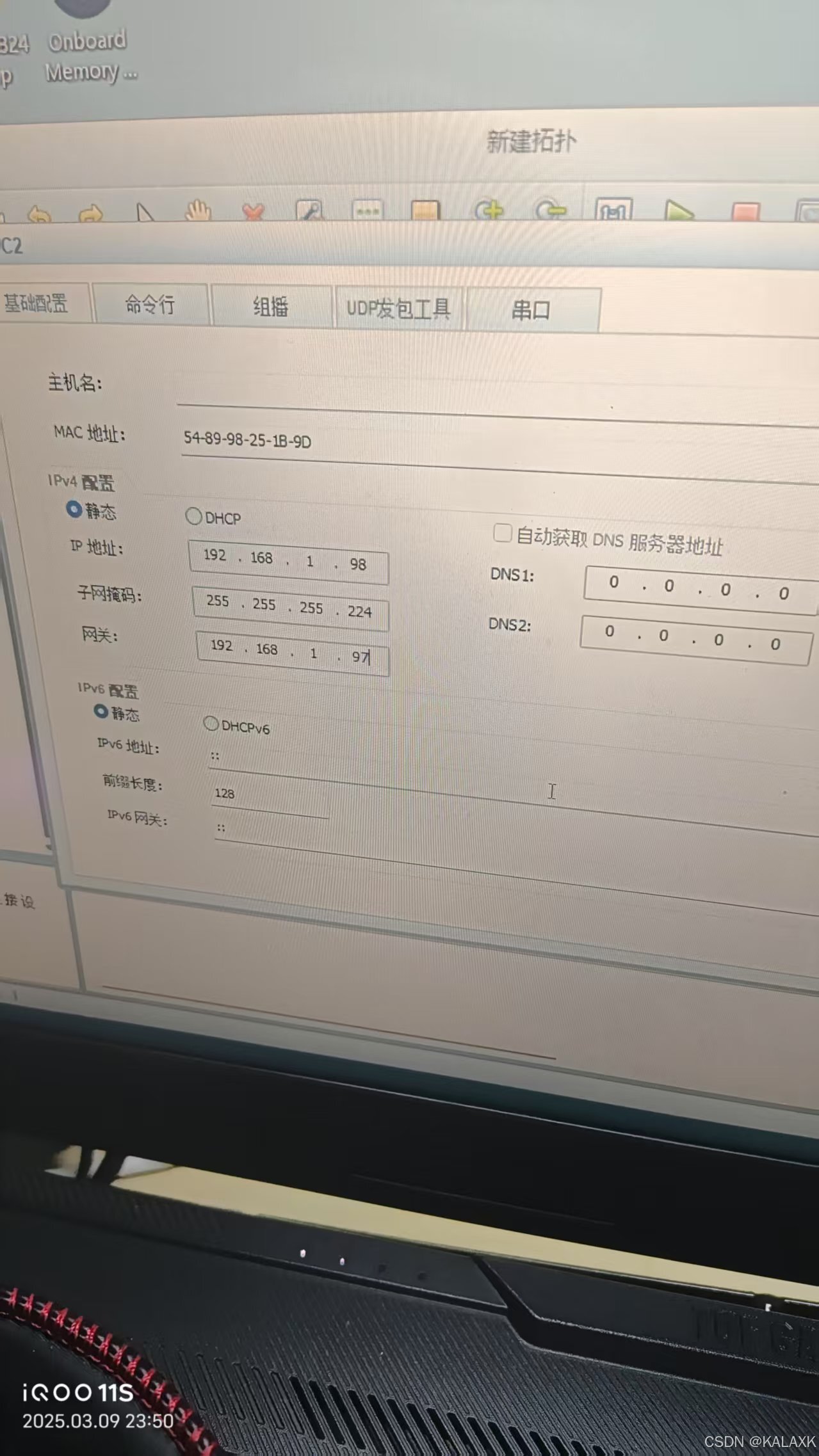
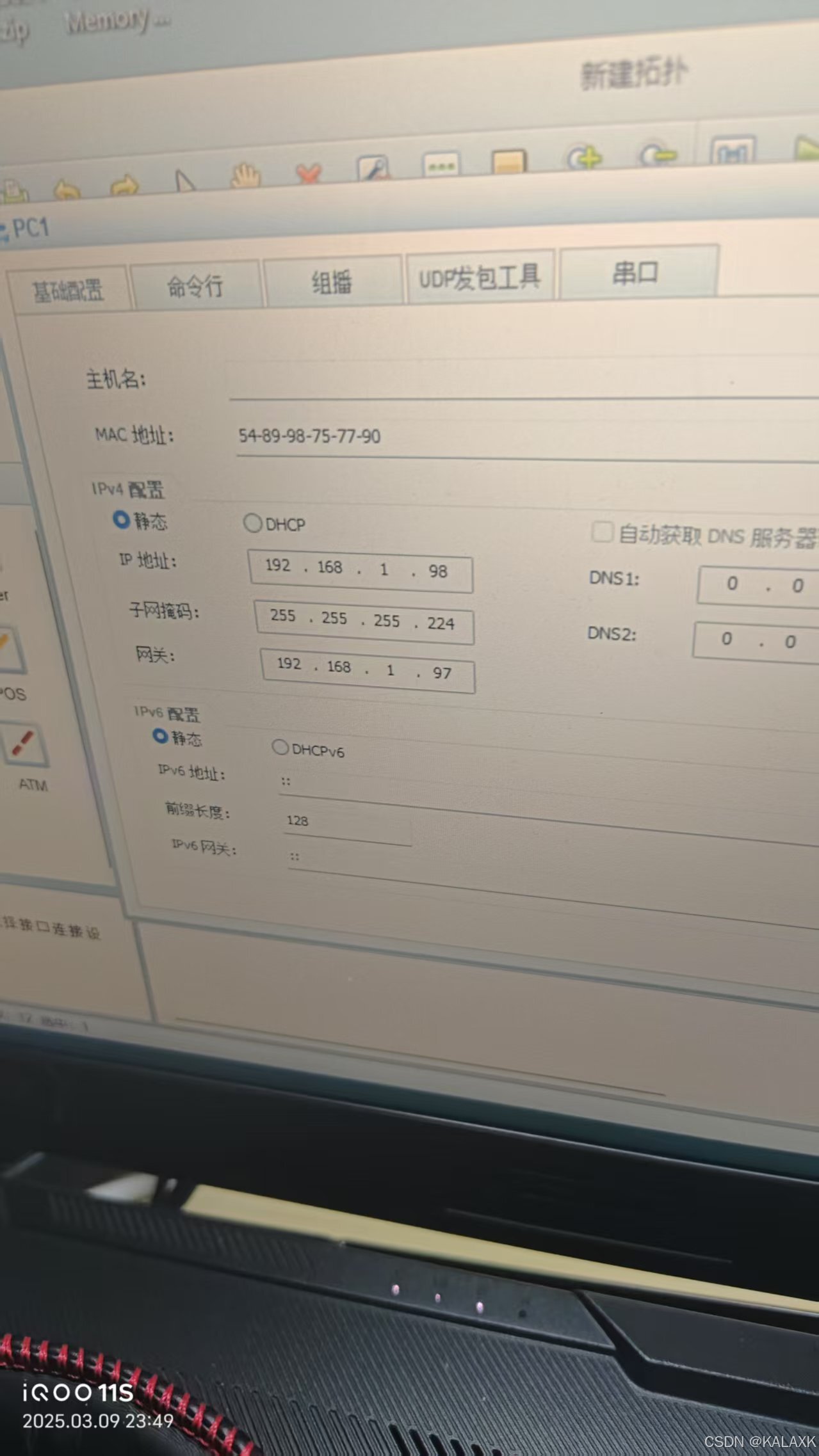 2 配置静态路由
2 配置静态路由
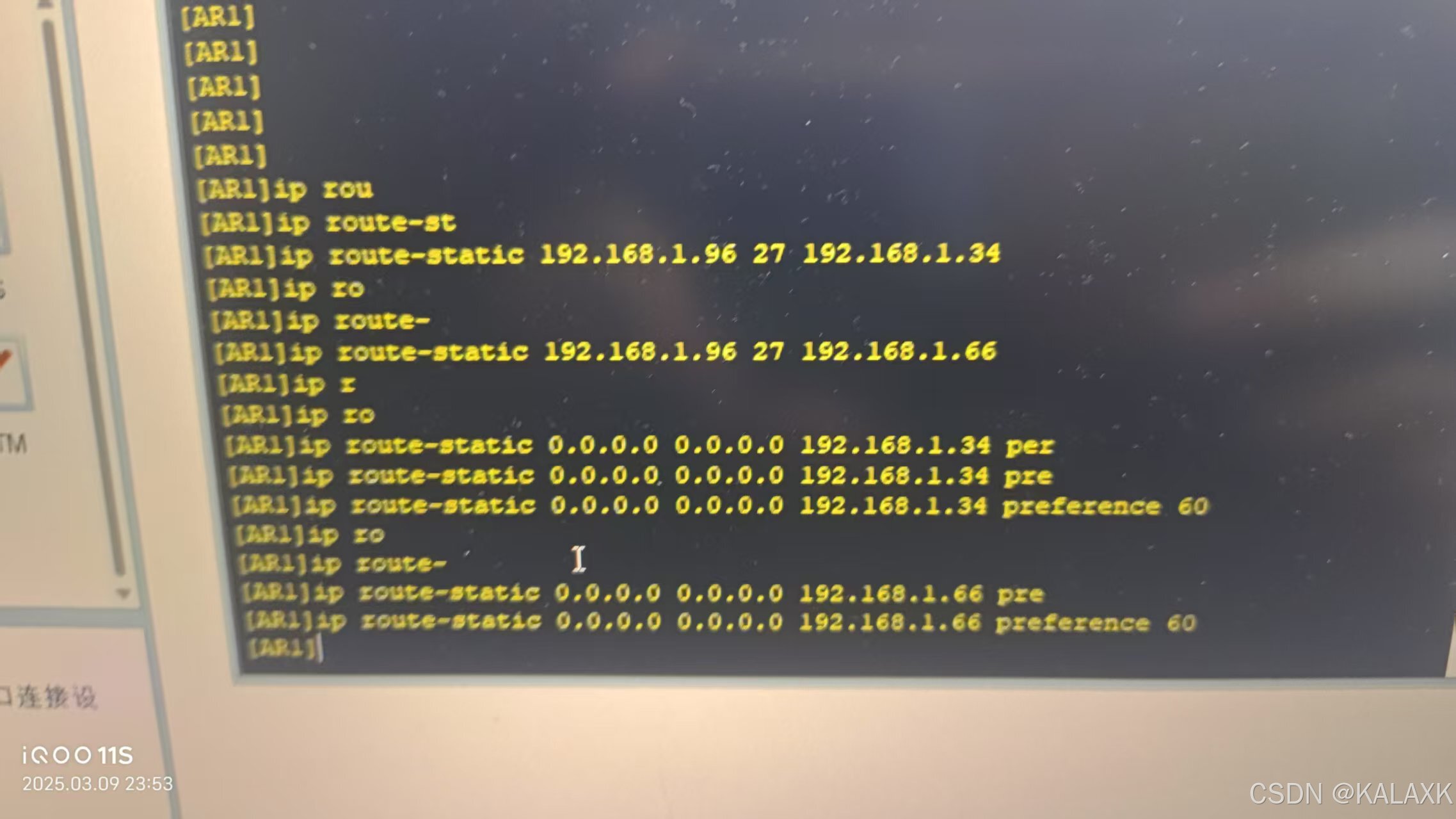
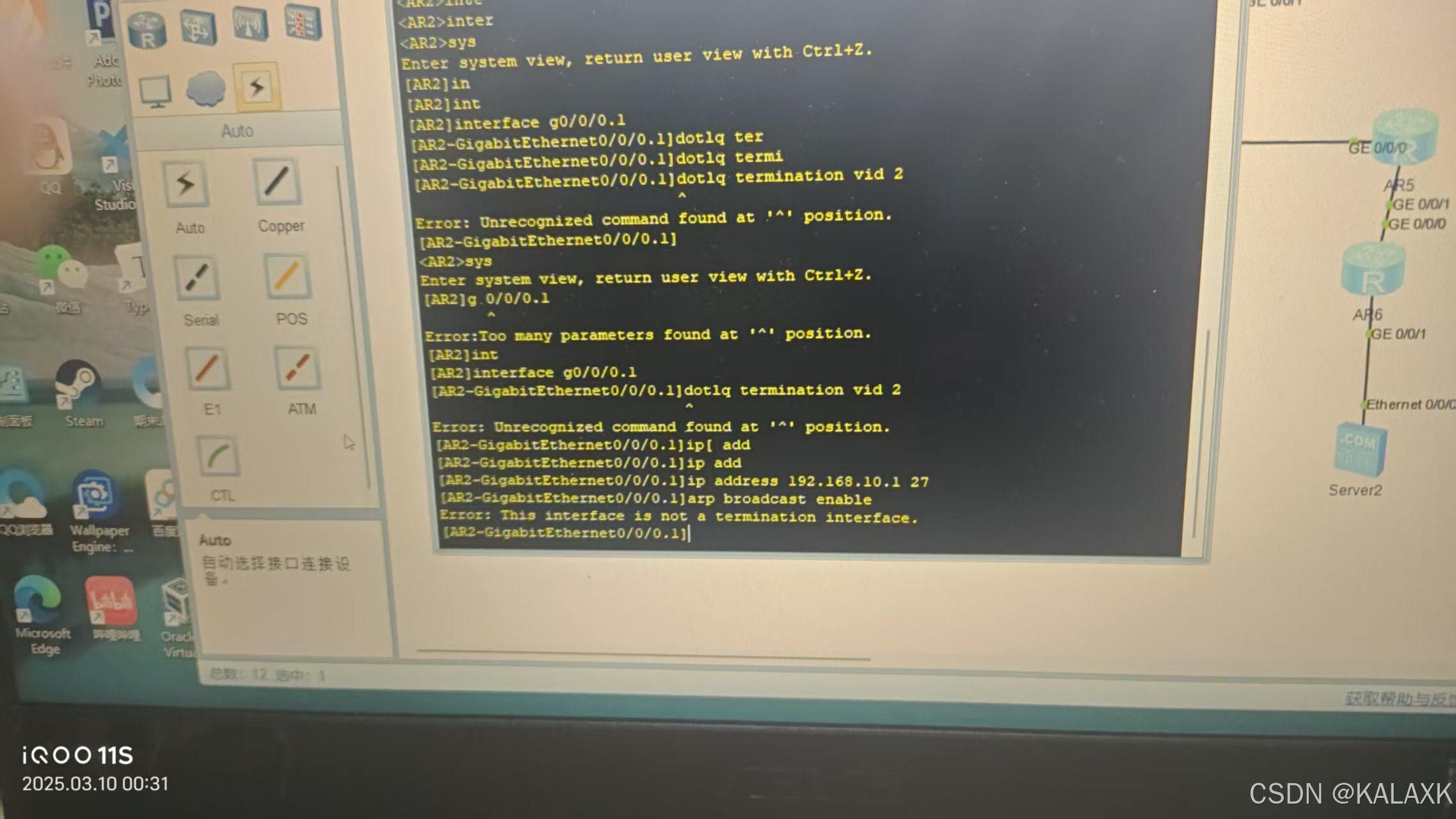
3 配置网络 交换机
1 实验图
 2 实验过程
2 实验过程
对各个路由器民命对学校网络进行基于192.168.1.0/24的子网划分,对运营商、百度网络进行基于3/3/3/0/24的子网划分,后期为满足要求,将采取配置ACL以允许PC1访问3.3.3.0/24网段,






 2 配置静态路由
2 配置静态路由

3 配置网络 交换机

 430
430
 126
126
 149
149
 2051
2051

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


