第五周 A - 最大矩形

直方图最大矩形面积算法

最新推荐文章于 2023-10-24 11:45:00 发布

原创最新推荐文章于 2023-10-24 11:45:00 发布 · 247 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#栈 #算法

本文介绍了一种高效算法，用于解决直方图中寻找最大矩形面积的问题。通过使用单调栈，该算法能在O(n)的时间复杂度内找到以每个直方图条为高度的最大矩形宽度，从而计算出最大面积。

题目描述

给一个直方图，求直方图中的最大矩形的面积。例如，下面这个图片中直方图的高度从左到右分别是2, 1, 4, 5, 1, 3, 3, 他们的宽都是1，其中最大的矩形是阴影部分。
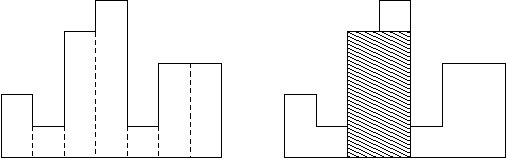
在这里插入图片描述
Input
输入包含多组数据。每组数据用一个整数n来表示直方图中小矩形的个数，你可以假定1 <= n <= 100000. 然后接下来n个整数h1, …, hn, 满足 0 <= hi <= 1000000000. 这些数字表示直方图中从左到右每个小矩形的高度，每个小矩形的宽度为1。测试数据以0结尾。

Output
对于每组测试数据输出一行一个整数表示答案。

Sample Input
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

Sample Output
8
4000

解题思路

单个矩形面积计算方法

将h1, …, hn存入数组h[100001]。要求最大矩形面积，需要对每一个h[i]求出以h[i]为高度的矩形的面积。h[i]高度已知，需要求出矩形的宽度，则需求出矩形的左边界L和右边界R的位置，即可通过公式宽度=R-L-1计算出宽度。对于h[i]，左边界为h[]中左边数第一个高度小于h[i]的元素下标+1，右边界为h[]中右边数第一个高度小于h[i]的元素下标-1。面积S=h[i]*(R-L+1)。
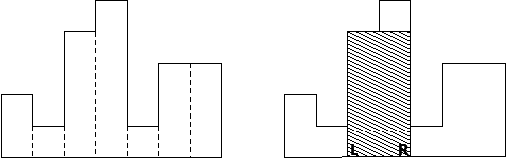
在这里插入图片描述

算法

暴力枚举（复杂度n²）

对每一个h[i]，分别往左，往右迭代找出左右边界，则时间复杂度为n²，会超时。

使用单调栈（复杂度 n)

本题使用非增栈数据结构，只需要遍历数组h[]一次就可以找到每个h[i]的左/右边界。设栈为st,栈存储的数据类型为h[i]的下标i。记录h[i]的左边界为L[i],右边界为R[i]。
右边界的寻找方法：遍历h[],从左到右依次对单调栈st进行push(i)操作，若h[i]小于栈顶元素，则弹出栈顶元素，此时，i便为栈顶元素往右数第一个小于栈顶元素的元素的下标。则栈顶元素st.top()的右边界为i-1，将这个信息记录为R[st.top()]=i-1。就这样push(i)到末尾，完成迭代后，若st内还存在元素，则这些元素的右边界为数组的末尾，即n，因此要把栈内剩余元素全部弹出，并记录下来R[st.top()]=N。此时遍历完成，h[]内所有元素均入栈一次，出栈一次，并且其右边界的下标被储存在R[]中。左边界与右边界思路一致，只是掉转了遍历的方向。使用上述方法，复杂度为n。

DEBUG

注意高度h的取值范围，需要使用long long int 来存储高度和面积，否则会出错。

代码

#include <iostream>
#include <stack> 
using namespace std; 
long long int h[100010],ans,S;
int N,L[100001],R[100001]; 

inline long long int max(long long int a,long long int b)
{
	if(a>=b) return a;
	else return b;
}

stack<int> st;

int main() {
	
	while(~scanf("%d",&N)) {
		if(N==0) break;
		ans=0;
		for(int i=1;i<=N;i++) {//输入 
 			scanf("%d",&h[i]);
 		} 
 		
 		for(int i=1;i<=N;i++) {//找右边界
 			while(!st.empty()&& h[st.top()]>h[i]) {
 				R[st.top()]=i-1;
 				st.pop();
			}
			st.push(i);
		}
		while(!st.empty()) {
			R[st.top()]=N;
 			st.pop();
		}

		for(int i=N;i>=1;i--) {	//找左边界
			while(!st.empty()&&h[st.top()]>h[i]) {
 				L[st.top()]=i+1;
 				st.pop();
			}
			st.push(i);
		}
		while(!st.empty()) {
			L[st.top()]=1;
 			st.pop();
		}
		for(int i=1;i<=N;i++) { //对每个h[i]求其矩形面积，并维护ans 
			S=h[i]*(R[i]-L[i]+1);
			ans=max(ans,S);
		}
		printf("%lld\n",ans);
	}
	return 0;
}