线性回归笔记

Regression

对数值的趋势做预测

输入为一系列相关特征值，输出我们的预测结果

1 定义一个model

即定义一个合理的function set，这里的set表示很多组参数形成的很多function，后续我们需要用梯度下降来选择最好的function

所谓Liner Model，即一个函数$f(\cdot )$可以表示成如下形式

$$f(w,b)=b+\sum w_i{x}_i$$

则我们称这样的函数为一个Liner Function.

2 定义一个loss函数，来衡量我们上面的定义的function的好坏

loss function的input是一个function，即我们的模型function，output是一个数值来表示我们上面定义的模型function多好或多不好。

$$\begin{array}{rl}\mathrm{L}(f)& =\mathrm{L}(w,b)\\ & =\sum _{n=1}^N{\left({\hat{y}}^n-\left(b+w\cdot x_{cp}^n\right)\right)}^2\end{array}$$

3 从function set中找一个最好的function

如果已经确定了方程的结构，那接下来要找一个最好的function其实就是寻找一组最优的参数$w,b$使得损失值最小：

$$f^{\ast }=arg\underset{f}{\min }L(f)$$

或者

$$\begin{array}{rl}{w}^{\ast },b^{\ast }& =\arg \underset{w,b}{\min }L(w,b)\\ & =\arg \underset{w,b}{\min }\sum _{n=1}^{10}{\left({\hat{y}}^n-\left(b+w\cdot x_{cp}^n\right)\right)}^2\end{array}$$

要解这样的方程，我们通常用梯度下降（gradient descend）方法，对于任何一个可微分方程，都可以用梯度下降来寻找最优解。（我们通常会把损失函数L处理成凸函数，这样才可以用梯度下降求得全局最优，不然只能得到局部最优。）

梯度下降指导了如何进行参数更新，至于每次更新多少，取决与：

1. 梯度下降计算的参数偏导数的值大小；
2. 一个可调节超参learning rate，一般用$\eta$来表示。

一个简单的demo，一个只有一个参数$w$的方程，来做梯度下降如下所示：

首先随机选一个初始值 $w^0$，计算方程对参数$w$的偏导数，并更新参数$w$，然后继续计算偏导数来更新参数的值，直到到达一个最优值，如下图所示：

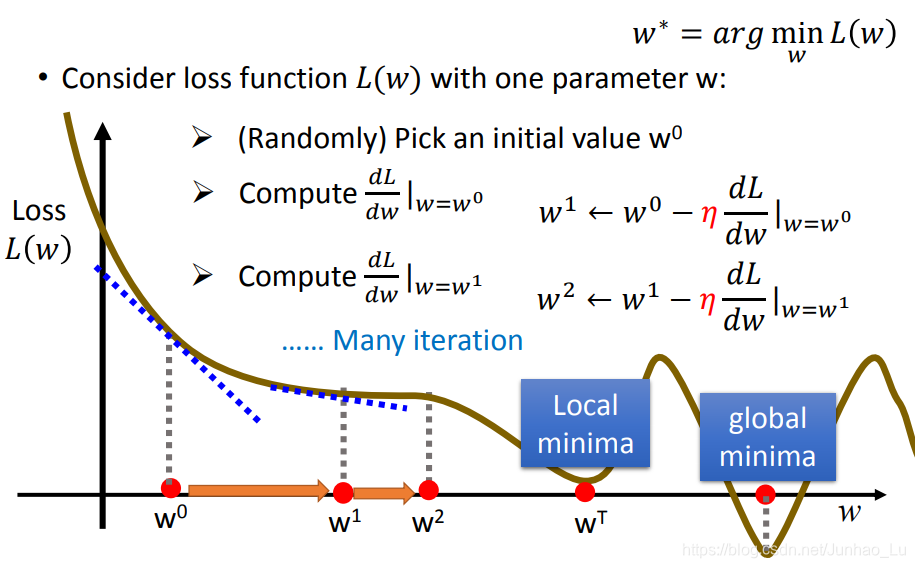
同样的，两个参数$w,b$的函数梯度下降如下：

最终，我们能得到一个使得损失值最小的最优参数值$w,b$

4 评估与优化

在训练集数据上把参数调到了最优并没有结束，我们真正关心的是该模型/函数在测试集上对新的数据的预测结果如何。

4.1 Underfitting

对于模型的性能，如果模型过于简单，一般会underfitting，即简单的模型并不能很好的拟合数据的变化趋势。

对于underfitting的情况，我们需要重新设计模型函数，增加function的复杂度，比如引入二次式，甚至三次，多次式，来更好的拟合数据（更复杂的模型同时意味着更容易过拟合）
也可以收集更多的数据特征，增加数据的信息丰富度。

4.2 Overfitting

对于复杂模型，比较容易出现过拟合的情况，原因是参数过多，function过于复杂，模型函数甚至可以拟合到训练集的每一个数据，以使损失函数L的值最小化。但造成的问题是模型不具有普适性，对于新的测试数据预测精度很差。

Overfitting的一般表现是在训练集上表现优异，准确率非常高，但在训练集上非常糟糕，准确率很低，或者训练集预测损失值有先下降后上升的趋势。

解决办法：

增大数据量：万灵丹

添加正则项：Regularization

解决过拟合问题

对于一个模型 $y=b+\sum w_i{x}_i$ 我们对其损失函数加入正则项 $\lambda \sum {\left(w_i\right)}^2$得到新的损失函数如下：

$$L=\sum _n{\left({\hat{y}}^n-\left(b+\sum w_i{x}_i^n\right)\right)}^2+\lambda \sum {\left(w_i\right)}^2$$

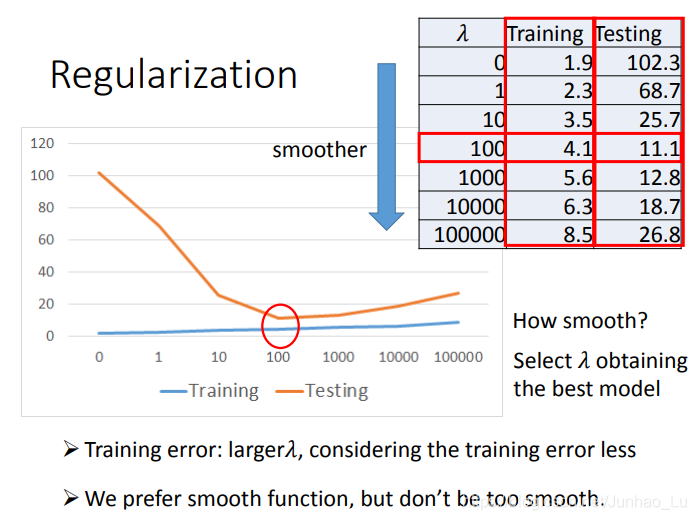
这里的正则项，就是模型方程所有参数的平方加和，乘以一个超参$\lambda$，由于我们的损失函数要取最小值，所以$\lambda \sum {\left(w_i\right)}^2$越小损失值越小，即我们期望模型方程的参数$w_i$越小越好。

为什么我需要这样的$w_i$呢，其直观意义是什么？

对于一个方程，其参数$w_i$越小，方程的曲线越平滑，即当方程的input变化时，output对input是比较不敏感的，想象极端情况下，所有的$w_i$都等于0，使$f=b$就成了一条直线，input值$x_i$再怎么边，$f$输出都不变。

使方程曲线更平滑的意义在于对输入不敏感，使得模型方程对训练数据中的一些噪音得以免疫，从而在测试集上得到更好的结果。

通常加入正则项会使训练集的损失值变大，因为他是曲线更平滑，不会过分的拟合每一个数据，但会使得测试集上的损失值更优。如下图所示：

参考李宏毅的机器学习课程做的笔记