百篇读文计划｜第四篇：BPC算法求解具有时间窗和线性权重相关成本的分集车辆路径问题

各位uu我们又见面啦！

今天在这里给大家分享一下一篇发在 informs 的 Transportaton Science 上的文章！利用 Branch-and-Price-and-Cut（BPC）解决具有时间窗和线性权重相关成本的分集车辆路径问题，文章质量非常高，建议各位看原文哦！

预计读完只需 13分钟 !

嘿嘿嘿，那我们就开始叭 ~~~

1. 前言

这篇文章介绍了一种新的车辆路径问题，涵盖了时间窗、分割配送和线性重量相关成本。这一问题是带时间窗的分割配送车辆路径问题 SDVRPTW 的扩展，考虑到车辆重量对运输成本的影响。作者们提出了精确的 Branch-and-Price-and-Cut 算法，并设计了一种新的标签设置算法来解决定价子问题。

1.1 传统车辆路径问题（VRP）

传统 VRP 是设计若干车辆行驶路线，以最小化总运输成本（通常为总行驶距离），并满足车辆容量限制、每个客户点仅访问一次以及所有路线从仓库出发并返回的约束。常见变种包括带时间窗的VRP（VRPTW）、带多仓库的VRP（MDVRP）和带分割配送的VRP（SDVRP）。解决方法包括精确算法和启发式算法。实际应用广泛，如物流配送、垃圾收集、公共交通和服务调度。这是在运筹领域和交通领域最 fundamental 的一个问题。基本很多问题都 based on VRP，就如上两篇推文的 单向汽车共享系统中的E-VReP 和 紧急停电时基站的发电机分配问题 GDP。

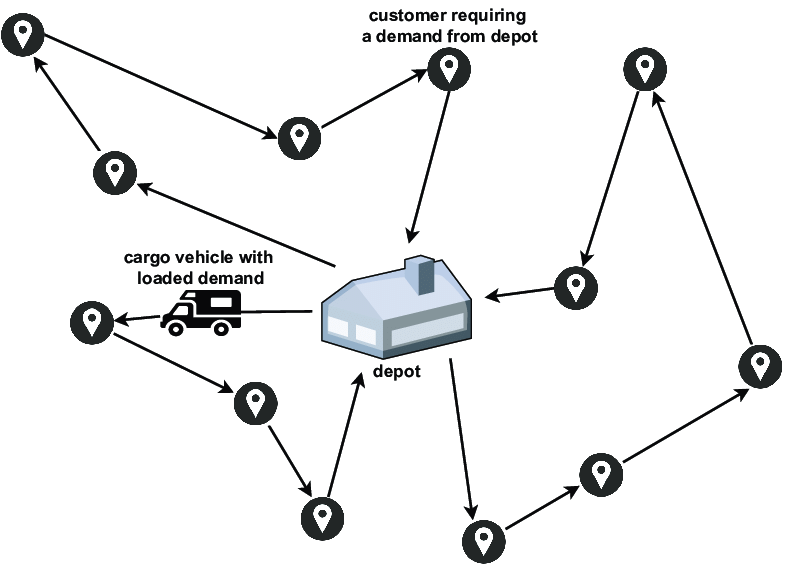
1.2 带时间窗和线性重量相关成本的分割配送车辆路径问题 SDVRPTWL

带时间窗和线性重量相关成本的分割配送车辆路径问题 the Split-Delivery Vehicle Routing Problem with Time Windows and Linear Weight-Related Cost, SDVRPTWL 是一个结合了分割配送、时间窗口和线性重量相关成本的复杂车辆路径问题模型。它允许在考虑车辆载重限制和行驶距离的基础上，灵活地规划车辆路径，以最小化总体运输成本和满足所有客户需求的约束条件。

先给大家科普一下：

分割配送车辆路径问题 Split-Delivery Vehicle Routing Problem, SDVRP

• 是车辆路径问题 VRP 的一种变体。在传统的 VRP 中，每辆车只能服务一个客户的全部需求，而在 SDVRP 中，一辆车可以在一次行程中分割配送给多个客户，从而更灵活地满足需求。

什么是分割配送？？

是指在 VRP 中的一种策略，允许一辆车在单次行程中分割配送货物给多个客户。传统的 VRP 模型假设每辆车在一次行程中只能服务一个客户的全部需求，而分割配送则放宽了这一限制，使得车辆能够更加灵活地满足多个客户的需求。

• 部分服务：车辆可以将其负载在单次行程中分割为多个部分，每个部分可以服务不同的客户需求。
• 灵活分配：这意味着在同一次行程中，车辆可以首先服务某些客户，然后回到仓库或者重新计划路径，再去服务其他客户。

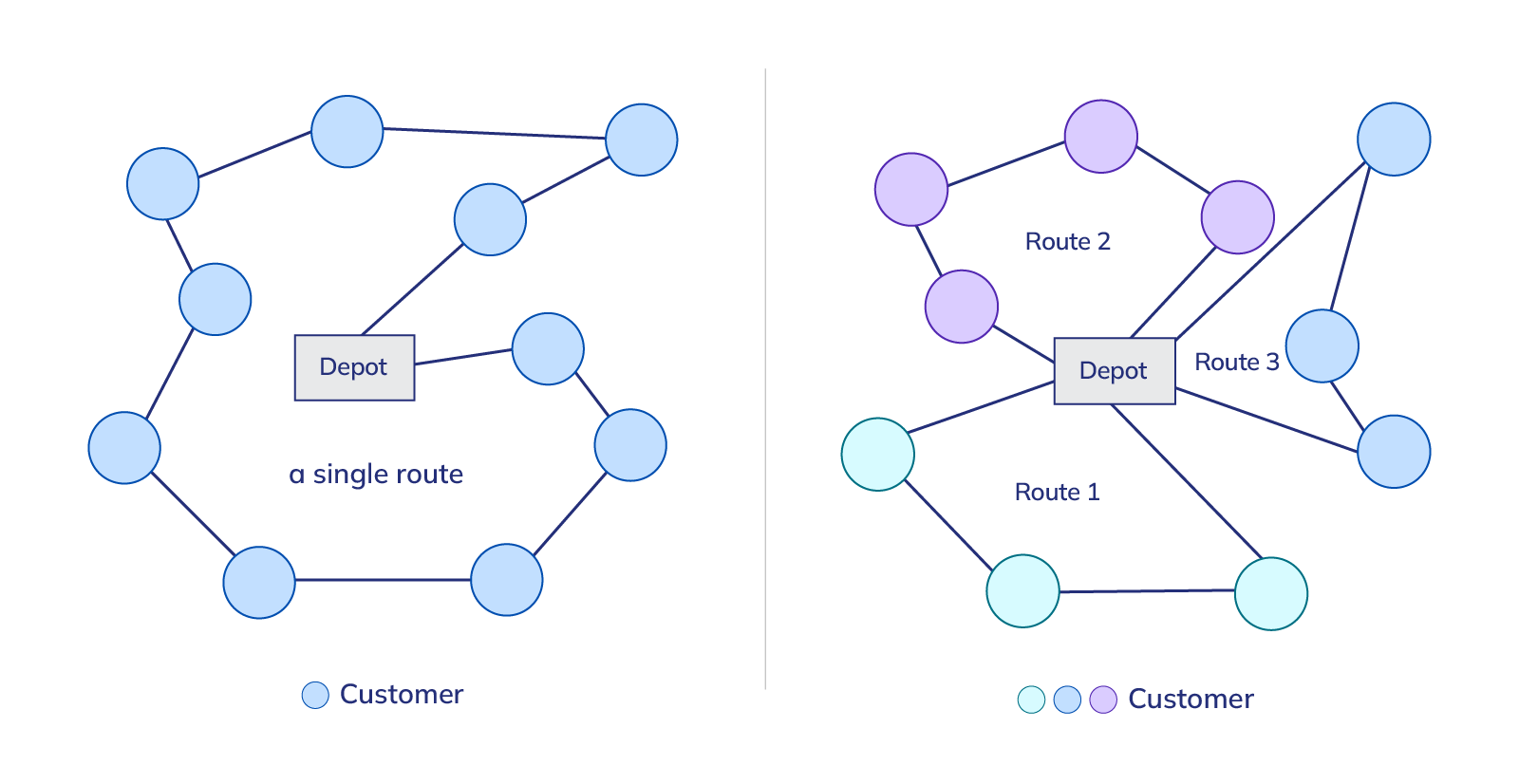
我们可以一起看看上图。如果有一辆车需要服务十个客户的需求（图左侧），传统VRP可能会规划一个完整的路线，依次经过这十个客户，并回到起点仓库。而在分割配送策略下，这辆车可以先去服务青色客户，然后回到仓库重新装载或重新规划路径，再去服务紫色和蓝色客户，甚至在这个过程中会再次回到仓库。

在这里相信uu们都已经非常清楚了❗

时间窗 Time Windows

指在车辆路径规划中，每个客户有一个指定的时间窗，在这个时间窗内必须到达客户才能被接受，以考虑客户的时间限制和服务时间。这些时间窗可以由以下两种方式定义：

• 硬时间窗 Hard Time Windows ：客户必须在指定的时间窗口内被访问，否则将被视为违规，可能会导致路径方案的不可接受。

• 软时间窗 Soft Time Windows ：客户有一个理想的时间窗口，在此期间内访问客户会有额外的成本或惩罚。虽然不是必须在此时间窗口内访问客户，但最好在此期间内访问。

给个送外卖的例子吧❗（小编最喜欢讲例子）

• 硬时间窗意味着你必须在规定的时间窗内到达客户那里。如果你迟到超过了这个时间窗，那么这次服务可能会被视为无效，客户不会接受你的服务，因为他们不再需要食物或无法等待。就是过了点我直接不要了！

• 软时间窗则表明你可以在指定的时间窗外到达客户那里，但是每迟到一定时间会有额外的成本。这种成本可以通过扣除你的小费或公司给你的奖金来体现，也可以是客户不再愿意使用你的服务。就是过了点没关系，可是你必须要被扣钱！

线性重量相关成本 Linear Weight-Related Cost

• 在 SDVRPTWL 中，考虑了车辆载重对运输成本的影响，采用了线性重量相关成本模型。
• 成本函数 $f(w)$ ：假设运输成本不仅与行驶距离相关，还与车辆的载重 $w$ 相关。具体地，成本函数可以表示为 $f(w)=a\times w+b$，其中 $a$ 和 $b$ 是常数，$w$ 是车辆的载重。$a$ 表示了每增加单位重量所增加的额外成本；$b$ 表示了空载（或基本成本）情况下的运输成本。
• 这意味着随着车辆的载重增加，单位距离的运输成本也会相应增加。例如，当车辆携带更多货物时，可能需要更多的燃料，而这种额外的燃料消耗会增加成本。

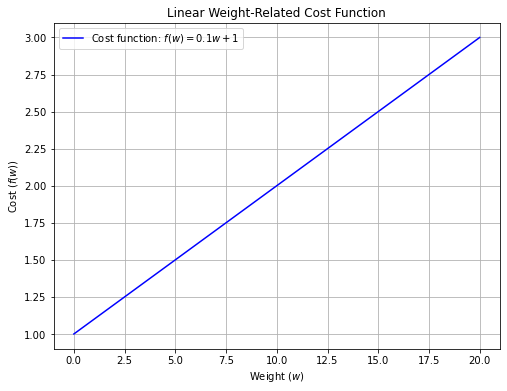
为了让大家更直观明白，我这里假设 $a=0.1$ 和 $b=1$ ，然后画出成本函数的图形，展示成本随着车辆重量增加而线性增加的情况，可以看到 $x$ 轴是车辆重量
$w$ ，$y$ 轴是对应的运输成本 $f(w)$。

关键核心问题

在这里就会有几个问题我们需要思考一下：

1. 如何考虑成本模型的准确性和实用性，以及在实际运输中其他因素（如燃料价格变化、道路条件等）的影响呢？
2. 如何有效地在时间窗口内规划路径，以最小化总运输成本呢？
3. 如何合理分配车辆容量以满足所有客户的需求，并在此过程中优化运输成本呢？

以上的问题，大家一起想一想哈~~~

---

2. 问题描述

SDVRPTWL 定义在一个有向图 $G=(V,E)$ 上，其中 V={0,1,…,n+1}V = \{0, 1, \ldots, n+1\}V={0,1,…,n+1} 是顶点集合，$E=\{(i,j)\mid i,j\in V,i\ne j,i\ne n+1,j\ne 0\}$ 是边集 。其中顶点 $0$ 和 $n+1$ 分别是出口和入口到仓库的点，其余顶点 VC={1,…,n}V_C = \{1, \ldots, n\}VC​={1,…,n} 是顾客集合。

1. 符号定义：

• $d_0=+\infty$ ：表示仓库顶点 $0$ 的需求为无穷大，即仓库不需要接受产品。
• $d_{n+1}=0$ ：表示入口顶点 $n+1$ 的需求为零，即仓库不需要提供产品。
• $s_0=s_{n+1}=0$ ：表示仓库顶点 $0$ 和入口顶点 $n+1$ 的服务时间为零。
• $e_0=e_{n+1}=0$ ：表示仓库顶点 $0$ 和入口顶点 $n+1$ 的时间窗口起始时间为零。
• $l_0=l_{n+1}=+\infty$ ：表示仓库顶点 $0$ 和入口顶点 $n+1$ 的时间窗口结束时间为无穷大，即没有限制。

2. 边的属性：

• $(i,j)\in E$ ：表示图 $G$ 中存在一条从顶点 $i$ 到顶点 $j$ 的边。
• $c_{i,j}\ge 0$ ：表示边 $(i,j)$ 的距离非负。
• $t_{i,j}\ge 0$ ：表示边 $(i,j)$ 的遍历时间非负。
• 三角不等式保证了对于任意三个顶点 $i,j,k$ ，有 $c_{i,j}\le c_{i,k}+c_{k,j}$ 和 $t_{i,j}\le t_{i,k}+t_{k,j}$ ，即从一个顶点到另一个顶点的最短路径满足三角形式。

3. 顶点的后继和前驱：

• V+(i)={j∈V∣ei+si+ti,j≤lj,(i,j)∈E}V^+(i) = \{ j \in V \mid e_i + s_i + t_{i,j} \leq l_j, (i, j) \in E \}V+(i)={j∈V∣ei​+si​+ti,j​≤lj​,(i,j)∈E} ：顶点 ( i ) 的后继顶点集合，满足时间窗口约束。
• V−(i)={j∈V∣ej+sj+tj,i≤li,(j,i)∈E}V^-(i) = \{ j \in V \mid e_j + s_j + t_{j,i} \leq l_i, (j, i) \in E \}V−(i)={j∈V∣ej​+sj​+tj,i​≤li​,(j,i)∈E} ：顶点 $i$ 的前驱顶点集合，满足时间窗口约束。
• 每个顶点 $i$ 有正的需求 $d_i$，服务时间 $s_i$ ，和一个时间窗 $[e_i,l_i]$ 表示服务可以开始的时间范围。
• 每条边 $(i,j)\in E$ 有非负距离 $c_{i,j}$ 和穿越时间 $t_{i,j}$，并满足三角不等式。

4. 车辆和配送模式：

• 每辆车具有相同的重量容量 $Q$ 。
• 每辆车从仓库顶点 $0$ 出发，访问一些顾客，每个顾客处交付一定数量的产品，最后返回入口顶点 $n+1$ 。
• 每个配送模式定义了一条路线，指定了每个顶点交付的产品数量。
• 如果车辆在顶点 $i$ 处早于时间窗 $e_i$ 到达，它必须等到时间窗开始后才能开始服务。

5. 配送模式的可行性：

• 一个配送模式是可行的，如果其路线尊重所有访问顾客的时间窗口，并且其总交付需求不超过 $Q$。
• 每个顾客的需求可以由多辆车满足，即顾客需求可能大于车辆容量，并且可以多次访问同一顾客。

6. 边的遍历成本：

• 边 $(i,j)$ 上的遍历成本由承载重量 $w_{i,j}$ 的车辆支付，计算公式为 $c_{i,j}\times f(w_{i,j})$ ，其中 $f(w_{i,j})=a\times w_{i,j}+b$ ，且 $b$ 是车辆的基本成本。

7. 优化目标：

• SDVRPTWL 的目标是找到一组可行的配送模式，以满足所有顾客的需求，并且使总遍历成本最小化。

问题的性质

1. 性质 1：存在一个最优解，其中每条路线最多只访问每个顾客一次。
2. 性质 2：最优解中，最多只有一辆车可以被分配到有两个或更多客户的路线
3. 性质 3：每条边 $(i,j)\in E_C$ 最多只出现一次，其中 $E_C=\{(i,j)\mid (i,j)\in E,i,j\in V_C\}$。

参数变量

1. 参数：

• K={1,2,…,m}K = \{1, 2, \ldots, m\}K={1,2,…,m} ：表示可用车辆的集合，总数为 $m$ 辆。
• $M$ ：表示一个足够大的正数，通常用于表示无穷大或非常大的上界。

2. 决策变量：

• $x_{i,j,k}$ ：二进制变量，如果车辆 $k$ 能够穿越边 $(i,j)$ ，则取值为 $1$ ，否则为 $0$ 。
• $w_{i,j,k}$ ：车辆 $k$ 在边 $(i,j)$ 上的负载重量。
• $a_{i,k}$：车辆 $k$ 在顾客 $i$ 处的服务开始时间。

目标函数

min⁡∑k∈K∑i∈VC∪{0}∑j∈V+(i)ci,j(awi,j,k+bxi,j,k)\min \sum_{k \in K} \sum_{i \in V_C \cup \{0\}} \sum_{j \in V^+(i)} c_{i,j}(a w_{i,j,k} + b x_{i,j,k})mink∈K∑​i∈VC​∪{0}∑​j∈V+(i)∑​ci,j​(awi,j,k​+bxi,j,k​)

• $K$ 是可用车辆的集合。
• $V_C$ 是顾客的集合。
• $V^{+}(i)$ 是顶点 $i$ 的后继顶点集合。
• $c_{i,j}$ 是从顶点 $i$ 到顶点 $j$ 的距离或成本。
• $w_{i,j,k}$ 是车辆 $k$ 在边 $(i,j)$ 上的负载重量。
• $x_{i,j,k}$ 是二进制变量，如果车辆 $k$ 穿越边 $(i, j) $，则为 $1$ ；否则为 $0$ 。
• $a$ 和 $b$ 是常数，其中 $b$ 表示车辆的固定成本。

它目的是寻找一组可行的配送模式，使得所有顾客的需求得到满足，并且考虑到负载重量和固定成本 $b$，使总的遍历成本最小化。

详细约束请阅读原文。

经过了问题描述，不知道大家都理解透了吗 ~~~

---

3. 算法流程

3.1 Dantzig–Wolfe 分解

Dantzig–Wolfe 分解是将问题分解为主问题和定价子问题来处理的数学分解技术，其中主问题包含与每条路径兼容的所有交付模式的决策变量。为了求解主问题，使用了 Column Generation 算法，并通过 Branch-and-Price-and-Cut 算法来处理整个问题。定价子问题则通过定制的标签设置算法来解决。

• **原问题（SDVRPTWL）**的变量被分组，其中每组变量代表一种特定的交付模式或路径。
• 分解后得到的主问题负责决定哪些路径和交付模式应该被使用，以及它们应该被使用多少次。
• 定价子问题用于生成新的列（即新的路径或交付模式），这些列被逐步加入到主问题中，以改进当前的解。

主问题MP的构建

• 目标函数：最小化总运输成本，这由不同路径和交付模式的成本之和表示。
  $$z^{MP}=\min \sum _{r\in R}\sum _{p\in P_r}{c}_{r,p}{\theta }_{r,p}$$
  其中，$c_{r,p}$ 表示路径 $r$ 下的模式 $p$ 的成本，${\theta }_{r,p}$ 表示模式 $p$ 被分配的车辆数量。

• 约束条件：

  • 客户需求：确保每个客户的需求都能被满足。
    $$\sum _{r\in R}\sum _{p\in P_r}{\delta }_{i,p}{\theta }_{r,p}\ge d_i\forall i\in VC$$
    其中，${\delta }_{i,p}$ 表示在模式 $p$ 下在客户 $i$ 处交付的数量，$d_i$ 表示客户 $i$ 的需求量。

  • 车辆容量：确保任何路径上的货物总量不超过车辆的容量。
    $$\sum _{r\in R}\sum _{p\in P_r}{\alpha }_{r,p}{\theta }_{r,p}\ge \lceil \frac{d_i}{Q}\rceil \forall i\in VC$$
    其中，$Q$ 为车辆的容量。

为什么不直接把这一块扔给 CPLEX 处理啊？因为由于路径和交付模式的数量庞大，即使是简单的实例，主问题的变量数量也非常大，所以无法直接使用 CPLEX 处理。

定价子问题

• 定价子问题用于在当前主问题线性松弛问题求解得到的对偶变量的基础上，寻找具有最小 reduced cost 的路径和交付模式。

• 它实际上是一个带资源限制的最短路径问题 ESPPRC（NP-complete），即在资源约束条件下，寻找通过图的最短路径。

• 目标函数：
  $${\bar{c}}_{r,p}=c_{r,p}-\sum _{i\in r}\left({\delta }_{i,p}{\pi }_i+{\mu }_i\right)$$
  其中，${\pi }_i$ 和 ${\sigma }_i$ 是与客户需求和车辆容量约束相关的对偶变量。

---

以上只是一个小科普，让大家可以理解一下基本概念，那阅读文章的时候就可以更加通透了。

---

3.2 列生成 CG 及其定价子问题

列生成方法用于解决具有大量变量的大规模线性规划问题。这种方法通过逐步引入对优化目标函数和约束有关键影响的列（变量），来避免直接求解主问题 MP，从而提高求解效率。

1. 受限主问题（RLMP）：

   • RLMP的定义：RLMP 是主问题 MP 的一个简化版本，包含的变量是定价子问题生成的少数列，而不是所有可能的列。由于 RLMP 的变量数量相对较少，因此可以通过标准的单纯形算法高效地求解。
   • RLMP的解及对偶变量：求解 RLMP 可以得到一组当前的最优解和相应的对偶变量值。这些对偶变量值将在接下来的定价子问题中起关键作用。

2. 定价子问题：

   • 定价子问题的目标：定价子问题的核心是找到新的列，这些列对当前 RLMP 的解具有改进作用，即具有负的 reduced cost。
   • 定价子问题的解法：定价子问题的求解过程涉及枚举所有可能的配送模式，也就是 CG 中的列，计算它们的reduced cost。如果发现负的 reduced cost 的列，则引入 RLMP，并开始新的列生成迭代；否则，列生成过程终止，当前 RLMP 的解即为主问题 MP 的最优解。

极端配送模式 Extreme Delivery Pattern

极端配送模式的定义：

• 极端配送模式是一种特殊的配送模式，其中每个客户节点的配送量要么为0（即不配送），要么为满载配送（即达到需求量），要么仅对一个节点进行部分配送。这种模式是所有可能配送模式的极端情况。
• 这种模式的引入是基于一种理论，即定价子问题的最优解中至少存在一个极端配送模式。所以文中只考虑极端配送模式来简化定价子问题的求解过程。

极值配送模式的证明（文中定理3）：

• 文中定理3证明了，定价子问题的最优解中至少存在一个是极端配送模式。这意味着在求解定价子问题时，只需在所有可能的极端配送模式中寻找最优解，从而大幅减少了搜索空间。

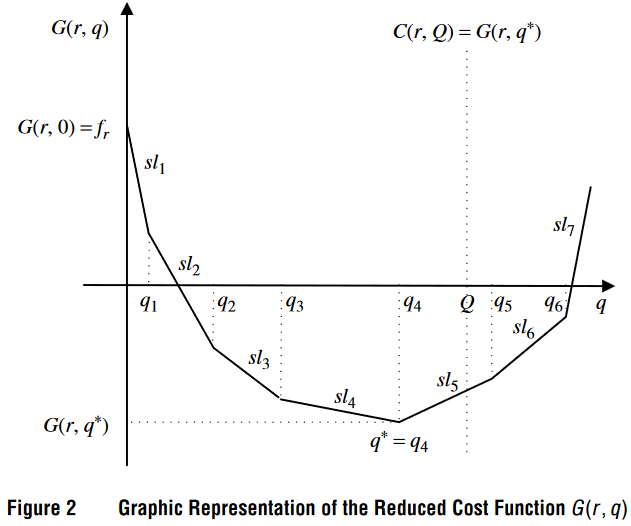
文中有个函数非常重要，这个函数 $G(r,q)$ 用来表示在特定的路径 $r$ 上，配送量 $q$ 对应的最小化 reduced cost。

• 凸性：显然函数 $G(r,q)$ 是凸的，意味着随着配送量 $q$ 的增加，函数的值变化呈现出一个非递减的模式。具体来说，初始时 reduced cost 的降低幅度较大，但随着配送量的增加，reduced cost 的边际效益逐渐减小。

• 连续分段线性：函数 $G(r,q)$ 是由多个线性段组成的，且这些线性段在某些点（即每个节点的需求量）发生转折。每个线性段的斜率由节点的边际效益 $g_{v_k^{\prime }}$ 决定，较高的边际效益对应较陡的斜率。

• 函数 $G(r,0)=f_r$: 在 $q=0$ 时，函数值等于固定成本 $f_r$，这表示在没有任何配送量的情况下，路径 $r$ 的固定成本。

• 斜率 $s{l}_k=-g_{v_k^{\prime }}$: 每一段的斜率等于负的节点边际效益 $-g_{v_k^{\prime }}$，这是因为在增加配送量时，reduced cost 的速率由边际效益决定。

• 节点需求量 $q_k$: 每个节点的需求量 $q_k$ 是函数 $G(r,q)$ 转折点的横坐标，对应的是前 $k$ 个节点的累积需求量。

那这里的 $C(r,Q)$ 应该怎么计算？

• 从 $G(r,q)$ 中获取 $C(r,Q)$: 通过函数 $G(r,q)$ 的最小值，计算出路径 $r$ 对应的最小化减少成本 $C(r,Q)$，即 $C(r,Q)=G(r,q^{\ast })$，其中 $q^{\ast }$ 是在 $[0,Q]$ 范围内使 $G(r,q)$ 最小的配送量。

• 零配送量的条件: 如果节点的边际效益 $g_{v_i} $ 小于等于零，那么对应的配送量 ${\delta }_{v_i}$ 会被设为零。也就是说，如果给定路径 $r$ 上的某个节点在当前解中没有产生任何收益（即其 $g_{v_i}\le 0$），就不需要将任何配送量分配到该节点。

3.3 标签设置算法

标签设置算法是一种广泛使用的技术，用于解决各种车辆路径规划模型的定价子问题。解决定价子问题的目标是确定具有负的 reduced cost 的完整路径，即 $C(r,Q)$。在我们的标签设置算法中，定义了一个多维标签 $E_i=({\tau }_i,N_i,V_i,G(r,q),F_i,S{L}_i,I_i)$，它表示与从顶点 0 到顶点 i 的可行（部分）路径 r 相关的状态，其中：

• ${\tau }_i$ 是在顶点 i 的最早服务开始时间，必须在 $[e_i,l_i]$ 内；
• $N_i\subseteq V$ 是所有已访问顶点的集合；
• $V_i\subseteq V$ 是从路径 r 可以到达的所有顶点的集合；

标签的扩展

在顶点 0 处，定义初始标签 $E_0=({\tau }_0,N_0,V_0,G(r,q),F_0,S{L}_0,I_0)$ 为：

• ${\tau }_0=0$
• N0={0}N_0 = \{0\}N0​={0}
• $V_0=V$
• $G(r,q)$ 是与路径 $r$ 和配送容量 $q$ 相关的最小减缩成本
• $F_0$, $S{L}_0$, $I_0$ 为初始值

每个顶点可以有多个标签，通过扩展标签到顶点 $j\in V$ 生成新的标签 $E_j$。扩展函数包括：

• ${\tau }_j=\max (e_j,{\tau }_i+s_i+t_{i,j})$
• Nj=Ni∪{j}N_j = N_i \cup \{j\}Nj​=Ni​∪{j}
• Vj=Vi−{k∈V+(j):τj+sj+tj,k>lk}−{j}V_j = V_i - \{k \in V^+ (j) : \tau_j + s_j + t_{j,k} > l_k\} - \{j\}Vj​=Vi​−{k∈V+(j):τj​+sj​+tj,k​>lk​}−{j}
• $F_j=F_i+b{c}_{i,j}-{\mu }_j$
• SLj=SLi∪{gj}SL_j = SL_i \cup \{g_j\}SLj​=SLi​∪{gj​}
• Ij=Ii∪{dj}I_j = I_i \cup \{d_j\}Ij​=Ii​∪{dj​}

---

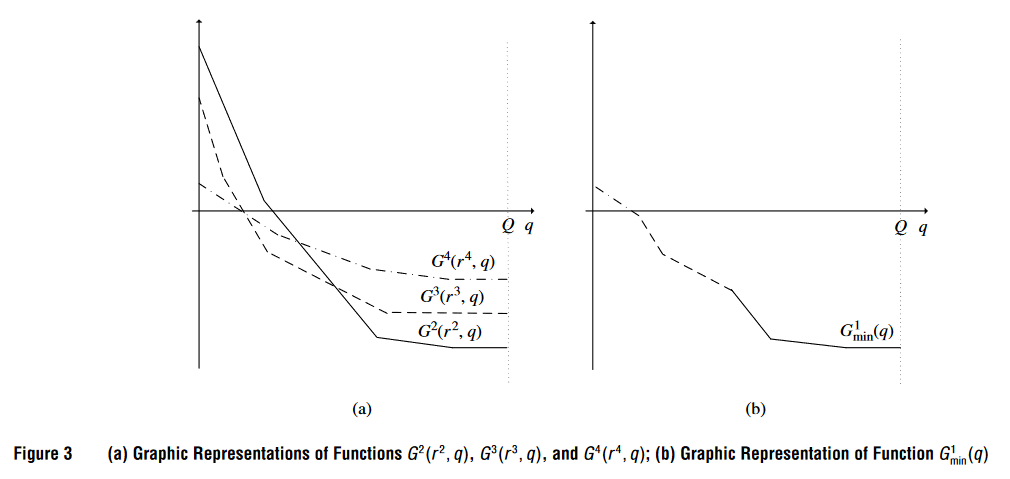
上图展示了从多个简化成本函数中选取的最小简化成本函数 $G_{min}^1(q)$。该函数由所有相关标号的简化成本函数的最小部分组成，并且不一定是凸的。上图也在说明一种新的支配规则，即集合支配规则（Set Dominance Rule）。我们可以看到虽然一个标号不能被其他单个标号支配，但可能会被一组标号的联合支配。这个图帮助解释如何利用所有相关标号的信息来构建一个新的最小简化成本函数，并通过这种方法安全地丢弃被支配的标号，从而优化算法的性能。

文中给出了集合支配规则的例子

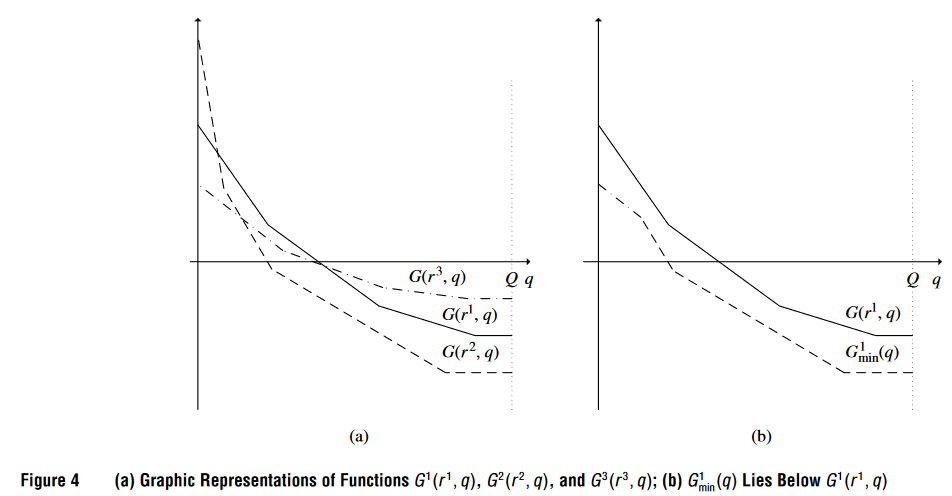
上图说明如何通过集合支配规则来支配标号。图中展示了两个标号 $E_2^i$ 和 $E_3^i$，尽管它们单独都不能支配标号 $E_1^i$，但它们的联合却可以支配 $E_1^i$。这个图也展示了集合支配规则比传统的配对支配规则更为强大，能够更有效地减少待处理的标号数量，进而提升算法的效率。

---

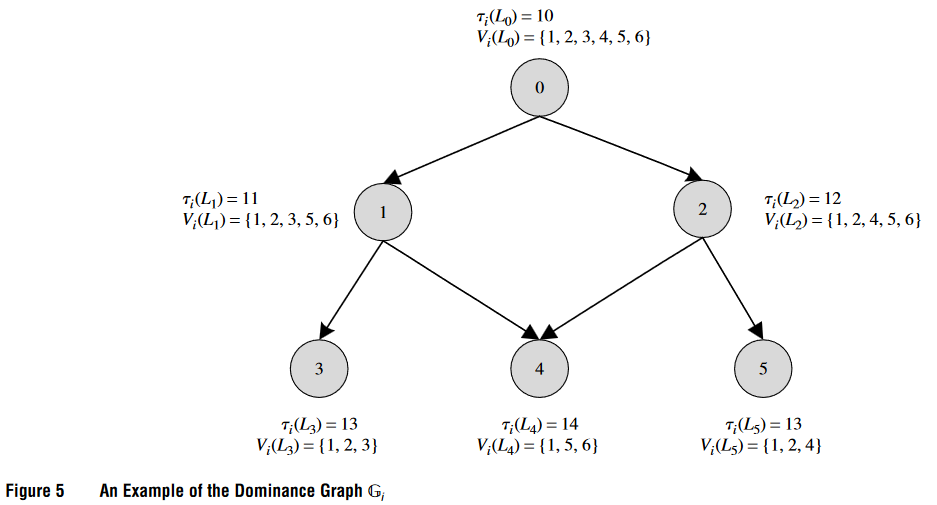
上图就展示了支配图的一个例子。在这个图中，节点表示终止于同一顶点的非支配标号集合。图中还显示了这些节点之间的有向边，边的创建是基于特定的条件，如最早服务开始时间和可达顶点集合等。这个图也详细展示了如何从根节点开始更新支配图，从而消除支配标号。

在算法运行过程中，支配图用于跟踪和维护非支配标号，并且通过添加新标号或调整最小简化成本函数来不断更新，从而优化标号设定算法的整体性能。

详细的算法加速策略建议大家阅读原文哈！

---

❗ ❗不要因为看到复杂的数学符号就怕了不敢读下去，其实他只是个符号，跟我们平时用的 $x$ 和 $y$ 是一样的❗ 读到这里已经很棒了，还有一半，加油❗❗

---

这段文字介绍了在带时间窗的集成配送问题（SDVRPTWL）中使用的有效不等式，以及如何将这些不等式应用到标签设定算法中。以下是对这部分内容的详细整理和分析：

3.4 有效不等式

$k$-路径不等式

定义：

• $k$-路径不等式 是用来限制每条路径上必须覆盖一定数量的客户。形式为：
  $$\sum _{r\in R}\sum _{p\in P_r}\sum _{(i,j)\in E^{-}(S)}{\beta }_{i,j,r}{\theta }_{r,p}\ge \lceil \frac{{\sum }_{i\in S}{d}_i}{Q}\rceil \forall S\in \Gamma$$

• 左边：

  • ${\sum }_{r\in R}$：对所有的路径 $r$ 求和。
  • ${\sum }_{p\in P_r}$：对每条路径 $r$ 中的每个模式 $p$ 求和。
  • ${\sum }_{(i,j)\in E^{-}(S)}$：对离开客户子集 $S$ 的所有边 $(i,j)$ 求和。
  • ${\beta }_{i,j,r}$：表示边 $(i,j)$ 是否在路径 $r$ 中使用的二进制参数。
  • ${\theta }_{r,p}$：表示模式 $p$ 是否在路径 $r$ 中使用的二进制参数。

• 右边：

  • $\lceil \frac{{\sum }_{i\in S}{d}_i}{Q}\rceil$：表示客户子集 $S$ 的需求总和与车辆容量 $Q$ 之比的上取整值。这表示需要的车辆数量。

这个不等式的作用是确保对于每个客户子集 $S$，至少有足够的路径覆盖从 $S$ 中离开的边，从而满足总需求所需的车辆数量。这是为了保证在解中满足路径规划的合理性，确保不会因为边覆盖不足而违反容量约束。

强最小车辆数不等式 Strong Minimum Number of Vehicles (SMV) Inequalities.

定义：

• SMV 不等式 旨在控制车辆数量，通过以下不等式实现：
  $$\sum _{r\in R}\sum _{p\in P_r}\left(2{\alpha }_{i,r,p}^F+{\alpha }_{i,r,p}^{SZ}\right){\theta }_{r,p}\ge 2\forall i\in V_S$$

• 左边：

  • ${\sum }_{r\in R}$：对所有的路径 $r$ 求和。
  • ${\sum }_{p\in P_r}$：对每条路径 $r$ 中的每个模式 $p$ 求和。
  • $2{\alpha }_{i,r,p}^F+{\alpha }_{i,r,p}^{SZ}$：其中：
  • ${\alpha }_{i,r,p}^F$ 是二进制参数，表示如果客户 $i$ 在路径 $r$ 的模式 $p$ 中进行了完整交付（Full Delivery），则 ${\alpha }_{i,r,p}^F=1$，否则为 0。
  • ${\alpha }_{i,r,p}^{SZ}$ 是二进制参数，表示如果客户 $i$ 在路径 $r$ 的模式 $p$ 中进行了拆分交付（Split Delivery）或零交付（Zero Delivery），则 ${\alpha }_{i,r,p}^{SZ}=1$，否则为 0。
  • ${\theta }_{r,p}$：表示模式 $p$ 是否在路径 $r$ 中使用的二进制参数。

• 右边：

  • $2$：表示每个客户 $i$ 在客户集合 $V_S$ 中至少需要的车辆数。

---

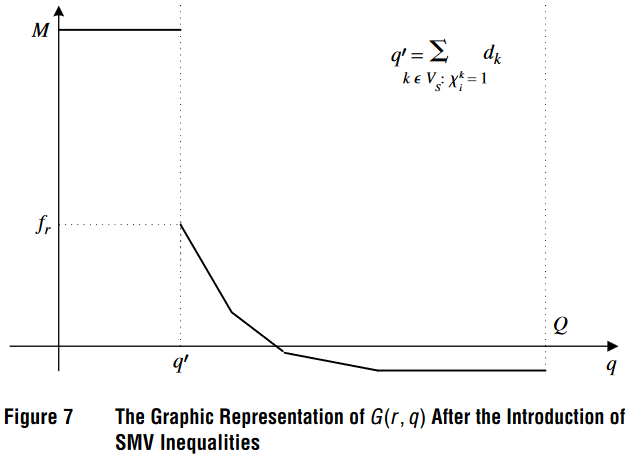
在考虑SMV 不等式时，上图展示在引入这些不等式后的图形结构和处理方式，这样的表示有助于理解如何在实际图中应用这些不等式以及如何调整路径搜索算法。

搜索策略

• 使用 最优优先策略（best-first policy）来探索分支定界树。
• 深度优先策略 在初步实验中结果不如最优优先策略。

分支策略

• 在每个分支定界节点上，通过列生成程序和分离启发式方法求解 LMP 的最优解，并将其作为下界。
• 分支策略:
  • 总车辆数
  • 每个客户的车辆数
  • 每条边的总流量
  • 包括或不包括两个连续的边

我们来个简单整理：

• $k$-路径不等式 和 SMV 不等式 用于改进带时间窗的集成配送问题的解决方案，通过调整标签设定算法和简化成本函数。

• 搜索策略 和 分支策略 确保在求解过程中尽可能高效地找到最优解。
  由于路径集合 $R$ 过于庞大，直接求解 SF 是不切实际的。为了解决这一问题，文中采用了 CG 算法，它是一种迭代过程，交替求解 SF 公式的线性规划 LP 松弛问题和定价子问题。

• 通过松弛约束，允许 $0\le {\theta }_r\le 1$（对于每个 ${\theta }_r\in R$），从而得到线性主问题 LMP 。然后，通过选择初始列的集合 $\Omega \subseteq R$，得到受限线性主问题 RLMP ，并在每次迭代中更新该集合。CG 方法的目的是在每次迭代中找到负的reduced cost，并将它们纳入 RLMP。当找不到这样的列时，过程终止。如果 CG 结束时的线性解是可行的，那么它对于 LMP 和 RLMP 都是最优的。

• 每个 RLMP 的解都有对应的对偶解，这些对偶值在 reduced cost 函数中起到关键作用，用于更新路径集合 $\Omega$。通常，BPC 过程从一组初始列开始，为标签设置算法后续迭代提供上限。在这个情况下，即使 $\Omega =\varnothing$ ，SF 仍然是可行的，这意味着在解决定价子问题之前不需要生成初始列。

---

这里比较复杂，涉及的技术比较多，可能需要大家多看几次才会理解清楚哦（我也看了不止一次。。。）

---

4. 算法优势

实例

作者们使用了Solomon（1987）提出的56个基准VRPTW实例，这些实例分为六个组：R1、C1、RC1、R2、C2和RC2。每个Solomon实例包含一个仓库和100个客户，总共101个顶点。我们从这些100客户的实例中派生出了25客户和50客户的实例，总共形成504个实例，分为54组。每个实例组的标识符由Solomon实例组的名称、客户数量 n 和车辆容量 Q 组成。例如，实例组R1-100-30包含n = 100和Q = 30的R1组实例。距离被四舍五入到小数点后一位。权重相关成本函数为 $f(w)=a\times w+b$，其中 $a=1$ 和 $b=Q/4$。

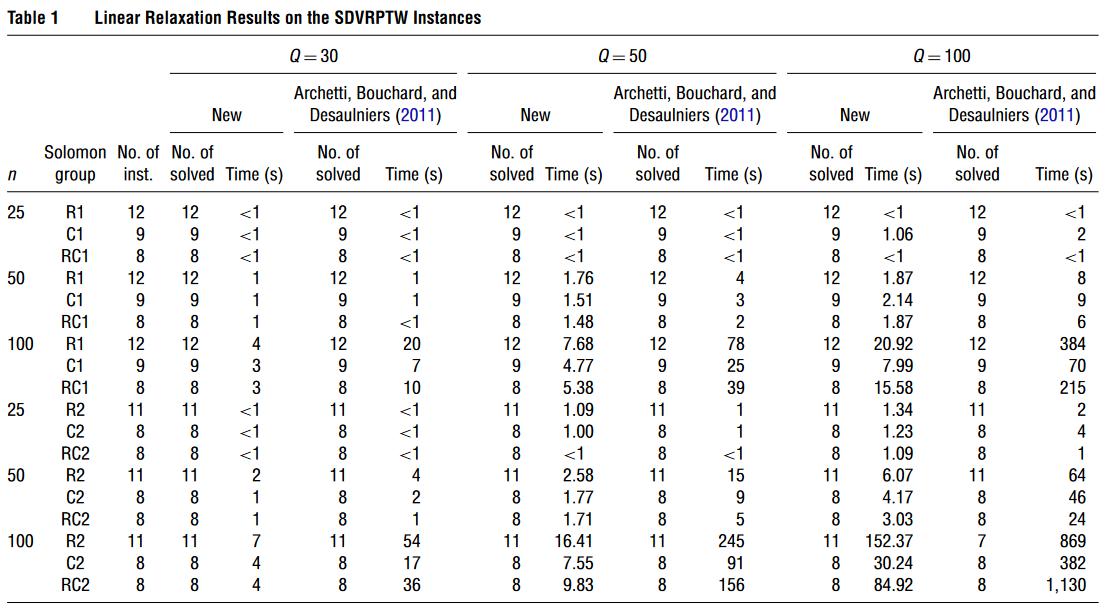
SDVRPTWL 实例的结果

作者们将 BPC 算法应用于所有 SDVRPTWL 实例，这些实例的距离矩阵经过了满足三角不等式的更新。

在算法开始时，他们解决了包含所有 n 个 SMV 不等式但不考虑 $k$-path不等式的 MP 的线性松弛。

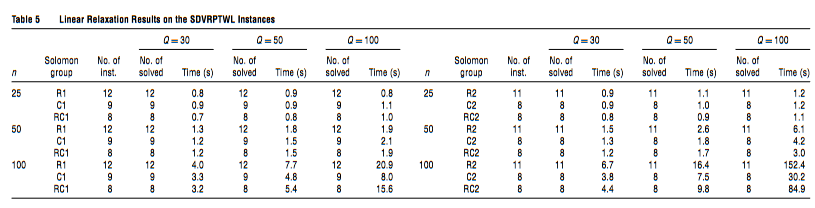
$Table5$ 中报告了线性松弛的结果，表明为每个实例达到了下界。

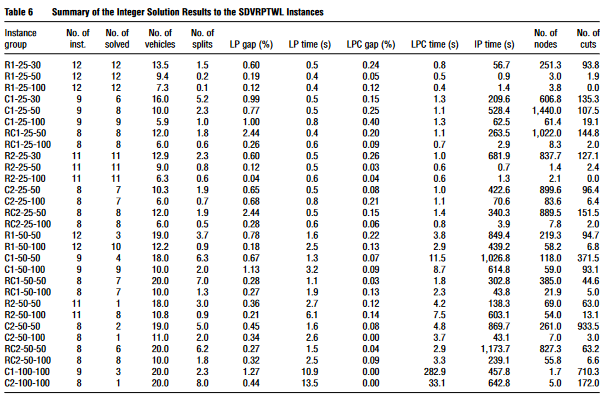
$Table6$ 总结了SDVRPTWL实例的整数解结果。得出作者们设计的算法成功解决了504个SDVRPTWL实例中的208个，其中138个、66个和4个实例包含25、50和100个客户。

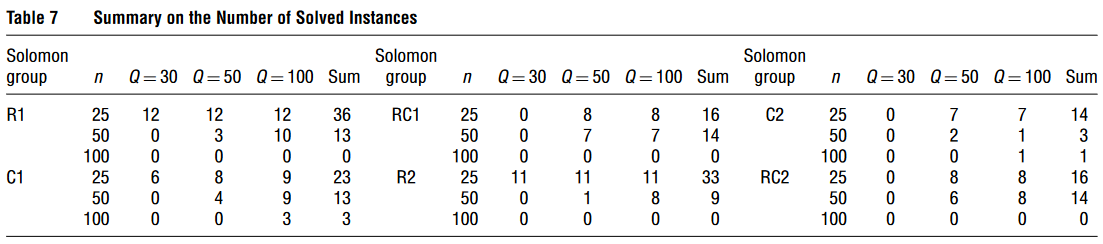
$Table7$ 展示了各实例组中最优解实例的数量。

按照上述结果，非常显然，这个 BPC 算法表现非常好。

1. 计算效率：

   • SDVRPTW 实例：算法在SDVRPTW实例中表现出较短的计算时间，尤其是在分支定价剪枝算法的根节点解决LMP时，比之前的方法（如Archetti、Bouchard及Desaulniers（2011））平均计算时间显著更短。
   • SDVRPTWL 实例：算法同样成功解决了208个SDVRPTWL实例，其中许多实例在更短的时间内得到了最优解。

2. 准确性：

   • SDVRPTW 实例：算法在所有测试实例的根节点成功找到了 LMP 的最优解。相较于Archetti、Bouchard及Desaulniers（2011）的方法，算法解决了更多的实例，并且能够找到在一些情况下没有被报告的最优解。
   • SDVRPTWL 实例：该算法还成功解决了208个 SDVRPTWL 实例，显示了较强的准确性和可靠性。

3. 方法对比：

   • 在列生成程序的比较中，使用 AGH 列生成器的CG1程序比Archetti的标签扩展算法表现更好。
   • 双向搜索的有效性也得到了验证，进一步提升了算法的性能。

4. 实例分类：

   • 算法在解决不同类别的实例中表现优异，包括那些之前未能找到最优解的实例。

---

怎么样？是不是很神奇呢？哈哈哈哈哈是的，这也许就是我们喜欢研究这个领域的原因~~~这一篇 TS 的文章真的真的真的十分强大！！！喜欢算法设计的人必看！！！

今天的分享到这里结束咯。不知道你看明白了吗 ~~~

（看得懂或看不懂的小伙伴记得点赞收藏慢慢看多几次哦）

---

参考文献：

原论文：
Luo, Z., Qin, H., Zhu, W., & Lim, A. (2017). Branch and price and cut for the split-delivery vehicle routing problem with time windows and linear weight-related cost. Transportation Science, 51(2), 668-687.