几种常见的二叉树

几种常见的二叉树

1. 满二叉树

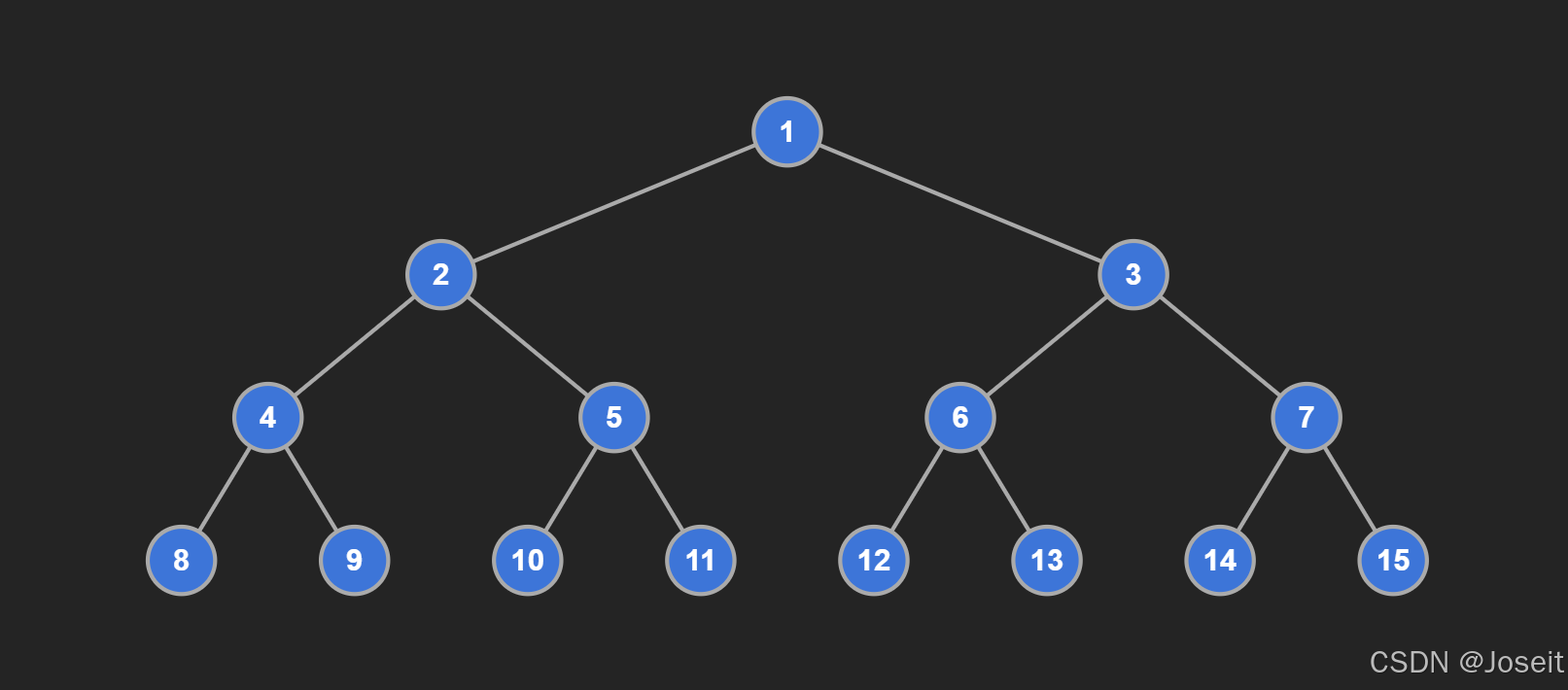
看图比较直观，满二叉树每一层节点都是满的，整棵树像一个整的三角形，其有一个优势，就是树的节点比较好算，设 整个整棵树的高度为：h ，那节点的个数为：2^h - 1 。使用等比求和公式即可。

2. 完全二叉树

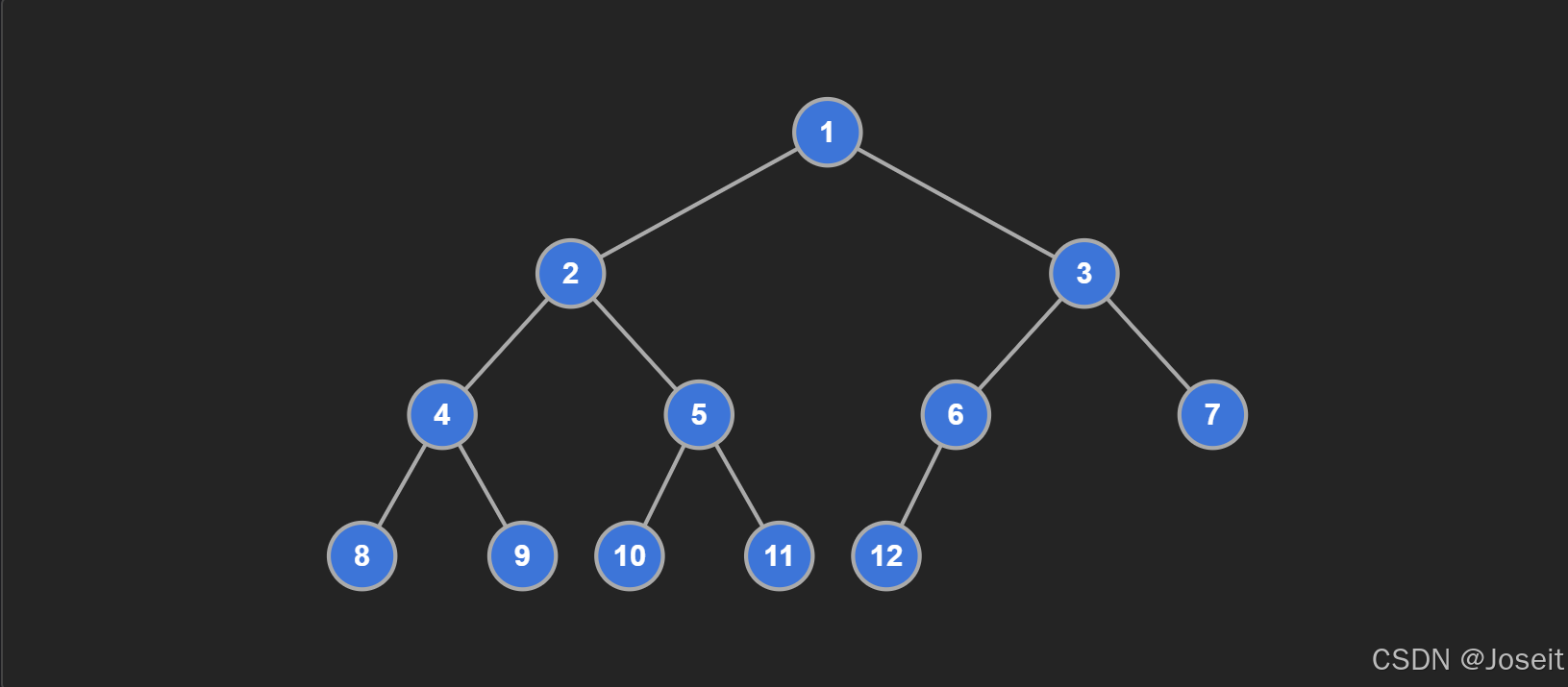
完全二叉树指的是：左边的节点一定是紧凑挨着的，除了最后一层节点，其他层的节点都是满的。

完全二叉树的特定：由于它的节点是紧凑排列的，假如从左到右，从上到下给每个节点进行编号，会发现父子节点的索引存在明显的规律。

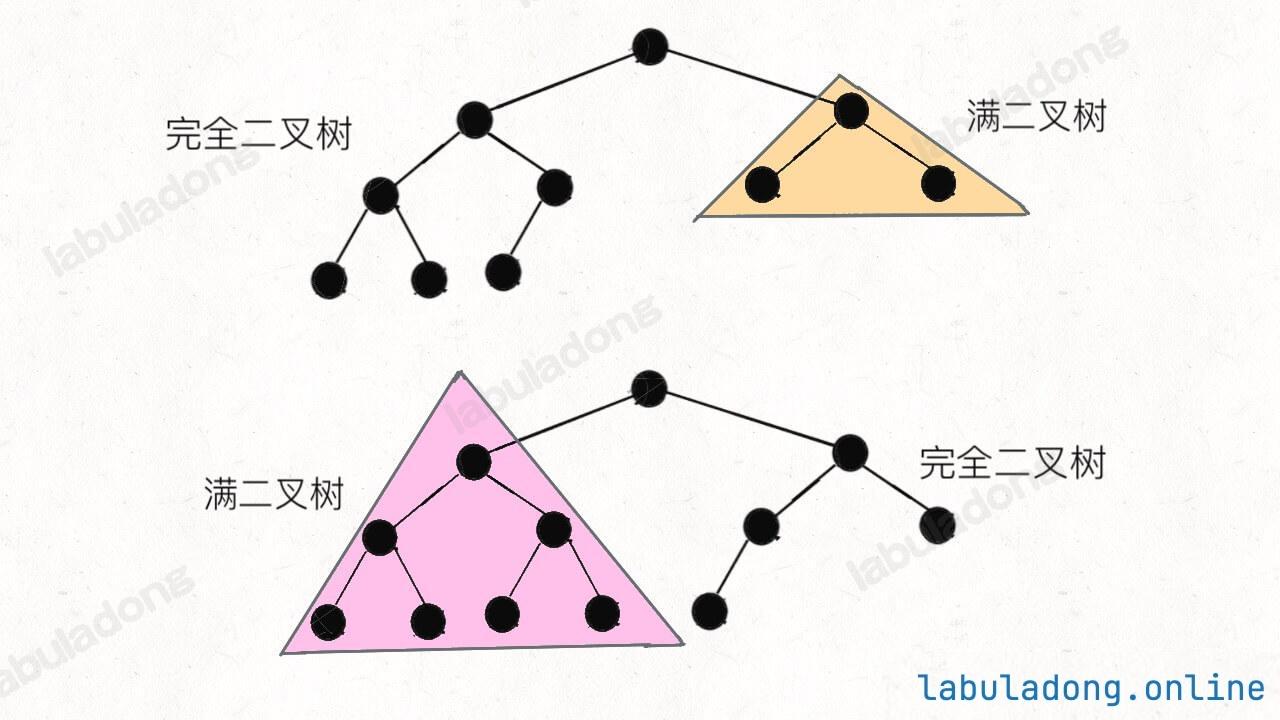
完全二叉树还有一个不明显的特点：完全二叉树的左右子树都是完全二叉树，换句话说，完全二叉树左右子树中，有一棵一定是满二叉树。

3. 二叉搜索树

对于每个二叉搜索树（Binary Search Tree，简称 BST）来讲，它的左子树的每个节点的值都小于这个节点的值，它的右子树的每个节点的值都大于这个节点的值。可以记作：【左小右大】

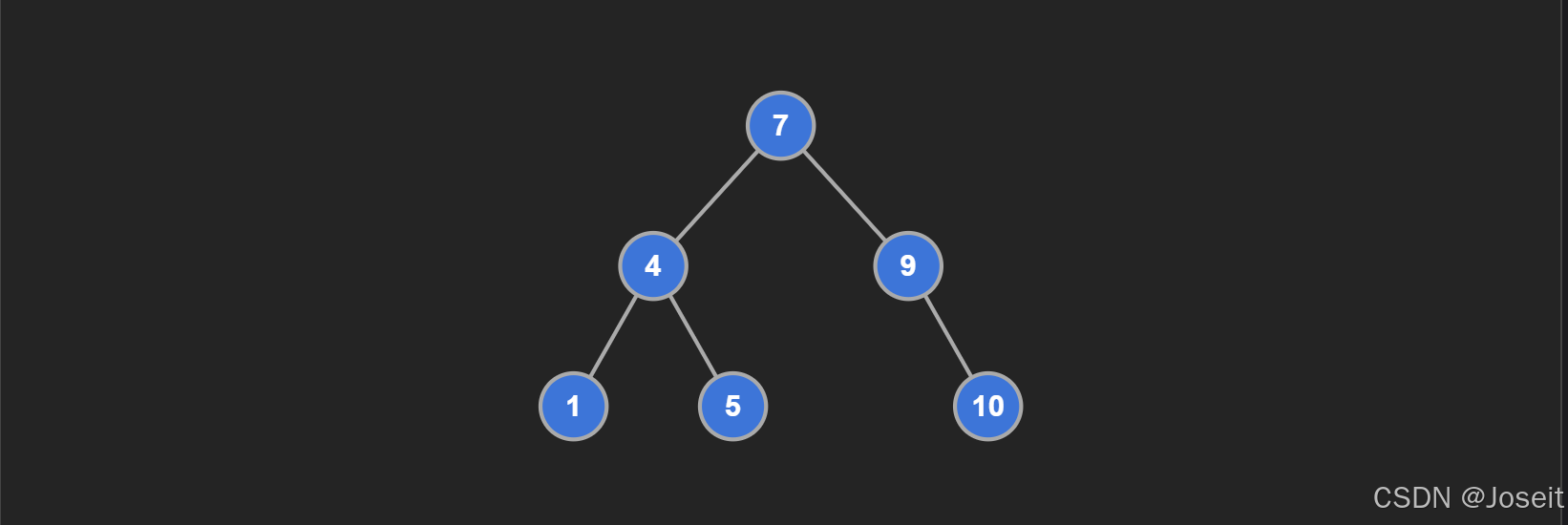
这就是一棵二叉搜索树，随便找个节点 4 ，它的左子树的节点 1 小于 4，而它的右子树的节点 5 就比 4大。相反，下面这棵就不是二叉搜索树。

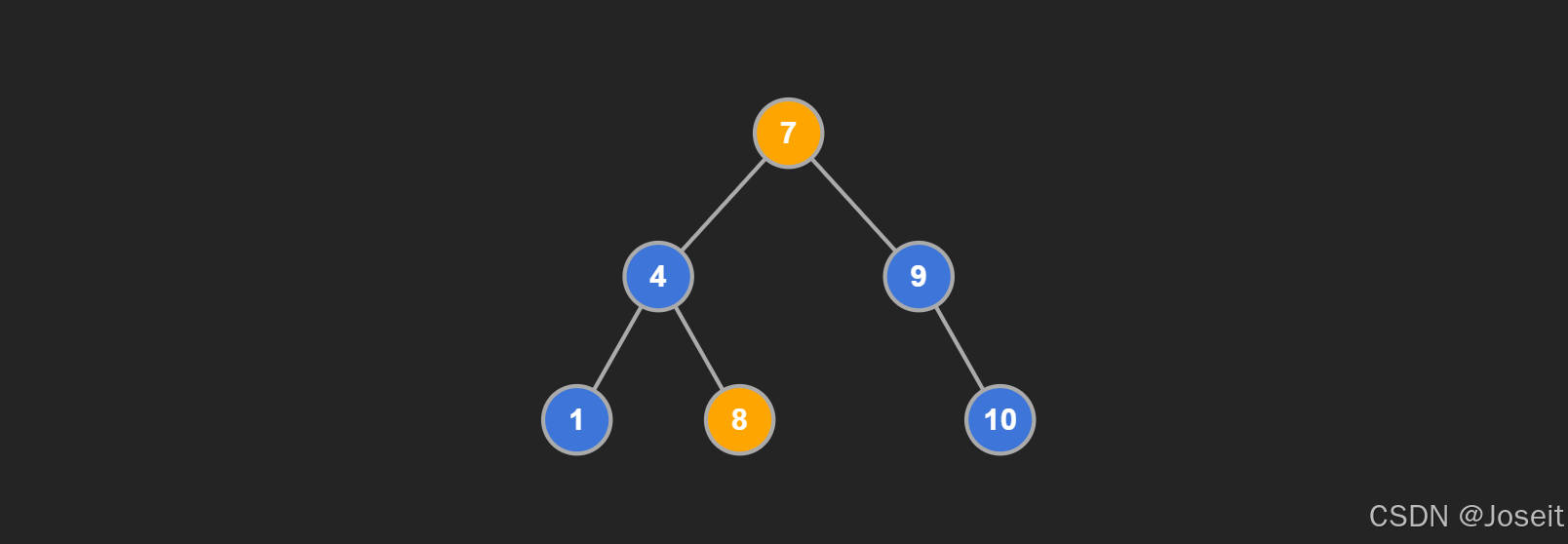
你看，节点 7 的左边就不遵从【左小右大】的原则，所以这棵不是二叉搜索树。

BST 是很常用的数据结构，因其【左小右大】的特性，可以用于快速排查元素的位置。用上面第一张图来举个例子，假如你想找 9 这个节点，可以直接根据根节点 7 左小右大的特性，直接把左子树排查掉，直接从右子树开始，这样搜索的效率提高了。

4. 高度平衡二叉树

高度平衡二叉树（Height-Balanced Binary Tree）是一种特殊的二叉树，特点是：它的【每个节点】的左右子树的高度差不超过 1 。要注意，是每个节点，不是特指根节点。

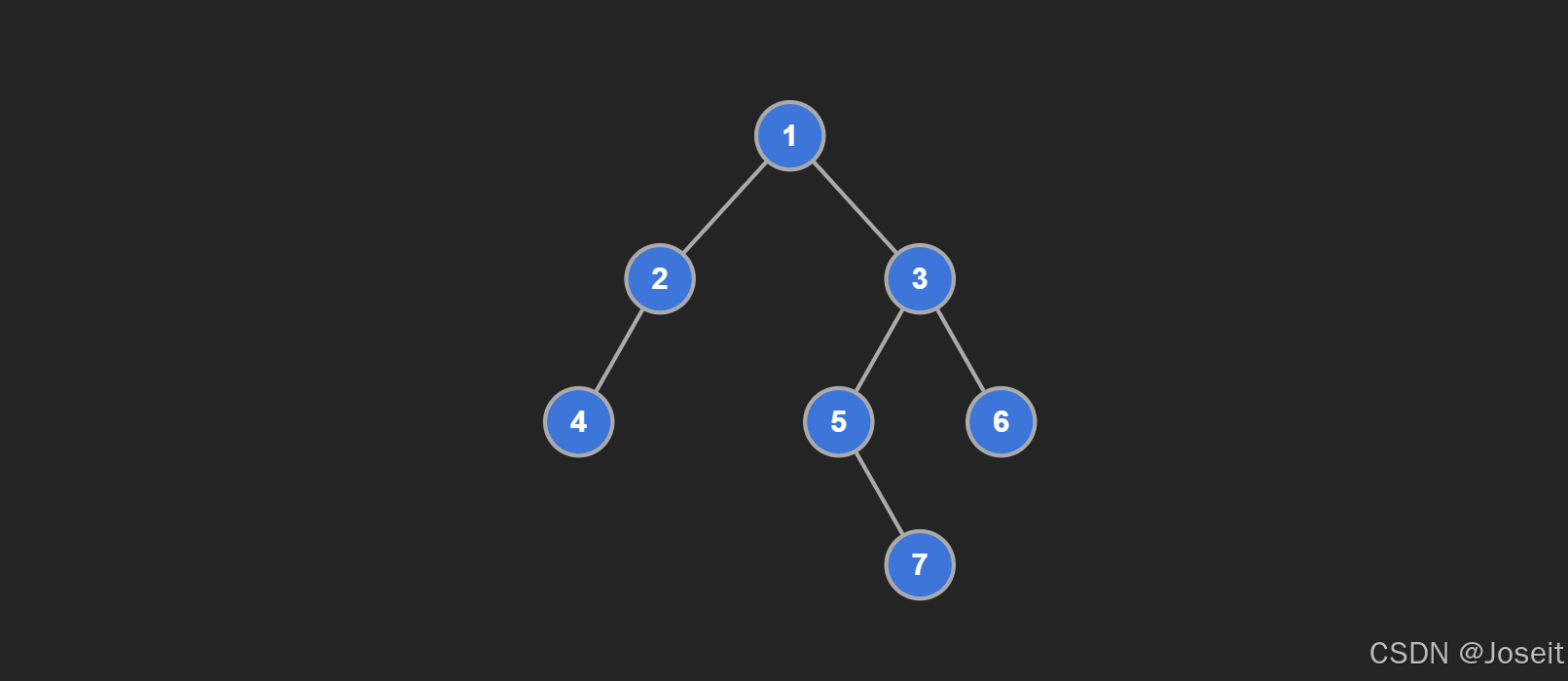
例如上面这棵二叉树，根节点 1 的左子树高度是 2，右子树高度是 3；节点 2 的左子树高度是 1，右子树高度是 0；节点 3 的左子树高度是 2，右子树高度是 1，以此类推，每个节点的左右子树高度差都不超过 1，所以这是一棵高度平衡的二叉树。下面这棵就不是高度平衡的二叉树：节点 2 的左子树的高度是 2 而右子树的高度是 0 很明显不符合左右子树的高度差不超过 1 的特性。

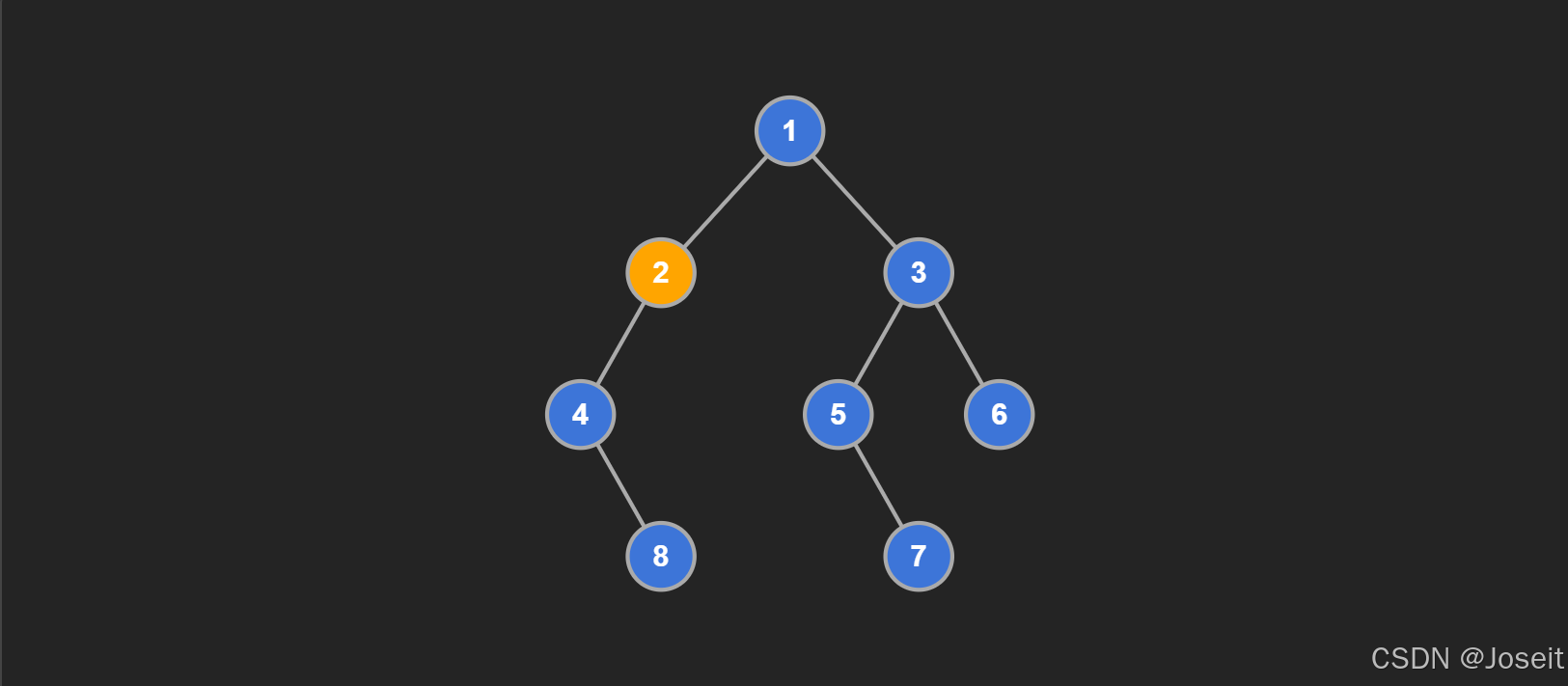
假设高度平衡二叉树中有 N 个节点，那么高度平衡二叉树的高度是：O(log(N))，这是非常重要的性质，如果能保证二叉树的高度为：O(log N) ，数据结构的增删改查的效率就会大幅度提高。

5. 二叉树的实现

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    public TreeNode(int x) {this.val = x};
}
// 你可以这样构建一棵二叉树：
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.right.left = new TreeNode(5);
root.right.right = new TreeNode(6);
// 构建出来的二叉树是这样的：
//     1
//    / \
//   2   3
//  /   / \
// 4   5   6

在一般的算法中，我们把实际的问题抽象成二叉树结构，但我们不需要使用 TreeNode 来创建一个二叉树，而是直接使用类似于哈希表的结构来表示二叉树 / 多叉树。

比如这棵二叉树，我可以使用一个哈希表，其中使用键 key 来表示父节点 id ，值 value 来表示子节点的列表（每个节点的 id 是唯一的），那么一个键值对就表示一个多叉树的节点。

// 1 -> [2, 3]
// 2 -> [4]
// 3 -> [5, 6]

HashMap<Integer, List<Integer>> tree = new HashMap<>();
tree.put(1, Arrays.asList(2, 3));
tree.put(2, Collections.singletonList(4));
tree.put(3, Arrays.asList(5, 6));

这样就能够模拟一个二叉树或多叉树的结构。