假设检验

要理解假设检验，就要从概率分布图讲起。如下概率分布图：

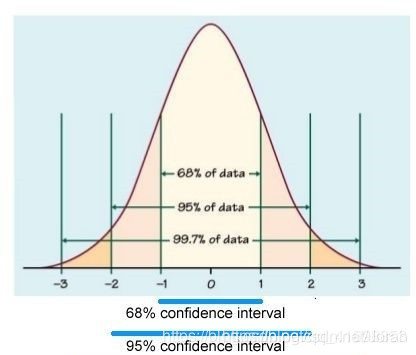
这个图如何理解呢？

它的横轴是样本的取值，它的纵轴是相应取值出现的概率。

比如最简单的：扔骰子，它的概率分布图就是6个高度一样的点，因为1点到6点它们出现的概率都一样，都是16.7%（100%／6）。

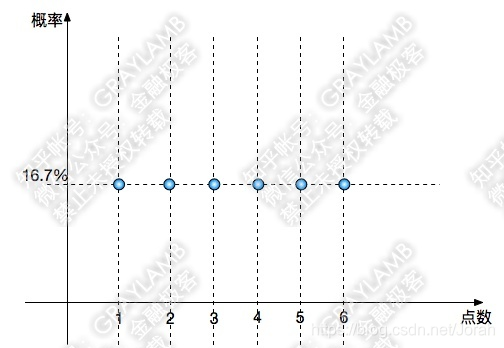
一般假设检验采用“置信区间法”或者“检验统计量”去检验。

1）采用“置信区间”：其实上面的例子就使用的“置信区间”进行检验。但在实际使用中，会先确定一个小概率事件的概率范围。比如，上面例子中，我把“小概率”定义为1%；我也可以把“小概率”定义为2%、 5%、10%。那相应也就越来越容易拒绝原假设了：

假设检验的逻辑是是什么？

如果“小概率”是1%，那么落在红色的区域拒绝，拒绝难度比较大。

假设检验的逻辑是是什么？

如果“小概率”是5%，那么红色的区域变大了，落在红色区域的可能性也变大了，更容易拒绝原假设了。

这个人为定的“小概率”，我们给起了一个名字叫做“显著性水平”。而红色区域有个名字，叫做“拒绝域”。

“拒绝域”没有覆盖到的区域，叫做“置信区间”，它其实是抛去“拒绝域”概率所剩的概率，如果“拒绝域”的概率是5%，那么“置信区间”的概率就是95%（如上图红色区域和白色区域）。可以简单理解为95%的情况下，我都相信原假设成立（所以95%是“置信”区间），一旦出现那5%的小概率事件，我就认为原假设不成立。

2）采用“检验统计量”：

检验统计量（又叫：标准化统计量）的公式为：