快速幂算法入门：5分钟掌握核心思想

原创于 2025-12-13 10:24:09 发布 · 529 阅读

CC 4.0 BY-SA版权

输入框内输入如下内容：

生成一个讲解快速幂算法的教学代码，要求代码简单易懂，附带详细的注释和分步说明。使用Python语言实现，并通过几个简单的例子展示算法的执行过程。

示例图片

最近在学习算法时，遇到了快速幂这个概念。一开始看到这个名词有点懵，但经过一番研究后，发现它的思想其实非常简单易懂。今天就来分享一下我的学习心得，希望能帮助到同样在学习算法的朋友们。

快速幂是一种高效计算幂运算的算法。比如我们要计算a的n次方，最直观的方法就是用循环连续乘n次。但当n很大时，这种方法的效率就很低了。快速幂通过分治的思想，将时间复杂度从O(n)降低到O(logn)。

快速幂的核心在于将指数n进行二进制分解。具体来说： 1. 将指数n表示为二进制形式 2. 利用幂的乘法性质，将大问题分解为小问题 3. 通过不断平方的方式，将计算复杂度降低

举个例子，计算3的13次方： 1. 13的二进制是1101 2. 可以表示为3^8 * 3^4 * 3^1 3. 通过平方的方式快速计算出3^1,3^2,3^4,3^8等

在Python中实现快速幂非常简单： 1. 初始化结果为1 2. 当指数大于0时循环 3. 如果当前位是1，就乘上对应的幂 4. 每次循环将底数平方，指数右移一位

让我们看几个例子来理解快速幂的执行过程： 1. 计算2^10：只需要4次乘法 2. 计算5^7：只需要4次乘法 3. 计算10^6：只需要6次乘法

相比普通的循环乘法，快速幂在指数较大时优势非常明显。比如计算2^100，普通方法需要100次乘法，而快速幂只需要7次。

快速幂在很多领域都有应用： 1. 密码学中的模幂运算 2. 大数计算 3. 矩阵快速幂

特别是当我们需要计算大数的幂时，快速幂几乎是必不可少的算法。

对于初学者来说，理解快速幂可以分几步： 1. 先理解二进制表示 2. 掌握幂的乘法性质 3. 通过小例子手动计算 4. 最后再看代码实现

这样循序渐进，就能很好地掌握这个算法了。

最近我在InsCode(快马)平台上实践这个算法时，发现它的编辑器非常方便，可以实时看到代码运行结果。特别是对于算法学习来说，能够快速验证自己的想法是否正确。

示例图片

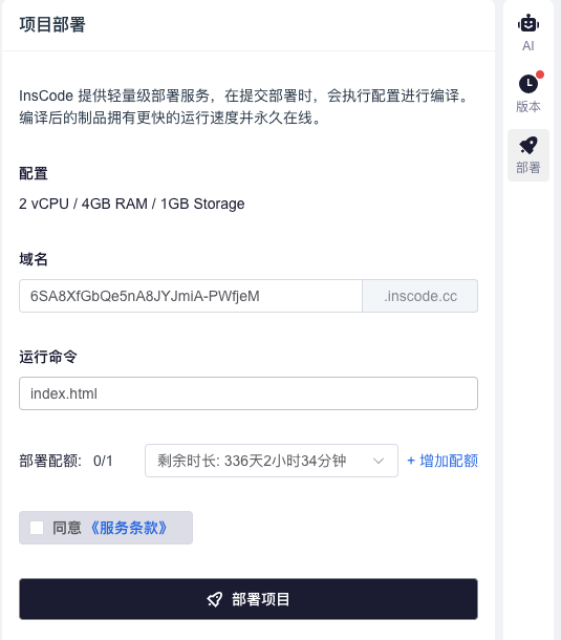
平台还支持一键部署功能，虽然快速幂这种算法演示不太需要部署，但对于其他需要持续运行的项目来说，这个功能真的很实用。

示例图片

总的来说，快速幂是一个既简单又强大的算法，掌握了它对我们理解其他复杂算法也很有帮助。希望这篇文章能帮到正在学习算法的你！

输入框内输入如下内容：

生成一个讲解快速幂算法的教学代码，要求代码简单易懂，附带详细的注释和分步说明。使用Python语言实现，并通过几个简单的例子展示算法的执行过程。

创作声明：本文部分内容由AI辅助生成（AIGC），仅供参考